Escolhemos programação por restrição por encontrar uma boa solução rapidamente e que aceite mudanças com facilidade.
A solução foi adaptada de uma solução de escala de enfermeiras (vide links) que consiste em preencher uma matriz solução como esta:
| Nome | t1 | t2 | t3 | t4 | |
| 1 | Calouro1 | DEP | DEP | DEP | DEP |
| 2 | Calouro2 | DEP | DEP | DEP | DEP |
| 3 | Calouro3 | DEP | DEP | DEP | DEP |
| 4 | Calouro4 | DEP | DEP | DEP | DEP |
| 5 | Calouro5 | DEP | DEP | DEP | DEP |
Vamos chamar cada variável que será preenchida de célula, o nosso exemplo consiste em 3 departamentos (D1, D2, D3) e iremos preencher cada célula com estes departamentos. Cada coluna representa um turno.
Cada departamento deve ter uma quantidade de calouros que desejam em turnos, e a soma total de calouros pedidos deve ser igual ao total de calouros no evento, no caso 5 calouros.
Vamos supor que o D1 peça 2 calouros D2 peça 2 calouros e D3 peça 1 calouro por turno. Estes números podem variar a cada turno, mas no exemplo vamos supor que temos o mesmo número para todos os turnos.
Um exemplo de solução para o problema:
| t1 | t2 | t3 | t4 | |
| 1 | D1 | D2 | D1 | D2 |
| 2 | D2 | D1 | D3 | D2 |
| 3 | D2 | D3 | D2 | D1 |
| 4 | D3 | D1 | D2 | D1 |
| 5 | D1 | D2 | D1 | D3 |
Aqui vemos que não é possível evitar repetições para os departamentos D1 e D2, pois a quantidade de calouros pedidos por turno somados em todos os turnos é maior que a quantidade de calouros.
Para D1 e D2 temos:
2 + 2 + 2 + 2 = 8
Para D3 temos:
1 +1 + 1 + 1 = 4
Como temos apenas 5 calouros, podemos calcular quantas repetições irá acontecer no mínimo para cada departamento.
Para D1 e D2 teremos
8 - 5 = 3
Para D3 teremos
4 - 5 = -1
Ou seja, 3 calouros irão repetir os departamentos D1 e D2, e 1 calouro deixará de participar do departamento D3.
As repetições que entram neste cálculo são inevitáveis então se alcançarmos este mínimo de repetições dado por esta matemática chegaremos na escala ideal. O exemplo dado é uma escala ideal.
Conforme aumentamos a quantidade de departamentos e número de calouros, aumentamos a complexidade do problema.
Esta matemática é simples de ser observada no exemplo dado. Mas na escala real temos outros fatores que podem alterar este cálculo tornando-o mais difícil de ser respeitado como pedidos pessoais para um determinado departamento, departamentos que necessita de um determinado número de homens para os turnos ou mesmo escalas pré-definidas pelo próprio operador que alteram as possibilidades do problema.
Aí que entramos com programação por restrição, que deve respeitar algumas restrições de alta prioridade e de baixa prioridade.
Vamos separar as restrições em altas e baixas, sendo altas com prefixo R e baixas com prefixo B.
R1 - Calouros da área podem ser requisitados para o departamento específico.
R2 - Alguns departamentos pedem um número de homens mínimo dentre os calouros pedidos para um determinado turno.
R3 - O sistema deve manter escalas pré-definidas pelo operador.
R4 - O primeiro turno pode não ter atendimento em alguns departamentos por falta de população a ser atendida (geralmente apenas no primeiro turno) então estes departamentos poderão ser repetidos sem que isso seja considerado uma repetição.
B1 - Quando acontecer uma repetição é melhor que a repetição não seja consecutiva. De preferência o mais distante possível.
B2 - É bom empurrar as repetições para o fim do evento, pois os calouros podem fazer pedidos para passar em determinados departamentos mais para o final do evento, além de ocorrem muitas mudanças não previstas.
Agora como vamos respeitar e tratar cada uma das restrições? Teremos que integrar cada uma das restrições no algoritmo final.
R1 como o número de calouros de uma determinada área é muito pequeno e os pedidos para estes são geralmente em dias determinados, não vamos automatizar esta distribuição, vamos deixar que o usuário defina diretamente na escala, que dia o determinado calouro da área irá passar pelo departamento específico.
R2 terá de ser resolvido separadamente dos demais, pois se coloco mais homens do que o requisitado pelo departamento por dia será mais provável que haja repetições para o homem. Para diminuir esta possibilidade, os homens serão os primeiros a serem distribuídos dentre os departamentos que pediram homens.
R3 Escalas pré-inseridas pelo operador não poderão ser alteradas pelo sistema. Elas serão inseridas dentro da estrutura de dados como já preenchidas. O operador deve tomar cuidado para não exceder o número de calouros de um departamento para o mesmo dia, pois estes erros não serão corrigidos pelo sistema.
R4 será resolvido de forma que o usuário deve selecionar os departamentos que não tiveram turno e os calouros que foram para estes departamentos serão considerados que não passaram pelos mesmos, podendo assim repeti-los sem que seja considerada uma repetição.
B1 vamos respeitar esta restrição de baixa prioridade em departamentos que não foram recentemente passados pelo calouro.
B2 é fácil de respeitar, basta distribuir a partir do primeiro turno e resolver turno a turno, fazendo com que as repetições fiquem para os últimos turnos. Embora que, para chegarmos numa escala ideal, seja necessário colocar uma repetição no começo do evento, repetições voluntárias dos calouros irão minimizar este tipo de problema.
Vamos mostrar agora de uma forma bem didática, como funciona programação por Restrições com pontuação. Que foi o algoritmo implementado para resolver o sistema.
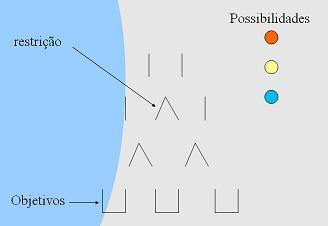
Na seguinte figura podemos mostrar como funcionam as restrições, imagine que temos 3 bolas de cores diferentes, o objetivo é preencher as 3 vasilhas ao fundo com uma bola cada, deixando o mínimo de vasilhas vazias respeitando restrições que cada bola pode ter.
Cada bola possui um conjunto de restrições mostradas nas próximas figuras.

Os números são as possibilidades de cada bola, bolas com mais restrições possuem menos possibilidades de preenchimento.
Começamos a preencher pelas bolas com menor quantidade de possibilidades. Quando preenchemos uma possibilidade, as possibilidades das demais bolas podem diminuir se elas estiverem no mesmo conjunto de possibilidades da bola que foi preenchida. Se ela não pertence a este conjunto, sua chance de ser preenchida não muda.
Selecionamos primeiro a bola que tem menor possibilidade que é a bola azul ou amarela com 2 possibilidades de preenchimento (ver figura anterior), no programa deixamos que as escolhas como estas sejam randômicas.
Selecionamos então a bola azul e a deixamos cair até uma das possibilidades, e a partir do momento que ela foi preenchida, devemos atualizar as possibilidades das demais bolas. No caso, a bola laranja cai de 3 possibilidades para 2 e a bola amarela para apenas 1 possibilidade como vemos na próxima figura.
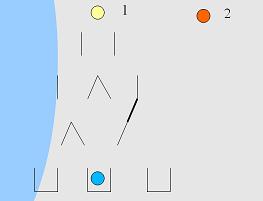
Agora escolhemos a bola amarela que possui apenas uma possibilidade de preenchimento. Aqui é fácil ver que se escolhêssemos a bola laranja poderíamos tirar a chance de a amarela ser preenchida.
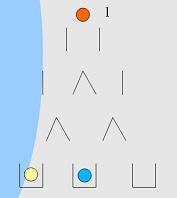
Agora basta colocar a ultima bola vermelha na sua única possibilidade de preenchimento, completando todas as possibilidades sem falta.
Não é tão claro como foi implementado este algoritmo dentro da varias restrições que existem dentro do programa, então vou explicar como foi implementado dentro do programa.
Há uma fila sem repetição para cada departamento com todos os calouros possíveis de serem preenchidos, se quisermos não deixar um calouro passar num determinado departamento, basta retirar ele desta fila.
Quando um calouro sai da fila sem repetição ele entra numa fila com repetição, e esta fila só é utilizada quando não há mais possibilidades livres na primeira fila.
Para selecionarmos os primeiros departamentos a serem preenchidos, selecionamos primeiro os departamentos com menor quantidade de possibilidades de preenchimento (menos calouros).
Primeiramente, escalamos os homens para que diminua a possibilidade de cair mais homens que o necessário para os departamentos que exijam homens, minimizando assim sua repetição.
Poderíamos utilizar backtraking para tentar melhorar a resposta do sistema quando a resposta não é a ideal dentro da programação por restrição.
Backtraking é refazer a escala tendo guardado em memória as escalas anteriores, procurando por escalas melhores que satisfazem o problema. Como a complexidade e processamento aumentam muito principalmente utilizando restrição com pontuação não implementamos isso. Se não utilizarmos pontuação, podemos fazer backtraking tentando jogar todas as bolas para um lado até achar uma solução e começamos voltar e tentar outras possibilidades recursivamente passando por todo o conjunto de soluções do problema sem muita dificuldade, mas exigiria muito mais processamento.
No lugar de backtraking implementamos um algoritmo TABU com um critério de parada bem curta de profundidade 2 de tentativas de troca.
Quando é encontrada uma repetição de departamento, o sistema procura um calouro na fila de departamentos não repetidos para trocar o departamento com o calouro que está repetindo, tentando eliminar esta falta.
Se ele não encontra, busca um terceiro calouro que possa trocar de departamento com o segundo e este novamente trocar com o que está com a repetição. Isto que significa a profundidade 2.
Não é utilizada uma profundidade maior por que as melhoras não são significativamente maiores e o tempo de processamento se torna exponencial mais longo.