As features implementadas foram:
- Raw
- LBP
- Moments
- Fourier
- Sobel
- HoG
Esta página contém uma breve descrição de cada feature. Maiores detalhes sobre cada uma delas podem ser encontrados na monografia.
As features implementadas foram:
Esta página contém uma breve descrição de cada feature. Maiores detalhes sobre cada uma delas podem ser encontrados na monografia.
A feature Raw é a feature mais simples que pode ser extraida de uma região de uma imagem. Dada uma determinada janela dentro de uma imagem, um vetor de características é criado com as intensidades de cada pixel daquela janela ao vetorizar a região.
Essa feature foi a primeira a ser implementada na TRIOSlib e foi a mais usada em outros papers
Essa feature foi baseada no descritor de textura Local Binary Pattern. Esse descritor se baseia na ideia de que texturas de duas dimensões podem ser representadas por duas medidas: padrão espacial local e contraste de níves de cinza. O Local Binary Pattern foi proposto por Ojala et. al. em 1994 [1]. Esse descritor se baseia no seguinte algoritmo:
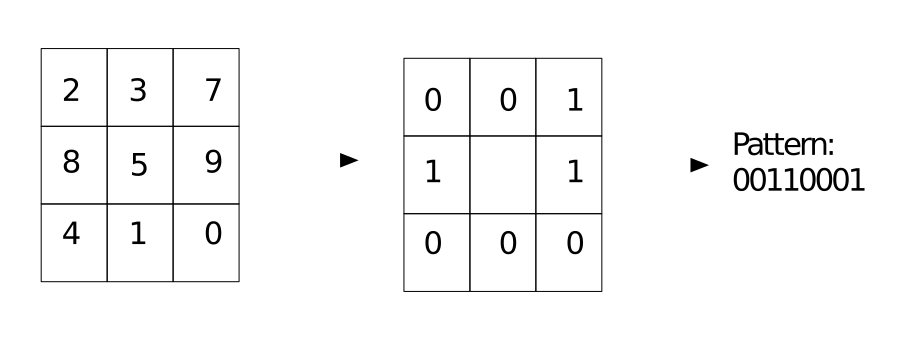 A nossa proposta é calcular a imagem formada pelo algoritmo do LBP aplicado na imagem original, e usar a janela correspondente na imagem do LBP
como feature para o algoritmo de aprendizagem.
A nossa proposta é calcular a imagem formada pelo algoritmo do LBP aplicado na imagem original, e usar a janela correspondente na imagem do LBP
como feature para o algoritmo de aprendizagem.
Seja f(x,y) a intensidade de nível de cinza da imagem f na posição (x,y). Se considerarmos f como sendo contínua, temos os momentos invariantes de uma
imagem definidos como:
Em 1962, Hu provou o teorema de unicidade dos momentos, mostrando que, se f(x,y) é contínua por partes e possui valores diferentes de zero apenas na parte finita do plano xy, existem momentos de todas as ordens e são unicamente determinados por f(x,y), e f(x,y) também é unicamente determinada pelos momentos.
Além do teorema de unicidade, os momentos invariantes podem ser usados para calcular propriedades da imagem como a área ou os centroides [2].
Podemos calcular, no plano discreto, uma estimativa dos momentos da seguinte forma:
Nossa proposta é de calcular os momentos geométricos de uma janela da imagem e usar esses momentos como vetor de características. O vetor de características é definido como: M = [f(x,y), x0, y0, m00, m01, m10, ..., mPQ] Onde x0 := m10/m00 e y0 := m01/m00 são os centróides.