É possível
determinar um intervalo de valores para os elementos da matriz 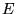 que compõe a matriz que compõe a matriz 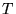 a partir das restrições físicas de valores existentes
para as matrizes a partir das restrições físicas de valores existentes
para as matrizes 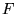 ou ou 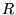 . Cada elemento da matriz . Cada elemento da matriz 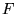 deve possuir valor entre 0 e 1 e cada elemento da matriz R deve possuir
valor entre 0 e 255. deve possuir valor entre 0 e 1 e cada elemento da matriz R deve possuir
valor entre 0 e 255.
Podemos calcular
a matriz 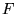 da seguinte maneira: da seguinte maneira:
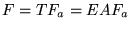 |
(16) |
Dessa maneira, podemos
representar cada elemento de 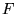 como sendo: como sendo:
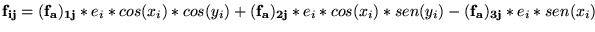
|
(17) |
onde
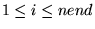 e e
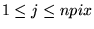 . .
Cada coluna de 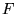 representa a proporção do componente puro em uma banda,
então cada elemento deve ter valor entre 1 e zero e a soma dos valores
da coluna deve ser igual a 1, então chegamos às seguintes restrições: representa a proporção do componente puro em uma banda,
então cada elemento deve ter valor entre 1 e zero e a soma dos valores
da coluna deve ser igual a 1, então chegamos às seguintes restrições:
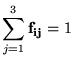 |
(18) |
onde
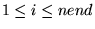 , e , e
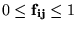 |
(19) |
onde
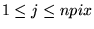 . .
Podemos usar qualquer algoritmo para resolver esse problema linear determinando
os valores máximos e mínimos para a matriz de transformação
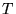 , através do qual determinamos os possíveis valores da matriz , através do qual determinamos os possíveis valores da matriz
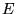 . .
Usando a função do MATLAB
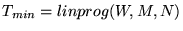 que resolve o problema linear que resolve o problema linear
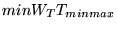 tal que tal que
 e e
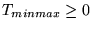 , onde , onde 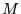 , , 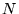 , , 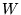 e e 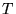 são matrizes, através da seguinte definição: são matrizes, através da seguinte definição:
![\begin{displaymath}
MT_{minmax} \leq N \longrightarrow \left[
\begin{array}{cc c...
...dots \\
1 \\
0 \\
0 \\
\vdots \\
0
\end{array}\right]\end{displaymath}](img52.png) |
(20) |
onde a matriz 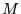 é uma composição da matriz é uma composição da matriz 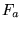 e e 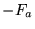 com tamanho 3 x 2n, onde com tamanho 3 x 2n, onde 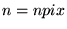 e a matriz e a matriz 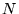 tem tamanho 1 x (npix+npix) e a matriz tem tamanho 1 x (npix+npix) e a matriz 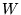 tem a seguinte definição: tem a seguinte definição:
![\begin{displaymath}
W = \left[
\begin{array}{cc cc}
1 & 0 & 0 \\
0 & 1 & 0 \\ ...
...& 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & -1 \\
\end{array}\right]\end{displaymath}](img55.png) |
(21) |
Dessa forma obtemos
os valores máximos e mínimos da matriz de transformação
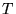 que correspondem aos valores da matriz que correspondem aos valores da matriz
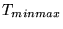 , onde cada linha possui valores de máximo e mínimo
relativos à cada coluna de valores da matriz , onde cada linha possui valores de máximo e mínimo
relativos à cada coluna de valores da matriz 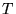 . O menor valor da linha de . O menor valor da linha de
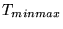 corresponde ao menor valor da coluna de corresponde ao menor valor da coluna de 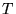 relativa e o valor máximo da linha relativa e o valor máximo da linha
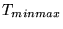 corresponde ao valor máximo valor da coluna de corresponde ao valor máximo valor da coluna de 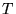 relativa. Então obtemos os seguintes vetores: relativa. Então obtemos os seguintes vetores:
![\begin{displaymath}
(T_{min})_{coluna} = \left[
\begin{array}{cc cc}
(t_{min})_{1} & (t_{min})_{2} & (t_{min})_{3} \\
\end{array}\right]\end{displaymath}](img57.png) |
(22) |
![\begin{displaymath}
(T_{max})_{coluna} = \left[
\begin{array}{cc cc}
(t_{max})_{1} & (t_{max})_{2} & (t_{max})_{3} \\
\end{array}\right]\end{displaymath}](img58.png) |
(23) |
Onde o vetor
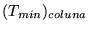 se refere aos valores mínimos de cada coluna
da matriz se refere aos valores mínimos de cada coluna
da matriz 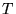 e e
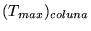 se refere aos valores máximos. se refere aos valores máximos.
Para calcular o valor
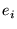 da matriz da matriz 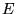 , primeiro determina-se seu intervalo de possíveis valores. Podemos
representar , primeiro determina-se seu intervalo de possíveis valores. Podemos
representar 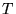 da seguinte maneira: da seguinte maneira:
![\begin{displaymath}
T = \left[
\begin{array}{cc cc}
e_{1}*cos(x_1)*cos(y_1) & e_...
...{3}*cos(x_3)*sen(y_3) & -e_{3}*sen(x_3) \\
\end{array}\right]\end{displaymath}](img62.png) |
(24) |
onde os ângulos
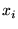 e e 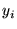 são determinados aleatoriamente. são determinados aleatoriamente.
Denominanos 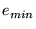 o vetor de valores mínimos para o vetor de valores mínimos para 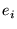 e e 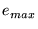 o vetor de valores máximos para o vetor de valores máximos para 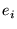 . Calculamos . Calculamos 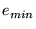 e e 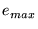 da seguinte maneira: da seguinte maneira:
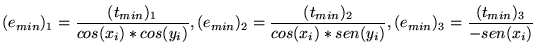
|
(25) |
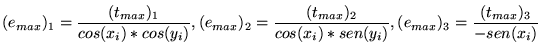
|
(26) |
Então, o intervalo
de possíveis valores para 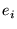 é é
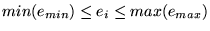 , onde , onde
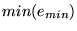 é o menor valor encontrado para no vetor é o menor valor encontrado para no vetor 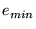 e e
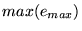 é o maior valor encontrado para o vetor é o maior valor encontrado para o vetor 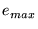 . .
Dentro desse intervalo
de valores, pode-se realizar uma busca para determinar um possível
valor de 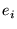 em um espaço de busca mais reduzido de forma a encontrar
mais facilmente um matriz em um espaço de busca mais reduzido de forma a encontrar
mais facilmente um matriz 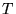 que satisfaça o problema. que satisfaça o problema. |