Classifica-se
a matriz 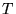 como uma matriz de transformação através da qual consegue-se
aproximar as matriz abstratas como uma matriz de transformação através da qual consegue-se
aproximar as matriz abstratas 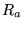 e e 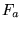 obtidas às matrizes desejadas obtidas às matrizes desejadas 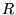 e e 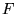 , logo, representa a solução do problema. , logo, representa a solução do problema.
Podemos representar a matriz 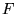 da seguinte maneira: da seguinte maneira:
![\begin{displaymath}
F = \left[
\begin{array}{cc cc}
\longleftarrow \mathbf{f_{1j...
...ftarrow \mathbf{f_{3j}} \longrightarrow \\
\end{array}\right]\end{displaymath}](img32.png) |
(11) |
onde
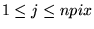 . A matriz . A matriz 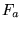 pode ser representada da mesma maneira. pode ser representada da mesma maneira.
A matriz 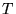 é uma transformação que leva cada ponto do espaço
de matrizes abstratas ao espaço de matrizes reais de maneira única,
então a matriz pode ser classificada como uma transformação
linear (Barone[1],Callioli[2]). é uma transformação que leva cada ponto do espaço
de matrizes abstratas ao espaço de matrizes reais de maneira única,
então a matriz pode ser classificada como uma transformação
linear (Barone[1],Callioli[2]).
Entretanto o espaço de busca da matriz 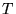 é muito grande, pois consiste em todo o espaço gerado por
quaisquer três vetores, tornando-se viável determinar somente
o subspaço que contém a matriz é muito grande, pois consiste em todo o espaço gerado por
quaisquer três vetores, tornando-se viável determinar somente
o subspaço que contém a matriz 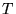 de resposta. de resposta.
A análise entre os vetores 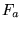 e e 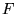 e e 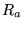 e e 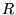 mostrou que a partir dos ângulos entre seus vetores é possível
obter a seguinte de decomposição de mostrou que a partir dos ângulos entre seus vetores é possível
obter a seguinte de decomposição de 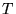 : :
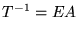 |
(12) |
onde 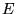 é uma matriz de escala da forma: é uma matriz de escala da forma:
![\begin{displaymath}
E = \left[
\begin{array}{cc cc}
e_{1} & 0 & 0\\
0 &e_{2} & 0\\
0 & 0 & e_{3}\\
\end{array}\right]\end{displaymath}](img36.png) |
(13) |
e a matriz 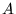 tem a seguinte forma: tem a seguinte forma:
![\begin{displaymath}
A = \left[
\begin{array}{cc cc}
cos(\mathbf{f_{1j}},\mathbf...
...(\mathbf{f_{3j}},\mathbf{(f_{a})_{3j}}) \\
\end{array}\right]\end{displaymath}](img38.png) |
(14) |
onde cada cosseno foi obtido do ângulo calculado entre os vetores
de 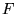 e e 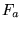 , onde , onde 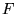 e e 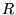 foram gerados aleatoriamente. A mesma analogia pode ser feita com
os ângulos das matrizes foram gerados aleatoriamente. A mesma analogia pode ser feita com
os ângulos das matrizes 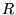 e e 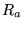 . .
A razão da existência da matriz 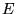 se deve ao fato de que o espaço representado pela matriz se deve ao fato de que o espaço representado pela matriz 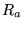 pode estar em uma escala diferente da original. Após análise
dos padrões formados pela matriz pode estar em uma escala diferente da original. Após análise
dos padrões formados pela matriz 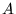 , reduziu-se a matriz , reduziu-se a matriz 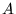 à seguinte matriz composta de coordenadas esféricas: à seguinte matriz composta de coordenadas esféricas:
![\begin{displaymath}
A = \left[
\begin{array}{cc cc}
cos(x_1)*cos(y_1) & cos(x_1...
...os(y_3) & cos(x_3)*sen(y_3) & -sen(x_3) \\
\end{array}\right]\end{displaymath}](img39.png) |
(15) |
Com a decomposição da matriz 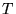 , determinou-se um subespaço dentro do espaço de possibilidades
que formam todas as possíveis composições de matrizes que
levam à matriz , determinou-se um subespaço dentro do espaço de possibilidades
que formam todas as possíveis composições de matrizes que
levam à matriz 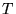 , de forma a reduzir o tempo de busca por uma matriz , de forma a reduzir o tempo de busca por uma matriz 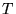 com tais configurações. com tais configurações. |