


MAC0499 - Trabalho de Formatura Supervisionado
Proposta para Monografia
Diferentes abordagens para problemas
de empacotamento
Aluno: Rafael Durbano Lobato
Orientador: Ernesto G. Birgin
Tipo de trabalho: Iniciação científica (com apoio financeiro
da FAPESP)
Resumo:
O problema clássico de empacotamento de retângulos em retângulos
consiste em arranjar ortogonalmente itens retangulares, de dimensões
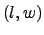 , num retângulo maior, de dimensões
, num retângulo maior, de dimensões  , sem
sobreposição. O objetivo é determinar uma disposição com a maior
quantidade possível de itens. Conjectura-se que a versão
não-guilhotinada do problema é
NP-difícil. Neste trabalho abordaremos este problema, assim como
uma variante na qual os itens retangulares devem ser empacotados em
regiões convexas arbitrárias. Para os dois problemas,
estudaremos os métodos existentes e proporemos novos modelos e
algoritmos.
, sem
sobreposição. O objetivo é determinar uma disposição com a maior
quantidade possível de itens. Conjectura-se que a versão
não-guilhotinada do problema é
NP-difícil. Neste trabalho abordaremos este problema, assim como
uma variante na qual os itens retangulares devem ser empacotados em
regiões convexas arbitrárias. Para os dois problemas,
estudaremos os métodos existentes e proporemos novos modelos e
algoritmos.
Palavras-chave: Empacotamento, modelos, programação
não-linear, programação dinâmica, algoritmos recursivos.
Neste trabalho abordaremos inicialmente duas variantes do problema de
empacotamento de retângulos: (a) empacotamento ortogonal de
retângulos em retângulos (problema de carregamento de palete - PCP)
e (b) empacotamento ``ortogonal'' de retângulos em regiões convexas
arbitrárias. O PCP consiste em arranjar, sem sobreposição, caixas
retangulares idênticas num palete retangular. As caixas devem ser
colocadas ortogonalmente, isto é, seus lados devem ser paralelos aos
lados do palete, e podem sofrer rotações de 90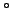 . O objetivo é
determinar um arranjo com a maior quantidade possível de caixas.
. O objetivo é
determinar um arranjo com a maior quantidade possível de caixas.
Morabito e Morales [11] apresentaram um método para
empacotar ortogonalmente retângulos idênticos 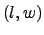 e
e 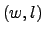 em um retângulo
em um retângulo  , sem sobreposição, considerando que
, sem sobreposição, considerando que
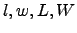 são inteiros positivos satisfazendo
são inteiros positivos satisfazendo 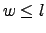 ,
, 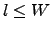 e
e 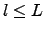 .
Trata-se de um procedimento recursivo, que divide o retângulo em cinco
partes (seguindo o padrão de corte não-guilhotinado de primeira ordem),
cada uma destas com tamanhos
.
Trata-se de um procedimento recursivo, que divide o retângulo em cinco
partes (seguindo o padrão de corte não-guilhotinado de primeira ordem),
cada uma destas com tamanhos
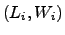 , conforme a Figura
1, e resolve o problema para cada uma destas novas partes.
, conforme a Figura
1, e resolve o problema para cada uma destas novas partes.
Figura 1:
Divisão do retângulo em cinco partes.
|
Os locais onde são feitas as divisões são determinados pelas
coordenadas 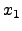 ,
, 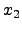 ,
, 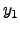 e
e 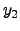 , como mostra a Figura
2. Como
, como mostra a Figura
2. Como 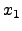 e
e 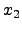 pertencem ao conjunto
pertencem ao conjunto
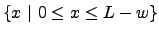 e
e 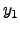 e
e 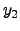 ao conjunto
ao conjunto
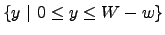 , existem infinitas possibilidades de particionamento do
palete. No entanto, pode-se mostrar que estes conjuntos podem ser
reduzidos, sem perda de generalidade, aos conjuntos normais
(Beasley [2])
, existem infinitas possibilidades de particionamento do
palete. No entanto, pode-se mostrar que estes conjuntos podem ser
reduzidos, sem perda de generalidade, aos conjuntos normais
(Beasley [2])
ou aos conjuntos dos raster points (Scheithauer e
Terno [12])
onde
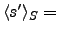 max
max
 . Esses conjuntos formam uma grade de pontos, limitando as
possibilidades de particionamento.
. Esses conjuntos formam uma grade de pontos, limitando as
possibilidades de particionamento.
Figura 2:
Pontos
 e
e
 que determinam a
divisão do retângulo.
que determinam a
divisão do retângulo.
|
Em outro trabalho, Lins, Lins e Morabito [8] propuseram
substituir o particionamento recursivo em cinco regiões por um
particionamento recursivo de um retângulo (R) ou uma peça em
forma de L (L) em duas peças, cada uma das quais sendo um
R ou um L. A eficiência do método depende
fortemente da quantidade de partições e do cálculo de
limitantes para o número de itens retangulares que podem ser
empacotados num determinado objeto.
A Figura 3 mostra um exemplo de
uma das possíveis divisões em L. Apesar dos autores afirmarem
que há sete formas de particionar um retângulo, aparentemente existem
mais duas, ilustradas na Figura 4, não relacionadas
neste artigo.
Figura 3:
Exemplo de divisão de um L em dois L's.
|
Em [8] os autores informam que foi possível resolver
todos os problemas de testes (mais de 20000, incluindo as 18 instâncias
não resolvidas pelo método anterior). Eles conjecturaram que a
abordagem em L sempre encontra empacotamentos ótimos de
retângulos 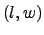 em peças retangulares.
em peças retangulares.
Figura 4:
Duas formas de particionar um retângulo em dois
L's, possivelmente não cobertas pelas divisões
relacionadas em [8].
|
Neste estudo queremos agregar ao método proposto em [8]
as vantagens da utilização dos conjuntos dos raster points
para formar a grade de particionamento. A cardinalidade destes
conjuntos é menor do que a dos conjuntos normais, podendo-se reduzir
consideravelmente a quantidade de chamadas recursivas ao método. Outro
ponto importante a ser abordado é o da determinação eficiente de bons
limitantes, principalmente inferiores, para o número de caixas que
podem ser arranjadas em um retângulo. Experimentos realizados
em [11] revelaram que o método pode se tornar muito mais
eficiente começando-se com um bom limitante inferior. É possível,
também, que uma combinação dos algoritmos propostos em [11]
e [8] resulte num programa com melhor desempenho,
utilizando-se os resultados do primeiro algoritmo como limitantes
inferiores iniciais para o segundo. Finalmente, analisaremos se a
inclusão dos novos padrões de cortes (apresentados neste projeto)
permite resolver o problema apresentado em [8] como
contra-exemplo de que o Algortimo-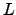 é ótimo para o problema de
empacotar retângulos num objeto com forma de
é ótimo para o problema de
empacotar retângulos num objeto com forma de 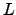 .
.
Modelos não-lineares têm sido recentemente empregados com sucesso
para modelar diversos problemas de corte e empacotamento. Uma
formulação não-linear para o problema bidimensional de cortes
não-guilhotinados foi apresentada em [4], onde o modelo
foi utilizado para a definição de uma heurística populacional. O
Método de Sentinelas para empacotamento de itens poligonais em objetos
arbitrários foi introduzida em [7]. O método é baseado em
análise convexa e formulações não-lineares para o tratamento da
sobreposição dos itens. Modelos não-lineares também foram utilizados
com sucesso em outros problemas de empacotamento, como o empacotamento
de moléculas [9] e o empacotamento de itens circulares em
diversos tipos de objetos [5,13,14,10], dentre
outros.
Em [6] é considerado o problema de empacotar, ortogonalmente,
itens retangulares em regiões convexas. O problema é modelado como o
problema de decidir se é possível empacotar 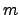 retângulos, com base
em um conjunto de equações e inequações não-lineares que compõem as
restrições do problema. Ao contrário deste, que possui restrições
sobre a orientação dos retângulos, o Método de Sentinelas [7]
permite rotações livres dos itens. A idéia principal está na definição
de um conjunto de pontos sobre cada item, com a propriedade de que
dois itens estão sobrepostos se, e somente se, pelo menos um destes
pontos de um item está no interior do outro. Tais pontos são chamados
de sentinelas e estão ilustrados na Figura 5.
retângulos, com base
em um conjunto de equações e inequações não-lineares que compõem as
restrições do problema. Ao contrário deste, que possui restrições
sobre a orientação dos retângulos, o Método de Sentinelas [7]
permite rotações livres dos itens. A idéia principal está na definição
de um conjunto de pontos sobre cada item, com a propriedade de que
dois itens estão sobrepostos se, e somente se, pelo menos um destes
pontos de um item está no interior do outro. Tais pontos são chamados
de sentinelas e estão ilustrados na Figura 5.
Figura 5:
Exemplo de um conjunto de sentinelas sobre um retângulo.
|
No caso do corte (ou empacotamento) possuir restrições de
ortogonalidade, os modelos são mais simples, no sentido de que os
problemas são mais fáceis de resolver, e são variantes do modelo
proposto em [6]. Esta situação pode ocorrer, por exemplo,
quando uma máquina não possui liberdade para efetuar cortes em
diversas direções, permitindo apenas cortes ortogonais, ou quando o
material a ser cortado é anisotrópico e deve-se manter uma determinada
orientação no desenho das peças. Por outro lado, se for interessante
permitir rotações livres dos itens a serem empacotados ou cortados,
então as restrições serão baseadas no conceito de sentinelas.
Com relação ao problema de carregamento de palete, pretendemos:
- (i)
- Considerar a possibilidade de utilizar a solução obtida pelo
método heurístico proposto em [11] como limitante
inferior inicial para o Algoritmo-
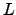 . Será importante avaliar se o
ganho obtido considerando este limitante compensará o custo de
calculá-lo.
. Será importante avaliar se o
ganho obtido considerando este limitante compensará o custo de
calculá-lo.
- (ii)
- Diminuir a quantidade de subproblemas que devem ser
resolvidos incorporando à implementação do método o conceito de
raster points [12].
- (iii)
- Pretendemos ainda, incorporar ao Algoritmo-
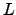 duas formas
de particionar um objeto em forma de
duas formas
de particionar um objeto em forma de 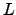 que não foram consideradas em
[8]. Analisaremos se, incorporando esses novos
particionamentos, é possível achar a solução ótima de um problema
específico de empacotar retângulos num objeto com forma de
que não foram consideradas em
[8]. Analisaremos se, incorporando esses novos
particionamentos, é possível achar a solução ótima de um problema
específico de empacotar retângulos num objeto com forma de 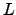 [8] que não é resolvido pela versão atual do método.
[8] que não é resolvido pela versão atual do método.
Com relação ao problema de empacotar itens retangulares numa
região convexa arbitrária, seguiremos de perto os métodos
propostos em [7,6]. Em [7] foi abordado o problema
de empacotar itens retangulares em regiões convexas arbitrárias
com rotações livres. Em [6] foi abordado o mesmo
problema, mas restringindo o empacotamento a configurações com
os itens ortogonais aos eixos cartesianos. No primeiro caso, a
liberdade das rotações livres tem o potencial de permitir que um
número maior de itens seja empacotado. Porém, o modelo que considera
as rotações livres, baseado no conceito de ``Sentinelas'', é um
modelo de programação não-linear mais difícil de ser resolvido
do que o modelo do problema que só permite rotações
ortogonais.
Pretendemos desenvolver um novo modelo que tente capturar as vantagens
dos dois modelos anteriores: (i) ter o potencial de empacotar um número
maior de itens; e (ii) ser fácil de resolver. Estamos nos referindo a
um modelo que modele a situação na qual os retângulos têm que
ser ortogonais entre si, mas não necessariamente ortogonais aos eixos
cartesianos. Esse modelo será adequado para o problema de corte no
qual a máquina de corte está restrita a fazer cortes ortogonais, mas
o objeto a ser cortado é isotrópico e, portanto, os itens não
precisam ter uma orientação fixa dentro do objeto.
Estudamos e implementamos o algoritmo descrito em [11],
incorporando de forma eficiente os conjuntos de raster points
[12]. Também estudamos e implementamos o algoritmo descrito em
[8]. Incorporamos os raster points ao
Algoritmo-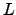 e introduzimos duas novas formas de dividir uma peça em
e introduzimos duas novas formas de dividir uma peça em
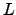 em dois novos
em dois novos 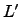 s, que não estavam previstas em
[8].
s, que não estavam previstas em
[8].
Provamos resultados importantes a respeito dos raster points.
Em particular, provamos resultados que mostram que: (i) as simetrias
envolvidas nas divisões dos retângulos continuam válidas com a
utilização de raster points e (ii) a quantidade de memória
exigida para armazenar informações dos subproblemas pode ser ainda
menor do que foi mostrado em [3].
- Julho: Realizar experimentos com problemas conhecidos na
literatura, apresentar resultados preliminares da implementação e
comparar o método modificado com a versão original.
- Agosto a novembro: Desenvolver o modelo de programação
não-linear que representa o caso de um único ângulo de
rotação para todos os itens. Tentar resolver o modelo com
algoritmos clássicos de programação não-linear (p.e.,
[1]).
- Novembro: Redação da parte subjetiva da monografia e
elaboração da apresentação e do pôster do trabalho.
A monografia será composta por duas partes: uma parte técnica, na qual
descreverei o trabalho realizado e uma parte subjetiva, onde será
relacionada a experiência adquirida na iniciação científica com o
Bacharelado em Ciência da Computação. A estrutura esperada da monografia
será a seguinte:
- Parte técnica
- Resumo;
- Introdução;
- Objetivos do trabalho;
- Algoritmo de cortes não-guilhotinados de primeira ordem;
- Algoritmo-
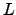 ;
;
- Modelos não-lineares;
- Conclusões;
- Bibliografia.
- Parte subjetiva
- Desafios e frustrações;
- Disciplinas cursadas no BCC mais relevantes para o trabalho;
- Interação com o orientador;
- Passos que tomaria se continuasse atuando na área;
- Conclusões.
- 1
-
R. Andreani, E. G. Birgin, J. M. Martínez e M. L. Schuverdt.
Augmented Lagrangian methods under the Constant Positive Linear
Dependence constraint qualification.
Mathematical Programming, 2005.
- 2
-
J. E. Beasley.
An exact two-dimensional non-guillotine cutting tree search
procedure.
Operations Research, 83:49-64, 1985.
- 3
-
E. G. Birgin, R. Morabito and F. H. Nishihara.
A note on an  -approach for solving the manufacturer's pallet
loading problem.
-approach for solving the manufacturer's pallet
loading problem.
Journal of the Operational Research Society, 56:1448-1451,
2005.
- 4
-
J. E. Beasley.
A population heuristic for constrained two-dimensional non-guillotine
cutting.
European Journal of Operation Research, 156:601-627, 2004.
- 5
-
E. G. Birgin, J. M. Martínez and D. P. Ronconi.
Optimizing the packing of cylinders into a rectangular container: A
nonlinear approach.
European Journal of Operational Research, 160:19-33, 2005.
- 6
-
E. G. Birgin, J. M. Martínez, F. H. Nishihara e D. P. Ronconi.
Orthogonal packing of rectangular items within arbitrary convex
regions by nonlinear optimization.
Computers & Operations Research, 33:3535-3548, 2006.
- 7
-
E. G. Birgin, J. M. Martínez, W. F. Mascarenhas e D. P. Ronconi.
Method of Sentinels for Packing Objects within Arbitrary Regions.
por aparecer em Journal of the Operational Research Society,
2005.
- 8
-
L. Lins, S. Lins e R. Morabito.
An  -approach for packing
-approach for packing  -rectangles into rectangular
and
-rectangles into rectangular
and  -shaped pieces.
-shaped pieces.
Journal of the Operational Research Society, 54(7):777-789,
2003.
- 9
-
J. M. Martínez e L. Martínez.
Packing optimization for automated generation of complex system's
initial configurations for molecular dynamics and docking.
Journal of Computational Chemistry, 24:819-825, 2003.
- 10
-
N. Mladenovic, F. Plastria e D. Uroševic.
Reformulation descent applied to circle packing problems.
Computers and Operations Research, 32(9):2419-2434, 2005.
- 11
-
R. Morabito e S. Morales.
A simple and effective recursive procedure for the manufacturer's
pallet loading problem.
Journal of the Operational Research Society, 49(8):819-828,
1998.
- 12
-
G. Scheithauer e J. Terno.
The G4-Heuristic for the Pallet Loading Problem.
Journal of the Operational Research Society, 47(4):511-522,
1996.
- 13
-
Y. G. Stoyan e G, Yaskov.
A mathematical model and solution method for the problem of packing
various-sized circles into a strip.
European Journal of Operational Research, 156:590-600, 2004.
- 14
-
H. Wang, W Huang, Q. Zhang e D. Xu.
An improved algorithm for the packing of unequal circles within a
larger containing circle.
European Journal of Operational Research, 141:440-453, 2002.
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html proposta.tex -style proposta.css -address http://www.ime.usp.br/ lobato/ -t 'Rafael Durbano Lobato' -split 1 -show_section_numbers -antialias
The translation was initiated by on 2006-07-03



http://www.ime.usp.br/~lobato/
![]() , num retângulo maior, de dimensões
, num retângulo maior, de dimensões ![]() , sem
sobreposição. O objetivo é determinar uma disposição com a maior
quantidade possível de itens. Conjectura-se que a versão
não-guilhotinada do problema é
NP-difícil. Neste trabalho abordaremos este problema, assim como
uma variante na qual os itens retangulares devem ser empacotados em
regiões convexas arbitrárias. Para os dois problemas,
estudaremos os métodos existentes e proporemos novos modelos e
algoritmos.
, sem
sobreposição. O objetivo é determinar uma disposição com a maior
quantidade possível de itens. Conjectura-se que a versão
não-guilhotinada do problema é
NP-difícil. Neste trabalho abordaremos este problema, assim como
uma variante na qual os itens retangulares devem ser empacotados em
regiões convexas arbitrárias. Para os dois problemas,
estudaremos os métodos existentes e proporemos novos modelos e
algoritmos.
![\includegraphics[width=137.3pt, height=135.4pt]{retangulo-5div.eps}](img12.png)
![\includegraphics[width=113.0pt, height=119.0pt]{retangulo-pontos-div.eps}](img30.png)
![\includegraphics[width=113.6pt, height=124.5pt]{divisao-L.eps}](img31.png)
![\includegraphics[width=311.8pt, height=125.3pt]{novasDivisoes.eps}](img32.png)
![\includegraphics[scale=0.45]{sentinelas.eps}](img35.png)