7. Ordenação

Problema geral: Dado um vetor com n >= 0 elementos, rearranje os elementos do vetor de forma que fiquem em ordem crescente: v[0] <= v[1] <= … <= v[n-1]

7.1. Ordenação por seleção

Ideia: Em cada passo encontra o maior do pedaço do vetor que estamos considerando e troca com o último. Em n-1 passos o vetor está ordenado.

44  75  12 27 *95* 15   3   73  19     maior: 95
44 *75* 12 27  19  15   3   73 [95]    maior: 75
44 *73* 12 27  19  15   3  [75  95]    maior: 73
...
Com n-1 passos, o vetor está ordenado
( )[                              ]

void troca(float v[], int i, int j) {
    float aux = v[i];
    v[i] = v[j];
    v[j] = aux;
}

void selecao(float v[], int n) {
    int i, imax, j;
    for (i = 1; i <= n-1; i++) {
        /* Invariante: Para todo i, sei que os i-1 maiores
         * números estão ordenados à direita.
         */
        imax = 0;
        for (j = 1; j <= n-i; j++) {
            /* Invariante: Para todo j, sei que imax contém o
             * índice do maior número até o j-ésimo elemento.
             */
            if (v[j] > v[imax])
                imax = j;
        }
        troca(v, n-i, imax);
    }
}

Anexo: selectionsort.c

Para analisar um loop em um algoritmo ou verificar sua corretude, utiliza-se técnicas como invariantes de loop: aquilo que está correto em todas as iterações.

7.1.1. Complexidade

Número de comparações:

\[n-1 + n-2 + ... + 1 = \dfrac{n(n-1)}{2}\]

Pior caso:

Comparações: \(O(n^2)\) Trocas: \(O(n^2)\).

Ideia: e se em cada iteração achássemos o máximo e o mínimo e trocássemos os dois?

 i-1            i-1
+------------------+
| <= |        | <= |
+------------------+

Temos \(n/2\) iterações.

Trocas: <=2 por iteração: \(O(n)\).

7.1.2. Recursivo

void selecaoRec(flat v[], int n) {
    int i, imax;
    if (n > 1) {
        imax = 0;
        for (i = 1; i < n; i++)
            if (v[i] > v[imax])
                imax = 1;
        troca(v, imax, n-1);
    }
    selecaoRec(v, n-1);
}

7.2. Bubble sort

Ideia: em cada iteração percorra o vetor comparando elementos vizinhos e trocando-os se estão na ordem errada. Quando não tiver mais elementos invertidos, o vetor estará ordenado. Sabemos que em cada iteração, um elemento vai pro lugar.

  44      44                 44  12                  12
- 75  12  12                 12  44  27              27
- 12  75  27                 27      44              44
- 27      75                 75          15          15
  95      95  15             15          75   3      3
  15      15  95  3           3              75  73  73
   3       3     93  73  73  73                  75  19
  73      73         95  19  19                      75
  19      19                 95                      95

void bubblesort(int v[], int n) {
    int i, j, trocou;

    for (i = 1; i < n; i++) {
        trocou = 0;
        for (j = 0; j < n-i; j++) {
            if (v[j+1] < v[j]) {
                troca(v, j, j+1);
                trocou = 1;
            }
        }

        if (!trocou) break;
    }
}

Anexo: bubblesort.c

7.2.1. Complexidade

Caso	Comparações	Trocas
Melhor (vetor ordenado)	\(O(n)\)	\(0\)
Pior (ordem inversa)	\(\dfrac{n(n-1)}{2} \implies O(n^2)\)	\(O(n^2)\)

7.2.2. Recursivo

void bubbleRec(float v[], int n) {
    int i, troca = 0;
    if (n > 1) {
        for (i = 0; i < n-1; i++) {
            if (v[i+1] < v[i]) {
                troca(v, i, i+1);
                trocou = 1;
            }
        }
        if (trocou)
            bubbleRec(v, n-1);
    }
}

7.3. Insertion sort

John Mauchly, 1946

Ideia: Em cada iteração o vetor está divido em duas partes: uma parte ordenada no início do vetor e uma parte bagunçada no resto. Pegamos o primeiro elemento da parte bagunçada e o inserimos na posição correta da parte ordenada.

ordenado            bagunça
[44]  75  12  27  95  15   3   73  19
[44   75] 12  27  95  15   3   73  19
[12   44  75] 27  95  15   3   73  19

// versão iterativa
void insercao(float v[], int n) {
    int b, i;
    float x;
    for (b = 1; b < n; b++) {
        x = v[b];
        for (i = b - 1; i >= 0 && v[i] > x; i--)
            v[i + 1] = v[i];
        v[i + 1] = x;
    }
}

// versão recursiva
void insercaoRec(float v[], int n) {
    int i; float x;

    if (n > 1) {
        insercaoRec(v, n-1);
        x = v[n-1];
        for (i = n-2; i>= 0 && v[i] > x; i--)
            v[i+1] = v[i];
        v[i+1] = x;
    }
}

7.3.1. Complexidade

• Melhor caso (lista ordenada):

  • Comparações: \(n-1 \implies O(n)\)
  • Movimentos: \(2(n-1)\)

• Pior caso (ordem inversa):

  • Comparações: \(1 + 2 + \ldots + n-1 = \dfrac{n(n-1)}{2} \implies O(n^2)\)
  • Movimentos: \(2(n-1)+\dfrac{n(n-1)}{2}\)

Uma análise de caso médio pode ser feita, assumindo por exemplo que para todo \(b=1, ..., n-1\) a probabilidade de \(x\) ser inserido em qualquer posição é \(1/b\).

\[\begin{split}\begin{align} \mathbb{E}(\text{no. de comparações}) &= 1 \cdot 1 + (1 + 2) 1/2 + (1 + 2 + 3) 1/3 + \ldots \\ &= \sum^n_{i+1}\left(1 + 2 + \ldots + i\right) \cdot 1/i \\ &= \sum^n_{i+1}\left(\dfrac{i(i+1)}{2}\right)\cdot \dfrac{1}{i} \\ \implies O(n^2) \end{align}\end{split}\]

7.3.2. Inserção binária

John Mauchly, 1946

Podemos melhorar o algoritmo com relação ao número de comparações.

 ordenado
[        ][              ]
 ^ busca binária

• Número de comparações:

\[\begin{split}\sum^{n}_{b=1}{log_2{b}} &\leq \int^n_1{\log_2{x} dx} \\ \int^n_1{log_2{x} dx} &= \dfrac{1}{\ln{2}} \int^n_1{ln{x} dx} \\ &= \dfrac{1}{\ln{2}}[x \ln{x}+x]^n_1 \\ &= \dfrac{1}{\ln{2}}(n \ln{n} + n - 1) &= n \log_2{n} + n -1 \\ \implies O(n \log_2{n})&\end{split}\]

7.4. Mergesort

von Neumann, 1945

Ideia: Divisão e conquista. O vetor é divido na metade e cada metade é ordenada. Então, os elementos são intercalados para obter o vetor ordenado.

[          |           ]

[ ordenado ][ ordenado ]

        intercala
[                      ]

117   195   81   43 | 15   79   18   80   47

43    81   117  195 | 15   18   47   79   80

15    18    43   47 | 79   80   81   117  195

void intercala(float v[], int p, int q, int r) {
    float *aux = maloc((r-p) * sizeof(float));
    int i = p, j = q, k =0;
    while (i < q && j < r)
        if (v[i] < v[j]) {
            aux[k] = v[i];
            k++; i++;
        }
        else {
            aux[k] = v[j];
            k++; j++;
        }

    while (i < q) {
        aux = v[i];
        k++; i++
    }

    while (j < r) {
        aux[k] = v[j];
        k++; j++;
    }

    for (i = p, k = 0; i < r; i++, k++)
        v[i] = aux[k];

    free(aux);
}

void mergesort(float v[], int ini, int fim) {
    int meio = (ini + fim)/2;
    if (fim > ini) {
        mergesort(v, ini, meio);
        mergesort(v, meio, fim);
        intercala(ini, meio, fim);
    }
}

Simulação:

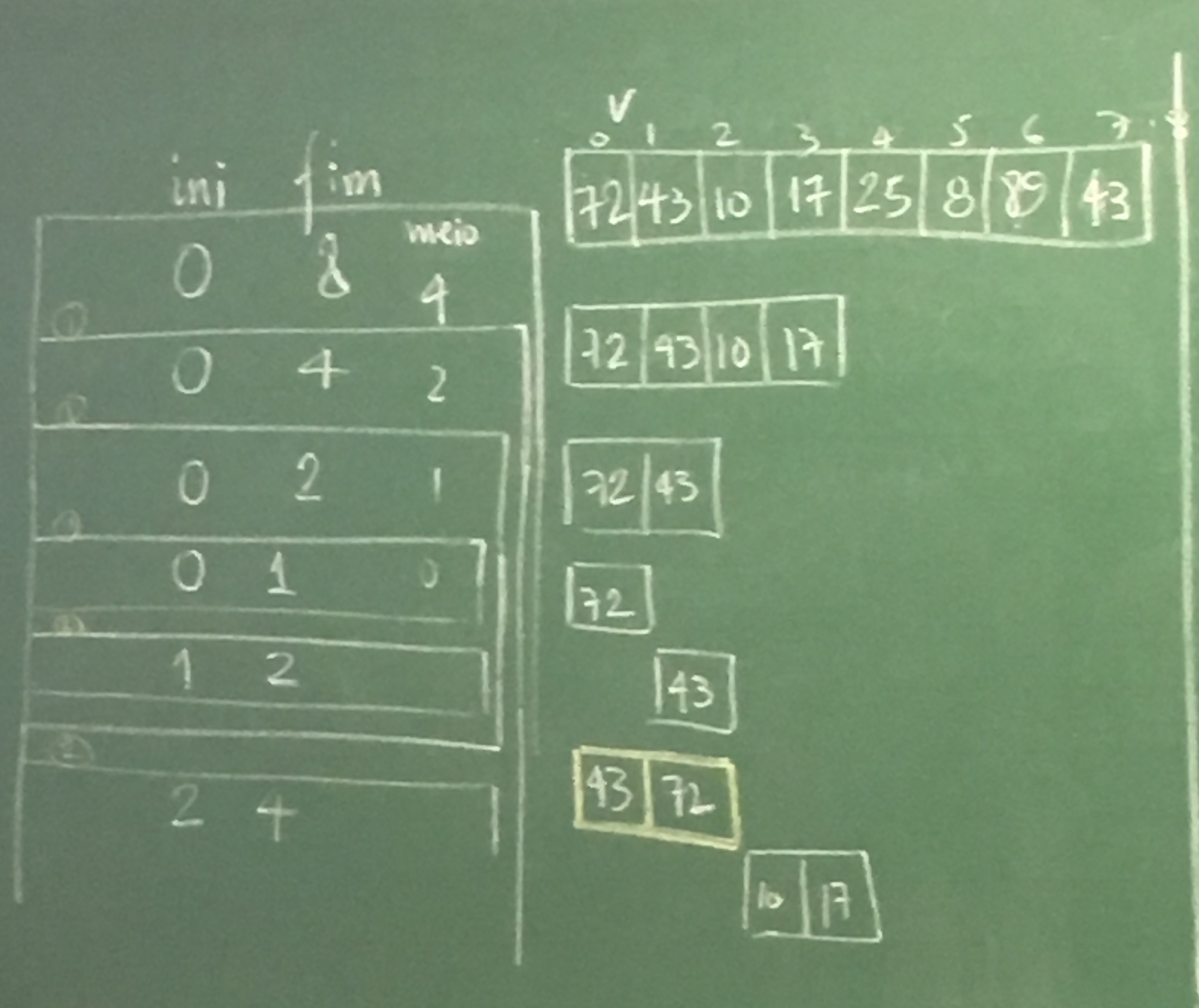
7.4.1. Complexidade

• Função intercala:

  • Número de comparações \(n-1 \implies O(n)\), onde \(n=r-p\).

O intercala tem complexidade linear. Assim, em cada nível, o mergesort divide o valor e ao chamar o intercala, o número total de comparações por nível é \(O(n)\).

A desvantagem do algoritmo é usar espaço extra para ordenar o vetor. É possível implementar o intercala sem usar espaço extra, perdendo na complexidade. É possível também implementar o mergesort em espaço adicional com a mesma complexidade.

7.5. Quicksort

Hoare, 1960

A ideia do algoritmo é aplicar divisão e conquista de uma forma diferente. Escolhemos um pivô e dividimos os elementos do vetor de forma que os menores ou iguais ao pivô são movidos para o início e os maiores para o fim.

[40] 12  25  45  72  10  39  14  23  42  37  61
 12  25  10  39  14  23  37 [40] 45  72  42  61
 |------------v------------|    |------v------|
 10 [12] 25  39  14  23  37      42 [45] 72  61
         14  23 [25] 39  37              61 [72]
        [14] 23      37 [39]

Com isso, o pivô vai para a posição correta no vetor ordenado.

      pivô
[  <=  []   >    ]

Basta, então, ordenar recursivamente os dois pedaços do vetor.

Se eu der sorte na escolha do pivô, cada execução do separa divide o vetor em dois pedaços de tamanho iguais.

[      []      ] n
[ []  ]  [ []  ] n/2
[ ] [ ]  [ ] [ ] n/4   logn

Se eu der azar,

n   [               []]
n-1 [[]               ]    |
n-2    [[]            ]    |  n-1
         [          []]    v

int separa(float v[], int ini, int fim) {
    int p = ini, q = fim - 1;
    float pivo = v[ini];
    while (p < q) {
        while (v[q] > pivo)
            q--;
        if (q > p)
            troca(v, p, q);
        while (p < q && v[p] <= pivo)
            p++;
        if (p < q)
            troca(v, p, q);
    }
    return p;
}

void Quicksort(float v[], int ini, int fim) {
    int pivo;
    if (fim - ini >= 2) {
        pivo = separa(v, ini, fim);
        Quicksort(v, ini, pivo);
        Quicksort(v, pivo+1, fim);
    }
}

Anexo: quicksort.c

7.5.1. Complexidade

Com isso, no melhor caso:

  n/2     n/2
[      []      ]     n    | log_2 n
[      ][      ]   < n    v
O(n log_2 n)

E no pior caso:

[           []]  n
[             ]  n-1       O(n^2)

7.5.2. Variação do Sedgewick

int separa(float v[], int ini, int fim) {
    /* R. Sedgewick */
    int i = ini - 1, j;
    float pivo = v[fim - 1];
    for (j = ini; j < fim; j++)
        if (v[j] <= pivo) {
            i++;
            troca(v, i, j);
        }
    return i;
}

7.5.2.1. Análise do caso médio

Seja \(C(n)\) o número total de comparações (*) executadas para ordenar um vetor com n elementos na média, considerando que a probabilidade do separa devolve qualquer índice é a mesma.

\[ \begin{align}\begin{aligned}\begin{split}C(n) = \begin{cases} 0 &\text{, se } n =1 \text{ ou } n = 1 \\ n + prob(\text{separa devolver o 1º})\cdot(C(0) + C(n-1)) + &\text{, se } n \geq 2 \\ prob(\text{separa devolver o 2º})\cdot(C(1) + C(n-2)) + \\ prob(\text{separa devolver o 3º})\cdot(C(2) + C(n-3)) + \\ \ldots \\ prob(\text{separa devolver último})\cdot(C(n-1) + C(0)) \\ \end{cases}\end{split}\\\begin{split}C(n) = \dfrac{1}{n}\left[C(0) + C(n-1) + C(1) + C(n-2) + \ldots + C(n-1) + C(0)\right] \\ C(n) = n + \dfrac{2}{n} \\ \sum^{n-1}_{i=0} c(i)\end{split}\end{aligned}\end{align} \]

7.5.3. Aleatorizado

Em cada chamada do algoritmo, um elemento do vetor é escolhido para pivô e o vetor é reorganizado:

[ <= x  (x)   > x     ]
         ^ pivô

Como fazer esta separação: 1. Hoare «closing gap»

v pivô
x   [  <=x  |        |  >x ]

2. Sedgewick

v pivo      i          j
x   [ <=x    |  >x    |    ]

int separaAleatorio(float v[], int ini, int fim) {
    int r = random(ini, fim);  // sorteia índice [ini, fim-1]
    troca(v, r, fim - 1);
    return separaSedgewick(v, ini, fim);
}

void quickSortAleatorizado(float v[], int ini, int fim) {
    int pivo;
    if (fim - ini > 1) {
        pivo = separaAleatorizado(v, ini, fim);
        quickSortAleatorizado(v, ini, pivo);
        quickSortAleatorizado(v, pivo + 1, fim);
    }
}

A versão aleatorizada do quicksort tem complexidade esperada \(O(n\log{n})\). Note que a probabilidade de ocorrer o pior caso é praticamente nula \(\dfrac{2^n}{n!}\).

7.5.3.1. Complexidade

• Melhor caso: \(O(n\log{n})\)
• Pior caso: \(O(n^2)\)
• Caso médio: \(O(n\log{n})\)

7.6. Heapsort

Williams, Floyd 1960

Uma heap é estrutura hierárquica (árvore) com as seguintes propriedades:

1. É completa até o penúltimo nível;
2. Os elementos do último nível estão o mais à esquerda possível;
3. Cada elemento é maior que seus filhos.

Exemplo:

         ___1__
        /      \
    ___21       17
   /     \     /  \
  20      1   8    14
 /  \
7    4

Um jeito simples de representar um heap é usando um vetor:

 0  1  2  3  4  5  6  7  8
[43|21|17|20| 1| 8|14| 7| 4]

Os filhos do elemento na posição \(i\) em \(2i+1\) e \(2i+2\). O pai do elemento na posição \(i\) está com \((i-1)/2\).

Suponha que temos uma função que recebe um vetor e o transforma num heap.

void rebaixa(float v[], int n, int i) {
    int pai, filho;
    pai = i; filho = 2*i + 1;

    while (filho < n) {
        if (filho + 1 < n && v[filho + 1] > v[filho])
            filho++;

        if (v[filho] < v[pai])
            break;
        else {
            troca(v, pai, filho)
            pai = filho;
            filho = 2*pai + 1;
        }
    }
}

void heapifica(float v[], int n) {
    int i;
    for(i = (n-2)/2; i >= 0; i--) {
        rebaixa(v, n, i);
    }
    // Numa primeira análise executamos n/2 * rebaixa, portanto,
    // O(nlogn).
    // Uma análise mais cuidadosa mostra O(n).
}

void heapifica(v, n) {
    heapifica(v, n);
    for (i = n-1; i > 0; i--) {
        troca(v, 0, i);
        heapifica(v, i);
        rebaixa(v, i, 0);
    }
}

30  27  10  17  19  48  39  4   25
48  39  30  25  10  27  19  17  4
4   39  30  25  10  27  19  17  48

        ____4___
       /        \
     _39        _30
    /   \      /   \
  _25    10   27    19
 /
17

7.7. Comparação

Algoritmo	Complexidade (pior caso)
Seleção	\(O(n^2)\) comparações, O(n) trocas
Bubblesort	\(O(n^2)\) comparações e trocas
Inserção	\(O(n^2)\) comparações e movimentos
Inserção binária	\(O(n \log_2{n})\) comparações \(O(n^2)\) movimentos
Mergesort	\(O(n \log_2{n})\)
Quicksort	\(O(n \log_2{n})\)

7.8. Links

• Sorting algorithms
• Gifs de ordenação

Terça-feira, 18 de setembro Quarta-feira, 20 de setembro