10. Árvores¶
Árvores são estruturas hierárquicas em que cada elemento (nó) está ligado a um número finito de sub-árvores disjuntas.
Exemplo 1
Os nós sem filhos são chamados de folhas da árvore. Todos os nós na árvore enraizada em um elemento são chamados de descendentes. No exemplo, os descendentes de G são G, K, N, O e P; as folhas estão sublinhadas.
Os elementos diretamente ligados a um nó são seus filhos. Todo nó, com exceção à raiz da árvore, tem um único pai.
Não é árvore pois um nó tem dois descendentes
Os ancestrais de um nó são os nós no caminho até a raiz. Ex: ancestrais de D são: D, B e A.
O grau de um nó é o número de filhos. Dizemos que uma árvore é \(k\text{-ária}\) se todos os nós tem grau menor ou igual a \(k\). A profundidade de um nó é o número de ancestrais próprios que ele tem.
A altura de uma árvore é dada pela profundidade máxima de uma de suas folhas. No exemplo 1, a altura da árvore é 4.
A árvore vazia tem altura -1. A árvore com apenas um nó tem altura zero.
Uma árvore é ordenada se faz diferença a ordem do filho. Por exemplo, as árvores a seguir são diferentes:
10.1. Representação¶
Como representar uma árvore \(k\text{-ária}\)?
10.1.2. Ponteiro¶
Primeira ideia
Representação de uma árvore k-ária, k=3
typedef struct no {
TipoDaArvore info;
struct no *pai;
struc no *filho[k];
} No;
Problema: gasto de espaço.
Segunda ideia
Representação eficiente de uma árvore usando ponteiros
typedef struct cel {
TipoDaArvore info;
struct cel *pai;
struct cel *filho;
struct cel *irmao;
} celula;
typedef celula *apontador;
int prof(apontador x) {
/* x != NULL */
int p = 0;
while (x->pai != NULL) {
p++;
x = x->pai;
}
return p;
}
int graumax(apontador t) {
// complexidade: O(n)
int graut, g, maxg;
apontador p;
graut = maxg = 0;
p = t->filho;
while (p != NULL) {
graut++;
g = graumax(p);
if (g > maxg) maxg = g;
p = p->irmao;
}
if (graut > maxg)
maxg = graut;
return maxg;
}
10.2. Árvores binárias¶
Árvores binárias são árvores ordenadas de grau máximo 2.
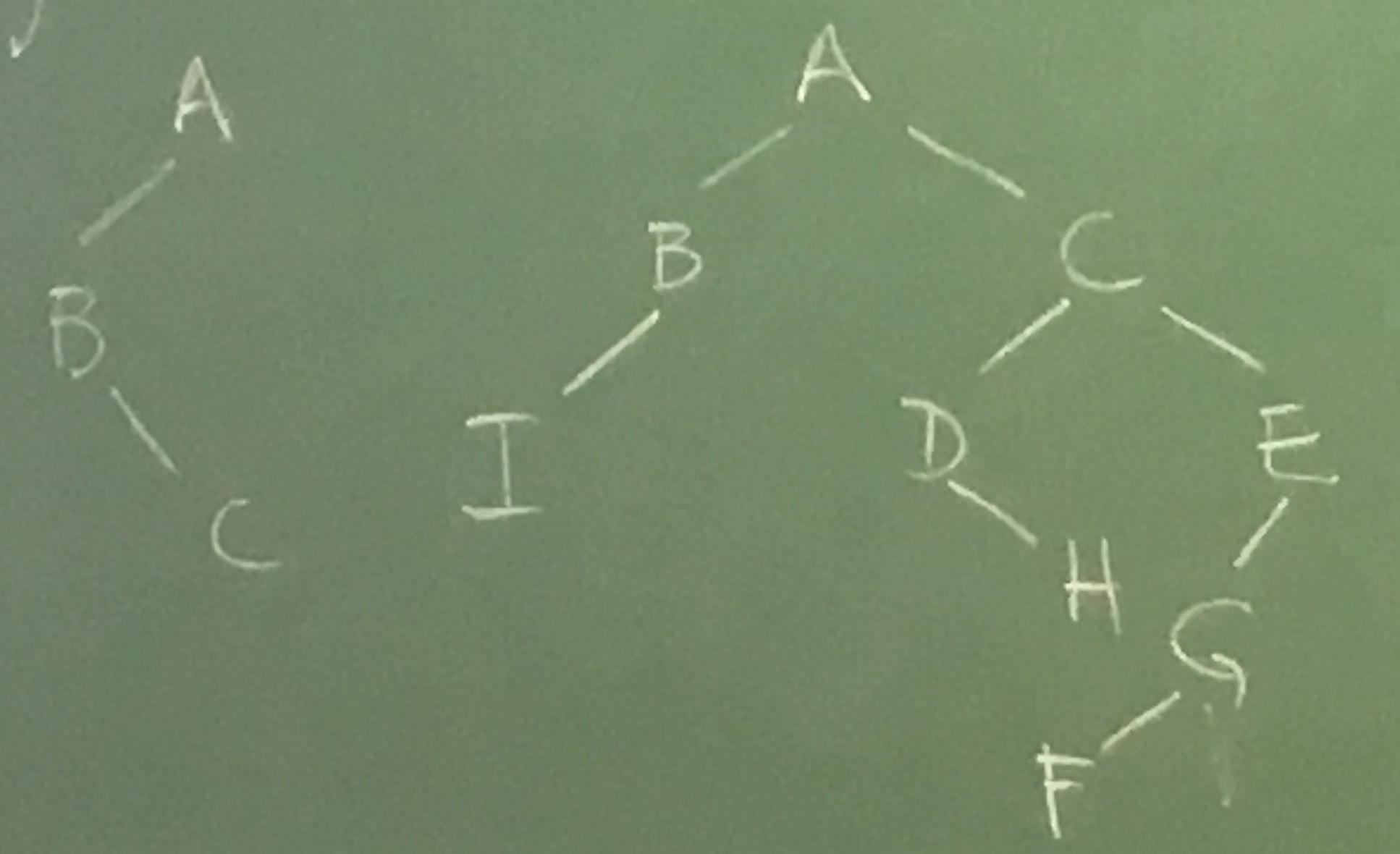
Quantas árvores binárias existem com n vértices?
| Vértices | Árvores |
|---|---|
| 1 | 0 |
| 2 | 2 |
| 3 | 5 |
| 4 | 14 |
| 5 | ? |
O número é dado por:
| Vértices | Árvores |
|---|---|
| 5 | 42 |
| 6 | 132 |
| 7 | 429 |
| 8 | 1430 |
| 9 | 4862 |
| 10 | 16796 |
Número de Catalan (séc XIX)
Uma árvore binária é completa se tem todas as folhas possíveis na sua profundidade máxima.

Uma árvore completa de altura h tem \(2^{h+1}-1\) nós e \(2^h\) filhos.

Uma árvore binária com n vértices tem altura:
Faça uma função que retorna a quantidade de vértices da árvore.
typedef struct no {
TipoDaArvore info;
struct no *pai;
struct no *esq;
struct no *dir;
} No;
typedef No *apontador;
int contaNos(apontador t) {
if (t->NULL) return 0;
return contaNos(t->esq) + contaNos(t->dir) + 1;
}
Faça uma função que calcula a altura da árvore.
int altura(apontador t) {
int d, e;
if (t == NULL) return -1;
e = altura(t->esq);
d = altura(t->dir);
if (d > e)
return d + 1;
else
return e + 1;
}
10.3. Percursos¶
10.3.1. Busca em profundidade¶
A B F G K L O D C H P J N Q R
10.3.2. Busca em largura¶
A B D F C J G H N K L P Q R O
10.3.3. Pré-ordem¶
A B F G K L O D C H P J N Q R (idêntico a busca em profundidade)
- r - Visita a raiz;
- E - visito a subárvore esquerda da raiz em pré-ordem;
- D - visito a subárvore direita da raiz em pré-ordem;
10.3.4. In-ordem¶
F K G O L B A H P C D J Q N R
- E - visita os nós da subárvore esquerda em in-ordem
- r - visita a raiz
- D - visita os nós da subárvore direita em in-ordem
10.3.5. Pós-ordem¶
K O L G F B P H C Q R N J D A
- E - visita os nós da subárvore esquerda em in-ordem
- D - visita os nós da subárvore direita em in-ordem
- r - visita a raiz
10.3.6. Aplicações¶
10.3.6.1. Notação Aritmética¶
Os nomes pré-ordem, in-ordem e pós-ordem são devidos a aplicação direta em converter as notações aritmética infixa, prefixa e pós-fixa.
É possível remontar a árvore usando a pré-ordem e in-ordem.
É possível remontar usando a pós-ordem a in-ordem.
Não é possível remontar usando pré-ordem e pós-ordem.
10.3.6.2. Exercícios¶
// menos eficiente (pode percorrer todos os vertices)
int ancestral(apostador p, apontador q) {
if (p == NULL || q == NULL)
return 0;
if (p == q)
return 1;
return ancestral(p->esq, q) || ancestral(p->direita, q);
// feio
// return p != NULL && q != NULL && p != q &&
// (ancestral(p->esq, q) || ancestral(p->direita, q));
}
// bem eficiente (percorre a distancia de vertices)
int ancestral(apostador p, apontador q) {
apontador aux = q;
if (p == NULL)
return 0;
while (aux != NULL && aux != p)
aux = aux->pai;
return aux == p;
}
int nivel(apontador p) {
/* p != NULL */
int cont = 0;
while (p->pai != NULL) {
cont++;
p = p->pai;
}
return cont;
}
apontador ancestralComumMaisProx(apontador p, apontador q) {
int np = nivel(p), nq = nivel(q);
while (np > nq) {
p = p->pai;
np--;
}
while (nq > np) {
q = q->pai;
nq--;
}
while (p != q) {
p = p->pai;
q = q->pai;
}
return p;
}
apontador ancestralComumMaisProx(apontador p, apontador q) {
while (ancestral(p, q) == 0)
p = p->pai;
return p;
}
void imprimeFolhas(apontador raiz) {
if (raiz != NULL) {
if (raiz->esq == NULL || raiz->dir == NULL)
printf("%c\n", raiz->info);
else {
imprimeFolhas(raiz->esq);
imprimeFolhas(raiz->dir);
}
}
}
10.4. Árvores de busca binária¶
Uma árvore de busca binária (ABB) é uma árvore binária em que:
- para cada nó, a informação de todo nó na subárvore esquerda é menor que a informação do nó
- todo nó da subárvore direita é maior.
Uma ABB armazena um conjunto.
__________43__________
/ \
____37___ _____74___
/ \ / \
17 _40 _53_ _84_______
/ \ / / \ / \
5 32 38 48 59 75_ _110
\ /
77_ 94
\
81
in-ordem: 5 17 32 37 38 40 ...
Fazer busca, mínimo, insere, remove.
Anexo: arvore-bb.c