11. Hashing¶
Uma tabela de símbolos é uma estrutura que implementa as operações de inserção e busca.
| Implementação | Busca | Inserção |
|---|---|---|
| Vetor | O(n) | O(1) |
| Vetor ordenado | O(log(n)) | O(n) |
| L.l. | O(n) | O(1) |
| L.l. ord | O(n) | O(1) |
| ABB | O(altura) | O(altura) |
| Hashing | O(1) | O(1) |
Uma tabela de hashing (espalhamento) é uma tabela em que os elementos que serão armazenados serão divididos.
Exemplo: Uma tabela com alunos da USP.
Ideia: Podemos usar o NUSP como índice de uma tabela:
Problema: Gasta muito espaço
2ª ideia: NUSP % 100
Problema: dois ou mais alunos podem ter o mesmo final de NUSP (colisão).
Para resolver a colisão poderíamos usar:
Mas como projetar uma boa função de hash?
Ideia: métodos da divisão
h(x) = x % m M é primo, próximo a n
É fácil para o «adversário» gerar um conjunto de dados ruim para a função.
Ideia (Knuth): multiplicação
Onde Frac é a parte fracionária.
Funções de hashing que garantem um bom espalhamento (a probabilidade de colisão é pequena) são difíceis de obter. Uma forma de obter isso é o chamado hashing universal (mais disso em MAC338).
12. Aplicações¶
12.1. Bucketsort¶
Suponha que queremos ordenar n números reais no intervalo \([0, 1)\).
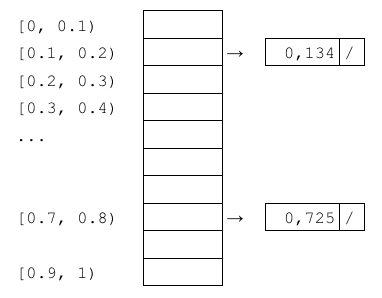
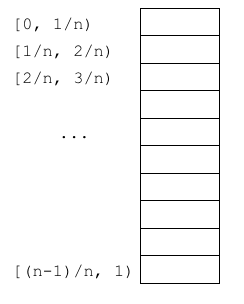
Este método pode ser usado para ordenar em tempo linear números desde que saibamos que eles estão num dado intervalo \(n, [a, b)\):
12.2. Radixsort¶
Cada passada tem complexidade \(\Theta(n)\), portanto em tempo \(\Theta(d \cdot n)\) o vetor é ordenado onde \(d\) é o número máximo de dígitos dos número que queremos adicionar.