34 Minimização Unidimensional

Esse capítulo descreve rotinas para procurar mínimos de funções arbitrárias unidimensionais. A biblioteca fornece componentes de baixo nível para uma variedade de minimizadores iterativos e testes de convergência. Esses minimizadores e testes podem ser combinados pelo usuário para encontrar a solução desejada, com acesso total aos passos intermediários dos algoritmos. Cada classe de métodos usa a mesma estrutura, de forma que você pode alternar entre minimizadores durante a execução sem precisar recompilar seu programa. Cada instância de um minimizador mantém registros de seu próprio estado, permitindo aos minimizadores serem usados em programas com suporte a multiplas linhas de execução.

O arquivo de cabeçalho ‘gsl_min.h’ contém protótipos para as funções de minimização e declarações relacionadas. Para usar os algoritmos de minimização para encontrar o máximo de uma função simplesmente inverta seu sinal.

34.1 Visão Geral

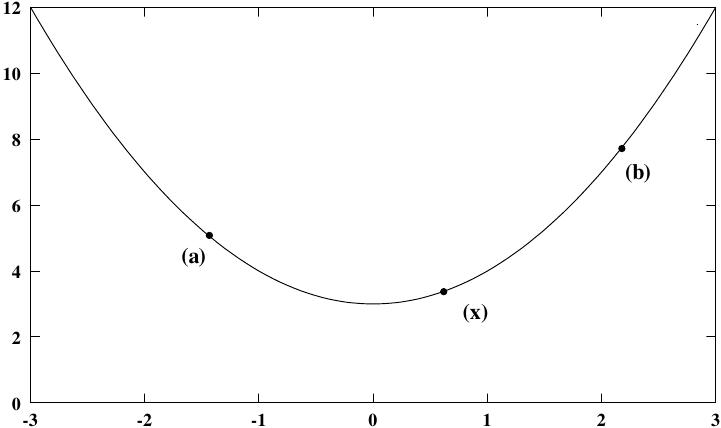
Os algoritmos de minimização iniciam com uma região limitada onde sabe-se estár contido um mínimo. A região é descritia por um limite inferior a e um limite superior b, com uma estimativa de localização do mínimo x.

O valor da função em x deve ser menor que o valor da função nas extremidades do intervalo,

Muitos algoritmos de delimitação estão disponíveis dentro de uma estrutura simples. O usuário fornece um norteador de alto nível para o algoritmo, e a bilioteca fornece as funções individuais necessárias para cada um dos passos. Existem três principais fases da iteração. Os passos são,

• inicialize o estado do minimizador, s, para o algoritmo T
• atualiza s usando a iteração T
• testa s com relação à convergência, e repete a iteração se necessário

O estado para os minimizadores é mantido em uma estrutura gsl_min_fminimizer. O procedimento de atualização usa somente avaliações de função (não derivadas).

34.2 Ressalvas

Note que minimização de funções podem somente buscar por um mínimo de cada vez. Quando houverem muitos mínimos na área de busca, o primeiro mínimo a ser encontrado irá ser retornado; todavia é difícil predizer qual dos mínimos ele irá ser. Na maioria dos casos, nenhum erro irá ser informado se você tenta encontrar um mínimo em uma área onde existe mais de de um.

Com todos os algoritmos de minimização pode ser difícil determinar a localização do mínimo com precisão numérica completa. O comportamento da função na região do mínimo x^* pode ser aproximado por uma expansão de Taylor,

34.3 Inicializando o Minimizador

Function: gsl_min_fminimizer * gsl_min_fminimizer_alloc (const gsl_min_fminimizer_type * T)

Essa função retorna um apontador para a recentemente alocada instância de um minimizador do tipo T. Por eemplo, o seguinte código cria uma instância de um minimizador por razão áurea,

const gsl_min_fminimizer_type * T 
  = gsl_min_fminimizer_goldensection;
gsl_min_fminimizer * s 
  = gsl_min_fminimizer_alloc (T);

Se não houver memória suficiente para criar o minimizador então a função retorna um apontador nulo e o controlador de erro é chamado com um código de erro de GSL_ENOMEM.

Function: int gsl_min_fminimizer_set (gsl_min_fminimizer * s, gsl_function * f, double x_minimum, double x_lower, double x_upper)

Essa função ajusta, ou zera, um minimizador já existente s para usar a função f e o intervalo inicial de busca [x_lower, x_upper], com uma suposição para a localização do mínimo x_minimum.

Se o intervalo fornecido não contiver um mínimo, então a função retorna um código de erro de GSL_EINVAL.

Function: int gsl_min_fminimizer_set_with_values (gsl_min_fminimizer * s, gsl_function * f, double x_minimum, double f_minimum, double x_lower, double f_lower, double x_upper, double f_upper)

Essa função é equivalente a gsl_min_fminimizer_set mas usa os valores f_minimum, f_lower e f_upper ao invés de calcular f(x_minimum), f(x_lower) e f(x_upper).

Function: void gsl_min_fminimizer_free (gsl_min_fminimizer * s)

Essa função libera toda a memória associada ao minimizador s.

Function: const char * gsl_min_fminimizer_name (const gsl_min_fminimizer * s)

Essa função retorna um apontador para o nome do minimizador. Por exemplo,

printf ("s é um minimizador '%s'\n",
        gsl_min_fminimizer_name (s));

pode imprimir alguma coisa como s is a minimizador 'brent'.

34.4 Fornecendo a função para minimizar

Você deve fornecer uma função contínua de uma variável para os minimizadores trabalharem sobre ela. Com o objetivo de permitir parâmetros gerais as funções são definidas como sendo do tipo de dado gsl_function (veja seção Fornecendo a função a ser resolvida).

34.5 Iteração

As seguintes funções norteiam a iteração de cada algoritmo. Cada função executa uma iteração para atualizar o estado de qualquer minimizador do tipo correspondente. As mesmas funções trabalham para todos os minimizadores de forma que diferentes métodos podem ser substituídos durante a execução do programa se modificações no código.

Function: int gsl_min_fminimizer_iterate (gsl_min_fminimizer * s)

Essa função executa uma iteração simples do minimizador s. Se a iteração encontrar um problema inesperado então um código de erro irá ser retornado,

GSL_EBADFUNC

a iteração encontrou um ponto singular onde a função avaliou para Inf ou para NaN.

GSL_FAILURE

o algoritmo não pode melhorar a melhor aproximação atual ou melhorar o limite do intervalo.

O minimizador mentém uma atual melhor estimativa da posição do mínimo em todas as vezes, e o atual limite do intervalo de mínimo. essa informação pode ser acessada com as seguintes funções auxiliares,

Function: double gsl_min_fminimizer_x_minimum (const gsl_min_fminimizer * s)

Essa função retorna a atual estimativa da posição do minimo para o minimizador s.

Function: double gsl_min_fminimizer_x_upper (const gsl_min_fminimizer * s)

Function: double gsl_min_fminimizer_x_lower (const gsl_min_fminimizer * s)

Essas funções retornam o atual limite superior e o atual limite inferior do intervalo para o minimizador s.

Function: double gsl_min_fminimizer_f_minimum (const gsl_min_fminimizer * s)

Function: double gsl_min_fminimizer_f_upper (const gsl_min_fminimizer * s)

Function: double gsl_min_fminimizer_f_lower (const gsl_min_fminimizer * s)

Essas funções retornam o valor da função na atual estimativa de valor mínimo e nos limites superior e inferior do intervalo para o minimizador s.

34.6 Parâmetros de Parada

Um procedimento de minimização deve parar quando uma das seguintes condições for verdadeira:

• Um mínimo for encontrado dentro da precisão definida pelo usuário.
• Um número máximo de iterações especificado pelo usuário foi alcançado.
• Um erro tiver ocorrido.

O ajuste dessas condições está sob o controle do usuário. A função abaixo permite testar a precisão do resultado atual.

Function: int gsl_min_test_interval (double x_lower, double x_upper, double epsabs, double epsrel)

Essa função testa a convergência do intervalo [x_lower, x_upper] com erro absoluto epsabs e erro relativo epsrel. O teste retorna GSL_SUCCESS se a seguinte condição for encontrada,

|a − b| < epsabs + epsrel   min (|a|,|b|)

quando o intervalo x = [a,b] não contiver a orígem. Se o intervalo incluir a orígem então \min(|a|,|b|) é substituído por zero (que é o menor valor de |x| no referido intervalo). Isso garante que o erro relativo é precisamente estimado para mínimos perto da orígem.

Essa condição sobre o intervalo também implica que qualquer estimativa do mínimo x_m no intervalo satisfaz a mesma condição com relação ao verdadeiro mínimo x_m^*,

|xm − xm*| < epsabs + epsrel  xm*

assumindo que o verdadeiro mínimo x_m^* esteja contido dentro do intervalo.

34.7 Algoritmos de Minimização

Os algoritmos de minimização descritos nessa seção requerem um intervalo inicial que garantidamente contém um mínimo—se a e b são extremidades do intervalo e x é uma estimativa do mínimo então f(a) > f(x) < f(b). Isso garante que a função tem ao menos um mínimo em algum lugar no intervalo. Se um intervalo inicial válido for usado então esse algoritmo não pode falhar, desde que a função seja bem comportada.

Minimizer: gsl_min_fminimizer_goldensection

O algoritmo da razão áurea é o método mais simples de delimitar o mínimo de uma função. É o mais lento algoritmo fornecido pela biblioteca, com convergência linear.

A cada iteração, o algoritmo primeiro compara os subintervalos a partir das extremidades do intervalo mínimo atual. O maior subintervalo é dividido obedecendo a razão áurea (usando a famosa razão (3-\sqrt 5)/2 = 0.3189660…) e o valor da função nesse novo ponto é calculado. O novo valor é usado com a restrição f(a') > f(x') < f(b') para um novo intervalo selecionado contendo o mínimo, fazendo o descarte do menor ponto útil. Esse procedimento pode ser continuado indefinidamente até que o intervalo seja suficientemente pequeno. Escolhendo a razão áurea como a razão de bissecção pode ser demonstrado que fornece a mais rápida convergência para esse tipo de algoritmo.

Minimizer: gsl_min_fminimizer_brent

O algoritmo de minimização de Brent combina uma interpolação parabólica com o algoritmo da razão áurea. Esse procedimento produz um algoritmo rápido que além de rápido é também robusto.

Um esboço do algoritmo pode ser sumarizado como segue: a cada iteração o método de brent aproxima a função usando uma parábola de interpolação que passa por trêns pontos exstentes. O mínimo da parábola é tomada como uma suposição para o mínimo. Se essa suposição cair dentro dos limites do intervalo atual então o ponto interpolado é aceito, e usado para gerar um intervalo menor. Se o ponto interpolado não for aceito então o algoritmo retorna para um passo de razão áurea comum. Os detalhes completos do método de Brent incluem algumas verificações adicionais para melhorar a convergência.

Minimizer: gsl_min_fminimizer_quad_golden

Essa é uma variante do algoritmo de Brent que usa o algoritmo de comprimento de passo salvaguardado de Gill e Murray.

34.8 Exemplos

O seguinte programa usa o algoritmo de Brent para encontrar o menor valor da função f(x) = \cos(x) + 1, que ocorre em x = \pi. O intervalo de início é (0,6), com uma suposição inicial para o mínimo de 2.

#include <stdio.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_min.h>

double fn1 (double x, void * params)
{
  return cos(x) + 1.0;
}

int
main (void)
{
  int status;
  int iter = 0, max_iter = 100;
  const gsl_min_fminimizer_type *T;
  gsl_min_fminimizer *s;
  double m = 2.0, m_expected = M_PI;
  double a = 0.0, b = 6.0;
  gsl_function F;

  F.function = &fn1;
  F.params = 0;

  T = gsl_min_fminimizer_brent;
  s = gsl_min_fminimizer_alloc (T);
  gsl_min_fminimizer_set (s, &F, m, a, b);

  printf ("using %s method\n",
          gsl_min_fminimizer_name (s));

  printf ("%5s [%9s, %9s] %9s %10s %9s\n",
          "iter", "lower", "upper", "min",
          "err", "err(est)");

  printf ("%5d [%.7f, %.7f] %.7f %+.7f %.7f\n",
          iter, a, b,
          m, m - m_expected, b - a);

  do
    {
      iter++;
      status = gsl_min_fminimizer_iterate (s);

      m = gsl_min_fminimizer_x_minimum (s);
      a = gsl_min_fminimizer_x_lower (s);
      b = gsl_min_fminimizer_x_upper (s);

      status 
        = gsl_min_test_interval (a, b, 0.001, 0.0);

      if (status == GSL_SUCCESS)
        printf ("Converged:\n");

      printf ("%5d [%.7f, %.7f] "
              "%.7f %+.7f %.7f\n",
              iter, a, b,
              m, m - m_expected, b - a);
    }
  while (status == GSL_CONTINUE && iter < max_iter);

  gsl_min_fminimizer_free (s);

  return status;
}

Aqui está os resultados do procedimento de minimização.

$ ./a.out 
    0 [0.0000000, 6.0000000] 2.0000000 -1.1415927 6.0000000
    1 [2.0000000, 6.0000000] 3.2758640 +0.1342713 4.0000000
    2 [2.0000000, 3.2831929] 3.2758640 +0.1342713 1.2831929
    3 [2.8689068, 3.2831929] 3.2758640 +0.1342713 0.4142862
    4 [2.8689068, 3.2831929] 3.2758640 +0.1342713 0.4142862
    5 [2.8689068, 3.2758640] 3.1460585 +0.0044658 0.4069572
    6 [3.1346075, 3.2758640] 3.1460585 +0.0044658 0.1412565
    7 [3.1346075, 3.1874620] 3.1460585 +0.0044658 0.0528545
    8 [3.1346075, 3.1460585] 3.1460585 +0.0044658 0.0114510
    9 [3.1346075, 3.1460585] 3.1424060 +0.0008133 0.0114510
   10 [3.1346075, 3.1424060] 3.1415885 -0.0000041 0.0077985
Converged:                            
   11 [3.1415885, 3.1424060] 3.1415927 -0.0000000 0.0008175

34.9 Referências e Leituras Adicionais

Informação adicional sobre o algoritmo de Brent está disponível no seguinte livro,

• Richard Brent, Algorithms for minimização without derivatives, Prentice-Hall (1973), republished by Dover in paperback (2002), ISBN 0-486-41998-3.

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.