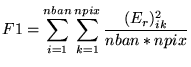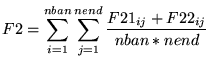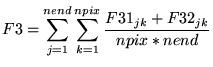Função de Avaliação - Fitness

Para calcular o erro, foi usado como base o método de restrição pelos mínimos quadrados(Constrained Least-Squares (CLS) Method) usado por Shimabukuru[13], que estima a proporção de cada componente puro (Endmember) dentro de um pixel através da minimização da soma dos quadrados dos erros. Os valores dessas proporções devem ser não negativos e eles devem somar 1 ao longo de uma banda.

Dessa forma, vamos observar que o modelo de mistura pode ser reescrito como:

$$(E_{r}) = D - RF$$ (27)

onde $R$ é a matriz de resposta espectral dos componentes de mistura que compõem a imagem calculada a partir da matriz abstrata $R_{a}$ ( $R = R_{a}T$) e $F$ é a matriz de freqüência dos componentes de mistura encontrados na matriz $R$ e $(E_{r})$ representa o erro das matrizes $R$ e $F$ obtidas com a matriz $T$ encontrada em relação à matriz $D$.

Para realizar esse cálculo, dado que i representa cada uma das bandas da matriz $D$, primeiro devemos encontrar a matriz $F$ a partir de $R$ da seguinte maneira:

$$P_{i1} = R_{i1}-R_{i3}$$ (28)

$$P_{i2} = R_{i2}-R_{i3}$$ (29)

Sendo k é a quantidade de pixels na figura analisada, temos:

$$F_{2 \times k} = \frac{P_{i \times 2}}{D_{i \times k}-(R_{i3... ...y}{cc cc} 1 \\ 1 \\ \vdots \\ 1 \\ \end{array}\right])}$$ (30)

Para garantir que as proporções de um Endmember através das bandas seja 1, calculamos:

$$F_{3k} = 1 - F_{1k} - F_{2k}$$ (31)

E dessa forma obtemos a matriz F.

Logo, o primeiro valor da função de fitness a ser minimizada pelo algoritmo deve ser:

$$F1 = \sum_{i=1}^{nban} \sum_{k=1}^{npix} \frac{(E_{r})_{ik}^{2}}{nban*npix}$$ (32)

Para tentar garantir que as proporções procuradas sejam positivas, foram incluídos valores adicionais de erro na função de minimização, com cálculo também baseado no artigo de Shimabukuru[13].

O primeiro valor consiste nos erros da matriz $R$ encontrada para valores maiores que 255 e menores que 0, pois o valor de refletância espectral de um Endmember não deve ultrapassar esses limites físicos e calcula-se da seguinte maneira:

$$F21 = R_{ij}^2$$ (33)

para todos os valores da matriz $R$ menores que zero e:

$$F22 = (R_{ij}-255)^2$$ (34)

para todos os valores da matriz $R$ maiores que 255.

Então obtemos o primeiro valor de erro adicional:

$$F2 = \sum_{i=1}^{nban} \sum_{j=1}^{nend} \frac{F21_{ij}+F22_{ij}}{nban*nend}$$ (35)

O segundo valor consiste nos erros da matriz $F$ encontrada para valores maiores que 1 e menores que 0, pois o valor da proporção de um Endmember não pode ultrapassar esse limites e consiste da seguinte maneira:

$$F31 = (F_{ij}*255)^2$$ (36)

para todos os valores da matriz $F$ menores que zero e:

$$F32 = ((F_{ij}*255)-255)^2$$ (37)

para todos os valores da matriz $F$ maiores que 1.

O valor 255 foi multiplicado para normalizar os erros calculados. Então obtemos o segundo valor de erro adicional:

$$F3 = \sum_{j=1}^{nend} \sum_{k=1}^{npix} \frac{F31_{jk}+F32_{jk}}{npix*nend}$$ (38)

Então, a função de fitness a ser minimizada deve ser:

$$F = F1 + F2 + F3$$ (39)

A Figura 5 representa o código em MATLAB que implementa a funcção de avaliação.

Figura 5: Função de fitness: nend = número de componentes de mistura; nban = número de bandas do satelite; npix = número de pixels em cada linha da matriz de dados $D$; $T$ = indivíduo a ser avaliado; $R_{a}$ = matriz abstrata a ser transformada; $D$ matriz de dados; $P$ = soma dos erros das funções F1, F2, F3; SEQ = Representa o erro calculado a partir da função F1; SERR = Representa o erro calculado a partir da função F2; SEFR = Representa o erro calculado a partir da função F3