16 Transformada Rápida de Fourier (FFTs)

Esse capítulo descreve funçẽos para executar Transformadas Rápidas de Fourier (FFTs). A bilioteca inclui rotinas de base-2 (para comprimentos que são um expoente de dois) e rotinas com radicais mistos (que trabalham com qualquer comprimento). Por eficiência existe versões separadas das rotinas para dados reais e para dados complexos. as rotinas com radicais mistos são uma reimplementação da biblioteca FFTPACK de Paul Swarztrauber. Código Fortran para FFTPACK está disponível na Netlib (FFTPACK também inclui algumas rotinas para transformadas de seno e cosseno mas essas não estão atualmente disponiveis na GSL). Para detalhes e derivações dos respectivos algoritmos consulte o documento GSL FFT Algorithms (veja seção Referências e Leituras Adicionais)

16.1 Definições Matemáticas

Transformadas Rápidas de Fourier são algoritmos eficientes para calcular a Transformada Discreta de Fourier (DFT),

Todas as funções FFT oferecem três tipos de transformada: pela direita, inversa e pela esquerda, baseada nas mesmas definições matemáticas. A definição de transformada de Fourier pela direita, x = FFT(z), é,

Em geral existem duas possíveis escolhas para o sinal da exponencial no par transformada/ transformada-inversa. GSL segue a mesma convenção que FFTPACK, usando uma exponencial negativa para a transformada pela direita. A vantagem dessa convenção é que a transformada inversa recria a função original com síntese de Fourier simples. Numerical Recipes (41) usa a conveção oposta, uma exponencial positiva na transformada adiante.

A FFT pela esquerda é simplesmente nossa terminologia para uma versão não proporcional da inversa da FFT,

16.2 FFTs de dados complexos - Visão Geral

As entradas e saídas das rotinas FFT para números complexos são vetores estáticos empacotados de números em ponto flutuante. Em um vetor estático empacotado as partes real e imaginária de cada número complexo são colocados em elementos vizinhos alternados. Por exemplo, a seguinte definição de um vetor estático empacotado de comprimento 6,

double x[3*2];
gsl_complex_packed_array data = x;

pode ser usado para manter um vetor estático de três números complexos, z[3], da seguinte forma,

data[0] = Re(z[0])
data[1] = Im(z[0])
data[2] = Re(z[1])
data[3] = Im(z[1])
data[4] = Re(z[2])
data[5] = Im(z[2])

Os índices de vetor estático para dados possuem a mesma ordenação usada na definiçção de DFT—i.e. não existe transformadas sobre índices ou permutação de dados.

Um parâmetro stride (42) permite ao usuário executar transformadas sobre os elementos z[stride*i] ao invés de z[i]. Um salto maior que 1 pode ser usado para tomar uma FFT localmente da coluna da matriz. Um salto de 1 acessa o vetor estático sem qualquer espaçamento adicional entre elementos.

Para executar uma FFT sobre um argumento vetor, tal como gsl_vector_complex * v, use as seguintes definições (sobre seus equivalentes) ao chamar as funções descritas nesse capítulo:

gsl_complex_packed_array data = v->data;
size_t stride = v->stride;
size_t n = v->size;

Para aplicações físicas é importante relembrar que o índice que aparece na DFT não corresponde diretamente a uma frequência física. Se o lapso de tempo de uma DFT for \Delta então o domínio de frequência inclui ambas as frequências positivas e negativas, dentro do intervalo de -1/(2\Delta) passando por 0 até +1/(2\Delta). As frequências positivas são armazenadas a partir do início do vetor estático até o meio, e as frequências negativas são armazenadas voltando a partir de fim do vetor estático.

Aqui está uma tabela que mostra o layout do vetor estático data, e a correspondência entre os dados no domínio do tempo z, e os dados no domínio de frequência x.

index    z               x = FFT(z)

0        z(t = 0)        x(f = 0)
1        z(t = 1)        x(f = 1/(n Delta))
2        z(t = 2)        x(f = 2/(n Delta))
.        ........        ..................
n/2      z(t = n/2)      x(f = +1/(2 Delta),
                               -1/(2 Delta))
.        ........        ..................
n-3      z(t = n-3)      x(f = -3/(n Delta))
n-2      z(t = n-2)      x(f = -2/(n Delta))
n-1      z(t = n-1)      x(f = -1/(n Delta))

Quando n for par a localização n/2 contém as frequências mais positivas e mais negativas (+1/(2 \Delta), -1/(2 \Delta)) que são equivalentes. Se n for ímpar então a estrutura geral da tabela acima ainda se aplica, mas n/2 não aparece.

16.3 Rotinas FFT Radix-2 para dados complexos

Os algoritmos de base-2 descritos nessa seção são simples e compactos, embora não necessáriamente mais eficientes. Eles usam o algoritmo de Cooley-Tukey para calcular localmente FFTs complexas para comprimentos que são um expoente de 2—nenhum armazenamento adicional é requerido. As rotinas correspondentes self-sorting e mixed-radix oferecem melhor performace às expensas de requerer espaço de trabalho adicional.

Todas as funções descritas nessa seção são declaradas no arquivo de cabeçalho ‘gsl_fft_complex.h’.

Function: int gsl_fft_complex_radix2_forward (gsl_complex_packed_array data, size_t stride, size_t n)

Function: int gsl_fft_complex_radix2_transform (gsl_complex_packed_array data, size_t stride, size_t n, gsl_fft_direction sign)

Function: int gsl_fft_complex_radix2_backward (gsl_complex_packed_array data, size_t stride, size_t n)

Function: int gsl_fft_complex_radix2_inverse (gsl_complex_packed_array data, size_t stride, size_t n)

Essas funções calculam FFTs pela direita, pela esquerda e inversa de comprimento n com salto stride, no vetor estático complexo empacotado data usando localmente o algoritmo decimal-em-tempo base-2. O comprimento da transformada n é restrita a expoentes de dois. Para a versão transform da função o argumento sign pode ser ou forward (-1) ou backward (+1).

As funções retornam um valor de GSL_SUCCESS se denhum erro for detectado, ou GSL_EDOM se o comprimento dos dados n não for um expoente de dois.

Function: int gsl_fft_complex_radix2_dif_forward (gsl_complex_packed_array data, size_t stride, size_t n)

Function: int gsl_fft_complex_radix2_dif_transform (gsl_complex_packed_array data, size_t stride, size_t n, gsl_fft_direction sign)

Function: int gsl_fft_complex_radix2_dif_backward (gsl_complex_packed_array data, size_t stride, size_t n)

Function: int gsl_fft_complex_radix2_dif_inverse (gsl_complex_packed_array data, size_t stride, size_t n)

Essas são as versões de decimação-em-frequência das funções FFT base-2.

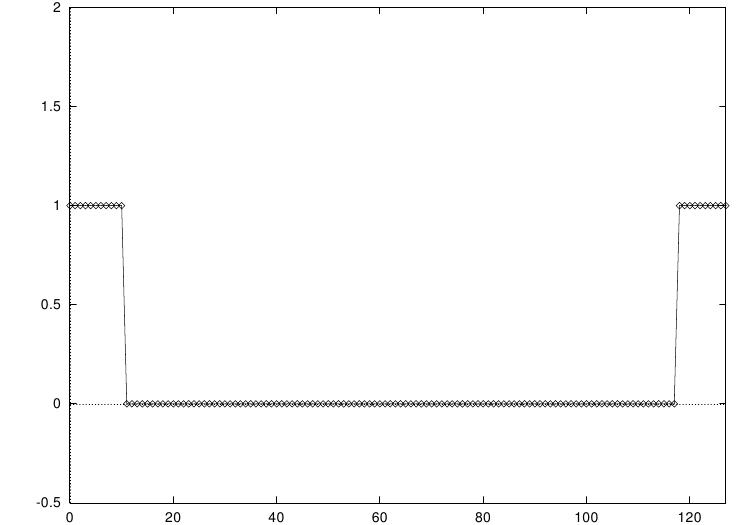
Aqui está um programa exemplo o qual calcula a FFT de pulso curto em uma amostra de comprimento 128. Para fazer a real transformada de Fourier resultante o pulso é definido para iguais tempos positivos e negativos (-10 … 10), onde os tempos negativos situam-se em torno do fim do vetor estático.

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_fft_complex.h>

#define REAL(z,i) ((z)[2*(i)])
#define IMAG(z,i) ((z)[2*(i)+1])

int
main (void)
{
  int i; double data[2*128];

  for (i = 0; i < 128; i++)
    {
       REAL(data,i) = 0.0; IMAG(data,i) = 0.0;
    }

  REAL(data,0) = 1.0;

  for (i = 1; i <= 10; i++)
    {
       REAL(data,i) = REAL(data,128-i) = 1.0;
    }

  for (i = 0; i < 128; i++)
    {
      printf ("%d %e %e\n", i, 
              REAL(data,i), IMAG(data,i));
    }
  printf ("\n");

  gsl_fft_complex_radix2_forward (data, 1, 128);

  for (i = 0; i < 128; i++)
    {
      printf ("%d %e %e\n", i, 
              REAL(data,i)/sqrt(128), 
              IMAG(data,i)/sqrt(128));
    }

  return 0;
}

Note que temos assumido que o programa está usando o controlador de erro padrão (o qual chama abort para quaisquer erros). Se você não estiver usando um controlador de erro seguro você deverá verificar a situação atual de retorno da gsl_fft_complex_radix2_forward.

Os dados transformados são ajustados novamente de forma proporcional por 1/\sqrt n de forma que se ajustem à mesma aparência da entrada. Somente a parte real é mostrada, pela escolha dos dados de entrada a parte imaginária é zero. Permitindo para a localização em torno de tempos negativos em t=128, e trabalhando em unidades de k/n, a DFT aproxima-se do continuum da transformada de Fourier, fornecendo uma função seno modulada.

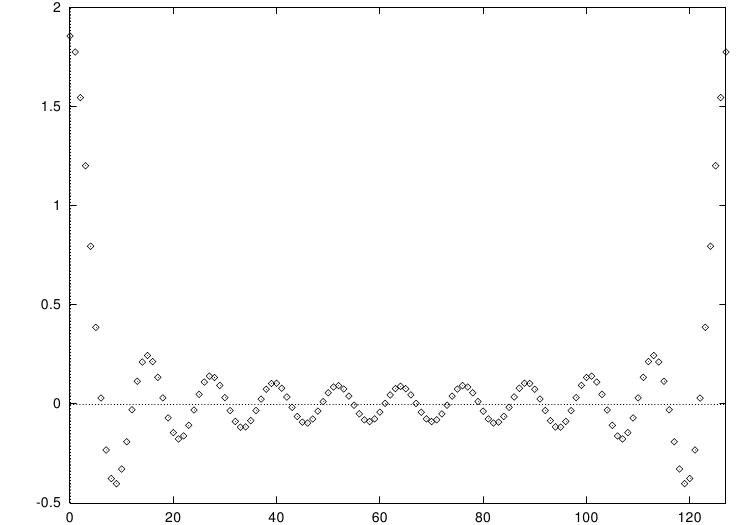
Um pulso e sua transformada discreta de Fourier, saída do programa exemplo.

16.4 Rotinas FFT Mixed-Radix para dados complexos

Essa seção descreve algoritmos FFT mixed-radix para dados complexos. As funções mixed-radix funcionam para FFTs de qualquer comprimento. Elas são uma reimplementação da biblioteca Fortran FFTPACK de Paul Swarztrauber. A teoria é explanada no artigo de revisão Self-sorting Mixed-radix FFTs de Clive Temperton. As rotinas aqui usam o mesmo esquema de indexação e algoritmos básicos usados em FFTPACK.

O algoritmo mixed-radix é baseado em módulos de subtransformadas—FFTs otimizadas de pequenos comprimentos que são conbinadas para criar grandes FFTs. Existem módulos eficientes para fatores de 2, 3, 4, 5, 6 e 7. Os módulos para fatores compostos de 4 e 6 são mais rápidos que a combinação dos módulos para 2*2 e 2*3.

Para fatores que não estão implementados como módulos existe um módulo alternativo de comprimento geral n que usa o método de Singleton para calcular eficientemente uma DFT. Esse módulo é O(n^2), é mais lento que um módulo dedicado pode ser mas trabalha para qualquer comprimento n. Certamente, comprimentos que usam o módulo de comprimento geral n irão ainda serem fatorados tanto quanto possível. Por exemplo, um comprimento de 143 irá ser fatorado em 11*13. Fatores primos grandes são o cenário de pior caso, e.g. como encontrado em n=2*3*99991, e devem ser evitados pelo fato de seu ajuste proporcioanl O(n^2) irá dominar o tempo de execução (consulte o documento GSL FFT Algorithms incluído na distribuição da GSL se você encontrar esse problema).

A função de inicialização da mixed-radix gsl_fft_complex_wavetable_alloc retorna a lista de fatores escolhidos pela biblioteca para um comprimento fornecido n. Essa função de inicialização pode ser usada para verificar como comprimento foi fatorado, e estima o tempo de execução. Para uma primeira aproximação o tempo de execução usa-se como referência n \sum f_i, onde os f_i são os fatores de n. Para programas sob controle do usuário você pode desejar emitir um alerta que a transformada irá ser lenta quando o comprimento for pobremente fatorado. Se você encontra frequêntemente comprimentos de dados que não podem ser fatorados usando os módulos para pequenos primos que existem atualmente consulte GSL FFT Algorithms para detalhes sobre adicionar suporte para outros fatores.

Todas as funções descritas nessa seção são declaradas no arquivo de cabeçalho ‘gsl_fft_complex.h’.

Function: gsl_fft_complex_wavetable * gsl_fft_complex_wavetable_alloc (size_t n)

Essa função prepara uma tabela trigonométrica de pesquisa para uma FFT complexa de comprimento n. A função retorna um apontador para a mais recentemente alocada gsl_fft_complex_wavetable se nenhum erro for detectado, e uma apontador null em caso de erro. O comprimento n é fatorado em um produto de subtransformadas, e os fatores e seus coeficientes trigonométricos estão armazenados na tabela de onda. Os coeficientes trigonométricos são calculados usado chamadas diretas a sin e a cos, por precisão. Relações recursivas podem ser usadas para calcular a tabela de pesquisa mais rapidamente, mas se uma aplicação executa muitas FFTs de mesmo comprimento então esse cálculo é um trabalho extra único que não afeta o rendimento final.

A estrutura da tabela de onda pode ser usada repetidamente para qualquer transformada de mesmo comprimento. A tabela não é modificada por chamadas a qualquer outras funções FFT. A mesma tabela de onda pode ser usada para as transformadas pela direita e pela esquerda (ou inversa) de um comprimento fornecido.

Function: void gsl_fft_complex_wavetable_free (gsl_fft_complex_wavetable * wavetable)

Essa função libera a memória associada à tabela de onda wavetable. A tabela de onda pode ser liberada se nenhuma FFT adicional de mesmo comprimento vier a ser necessária.

Essas funções operam sobre uma estrutura gsl_fft_complex_wavetable a qual contém parâmetros internos para a FFT. Não é necessário ajustar qualquer dos componentes diretamente mas pode algumas vezes ser útil examiná-los. Por exemplo, a escolha da fatoração do comprimento da FFT é dada e pode ser usada para fornecer uma estimativa do tempo de execução ou de erro numérico. A estrutura da tabela de onda é declarada no arquivo de cabeçalho ‘gsl_fft_complex.h’.

Data Type: gsl_fft_complex_wavetable

Essa é uma estrutura que mantém a fatoração e tabelas de consulta trigonométricas para o algoritmo FFT mixed radix. Tem os seguintes componentes:

size_t n

esse é o número de pontos de dados complexos

size_t nf

Esse é o número de fatores que o comprimento n foi decomposto.

size_t factor[64]

Esse é o vetor estático de fatores. Somente os primeiros nf elementos são usados.

gsl_complex * trig

Esse é um apontador para uma tabela de consulta pré-alocada de n elementos complexos.

gsl_complex * twiddle[64]

Esse é um vetor estático de apontadores em trig, fornecendo os fatores de giro para cada passo.

Os algoritmos mixed radix requerem espaço de trabalho adicional para manter os degraus intermediários da transformada.

Function: gsl_fft_complex_workspace * gsl_fft_complex_workspace_alloc (size_t n)

Essa função aloca um espaço de trabalho para uma transformada complexa de comprimento n.

Function: void gsl_fft_complex_workspace_free (gsl_fft_complex_workspace * workspace)

Essa função libera a memória associada ao espaço de trabalho workspace. O espaço de trabalho pode ser liberado se nenhum FFT adicional de mesmo tamanho for precisar desse espaço de trabalho.

As seguintes founções calculam a transformada,

Function: int gsl_fft_complex_forward (gsl_complex_packed_array data, size_t stride, size_t n, const gsl_fft_complex_wavetable * wavetable, gsl_fft_complex_workspace * work)

Function: int gsl_fft_complex_transform (gsl_complex_packed_array data, size_t stride, size_t n, const gsl_fft_complex_wavetable * wavetable, gsl_fft_complex_workspace * work, gsl_fft_direction sign)

Function: int gsl_fft_complex_backward (gsl_complex_packed_array data, size_t stride, size_t n, const gsl_fft_complex_wavetable * wavetable, gsl_fft_complex_workspace * work)

Function: int gsl_fft_complex_inverse (gsl_complex_packed_array data, size_t stride, size_t n, const gsl_fft_complex_wavetable * wavetable, gsl_fft_complex_workspace * work)

Essas funções calculam FFTs pela direita, pela esquerda e inversa de comprimento n com salto stride, sobre o vetor estático complexo empacotado data, usando um algoritmo decimação-em-frequência mixed radix. Não existe restrição sobre o comprimento n. Módulos eficientes são fornecidos para subtransformadas de comprimento 2, 3, 4, 5, 6 e 7. Quaisquer fatores restantes são calculados com um módulo lento genérico-n, O(n^2). O chamador deve fornecer uma wavetable contendo as tabelas de consulta trigonométricas e um espaço de trabalho work. Para a versão transform da função o argumento sign pode ser ou forward (-1) ou backward (+1).

As funções retornam um valor de 0 se nenhum erro for detectado. As seguintes condições gsl_errno são definidas para essas funções:

GSL_EDOM

O comprimento dos dados n não é um inteiro positivo (i.e. n é zero).

GSL_EINVAL

O comprimento dos dados n e o comprimento usado para calcular wavetable fornecida não coincidem.

Aqui está um exemplo que calcula a FFT de um pulso curto em uma amostra de comprimento (=2*3*3*5*7) usando o algoritmo mixed-radix.

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_fft_complex.h>

#define REAL(z,i) ((z)[2*(i)])
#define IMAG(z,i) ((z)[2*(i)+1])

int
main (void)
{
  int i;
  const int n = 630;
  double data[2*n];

  gsl_fft_complex_wavetable * wavetable;
  gsl_fft_complex_workspace * workspace;

  for (i = 0; i < n; i++)
    {
      REAL(data,i) = 0.0;
      IMAG(data,i) = 0.0;
    }

  data[0] = 1.0;

  for (i = 1; i <= 10; i++)
    {
      REAL(data,i) = REAL(data,n-i) = 1.0;
    }

  for (i = 0; i < n; i++)
    {
      printf ("%d: %e %e\n", i, REAL(data,i), 
                                IMAG(data,i));
    }
  printf ("\n");

  wavetable = gsl_fft_complex_wavetable_alloc (n);
  workspace = gsl_fft_complex_workspace_alloc (n);

  for (i = 0; i < wavetable->nf; i++)
    {
       printf ("# factor %d: %d\n", i, 
               wavetable->factor[i]);
    }

  gsl_fft_complex_forward (data, 1, n, 
                           wavetable, workspace);

  for (i = 0; i < n; i++)
    {
      printf ("%d: %e %e\n", i, REAL(data,i), 
                                IMAG(data,i));
    }

  gsl_fft_complex_wavetable_free (wavetable);
  gsl_fft_complex_workspace_free (workspace);
  return 0;
}

Note que temos assumido que o programa está usando o controlador de erro padrão da gsl (que chama abort para quaisquer erros). Se você não está usando um controlador de erro seguro você irá precisar verificar a situação atual de retorno de todas as rotinas gsl.

16.5 FFTs de dados reais - Visão Geral

As funções para dados reais são similares àquelas para dados complexos. Todavia, Existe uma importante diferença entre transformadas FFT pela direita e inversa. A transformada de Fourier de uma sequência real não é real. É uma sequência complexa com uma simetria especial:

Funções em gsl_fft_real calculam os coeficientes de frequência de uma sequência real. Os coeficientes meio complexos c de uma sequência real x são fornecidos pela análise de Fourier,

O arranjo preciso de armazenagem depende do algoritmo, e são diferentes para rotinas base-2 e mixed-radix. A função radix-2 opera localmente, o que limita as localizações onde cada elemento pode se armazenado. A restriçao força que as partes real e imaginárias sejam armazenadas em posições de memória não vizinhas como seria de se esperar. O algoritmo mixed-radix não tem essa restrição, e armazena as partes real e imaginárias de dado termo em localizações vizinhas (o que é desejável para melhor localização dos acessos à memória).

16.6 Rotinas FFT Radix-2 para dados reais

Essa seção descreve algoritmos FFT de base-2 para dados reais. Eles usam o algoritmo de Cooley-Tukey para calcular localmente FFTs para comprimentos que são expoentes de 2.

As funções FFT de base-2 para dados reais são declaradas nos arquivos de cabeçalho ‘gsl_fft_real.h’

Function: int gsl_fft_real_radix2_transform (double data[], size_t stride, size_t n)

Essa função calcula uma FFT base-2 localmente de comprimento n e salto stride sobre o vetor estático real data. A saída é uma sequência meio complexa, que é armazenada localmente. O arranjo dos termos meio complexos usa o seguinte esquema: para k < n/2 a parte real do k-ésimo termo é armazenada localmente na localização k, e a parte imaginária correspondente é armazenada na localização n-k. Termos com k > n/2 podem ser reconstruídos usando a simetria z_k = z^*_{n-k}. Os termos para k=0 e k=n/2 são ambos puramente real, e contam como um caso especial. Suas partes reais são armazenadas em localizações 0 e n/2 respectivamente, enquanto suas partes imaginárias que são nulas não são armazenadas.

A seguinte tabela mostra a correspondência entre a saída data e seus resultados equivalentes obtidos considerando os dados de entrada como uma sequência complexa com parte imaginária nula (assumindo stride=1),

complex[0].real    =    data[0] 
complex[0].imag    =    0 
complex[1].real    =    data[1] 
complex[1].imag    =    data[n-1]
...............         ................
complex[k].real    =    data[k]
complex[k].imag    =    data[n-k] 
...............         ................
complex[n/2].real  =    data[n/2]
complex[n/2].imag  =    0
...............         ................
complex[k'].real   =    data[k]        k' = n - k
complex[k'].imag   =   -data[n-k] 
...............         ................
complex[n-1].real  =    data[1]
complex[n-1].imag  =   -data[n-1]

Note que os dados de saída podem ser convertidos em uma sequência complexa cheia usando a função gsl_fft_halfcomplex_radix2_unpack descrita abaixo.

As funções FFT base-2 para dados meio complexos são declaradas no arquivo de cabeçalho ‘gsl_fft_halfcomplex.h’.

Function: int gsl_fft_halfcomplex_radix2_inverse (double data[], size_t stride, size_t n)

Function: int gsl_fft_halfcomplex_radix2_backward (double data[], size_t stride, size_t n)

Essas funções calculam a FFT inversa ou pela esquerda de base-2 localmente de comprimento n e salto stride sobre a sequência meio complexa data armazenada conforme o esquema de saída usado por gsl_fft_real_radix2. O rsultado é um vetor estático real armazenado em ordem natural.

Function: int gsl_fft_halfcomplex_radix2_unpack (const double halfcomplex_coefficient[], gsl_complex_packed_array complex_coefficient, size_t stride, size_t n)

Essa função converte halfcomplex_coefficient, um vetor estático de coeficientes meio complexos como retornado por gsl_fft_real_radix2_transform, em um vetor estático complexo comum, complex_coefficient. Preenche o vetor estático complexo usando a simetria z_k = z_{n-k}^* para reconstruir os elementos redundantes. O algoritmo para conversão é,

complex_coefficient[0].real 
  = halfcomplex_coefficient[0];
complex_coefficient[0].imag 
  = 0.0;

for (i = 1; i < n - i; i++)
  {
    double hc_real 
      = halfcomplex_coefficient[i*stride];
    double hc_imag 
      = halfcomplex_coefficient[(n-i)*stride];
    complex_coefficient[i*stride].real = hc_real;
    complex_coefficient[i*stride].imag = hc_imag;
    complex_coefficient[(n - i)*stride].real = hc_real;
    complex_coefficient[(n - i)*stride].imag = -hc_imag;
  }

if (i == n - i)
  {
    complex_coefficient[i*stride].real 
      = halfcomplex_coefficient[(n - 1)*stride];
    complex_coefficient[i*stride].imag 
      = 0.0;
  }

16.7 Rotinas FFT Mixed-Radix para dados reais

Essa seção descreve algoritmos FFT mixed-radix para dados reais. As funções mixed-radix funcionam para FFTs de qualquer comprimento. Elas são uma reimplementação das rotinas FFT reais na biblioteca Fortran FFTPACK por Paul Swarztrauber. A teoria por trás do algoritmo é explanada no artigo Fast Mixed-Radix Real Fourier Transforms de Clive Temperton. As rotinas aqui usam o mesmo esquema indexador e algoritmos bśicos usados em FFTPACK.

As funções usam a conveção de armazenamento da FFTPACK para sequências meio complexas. Nessa convenção a transformada meio complexa de uma sequência real é armazenada com frequências em ordem crescente, iniciando em zero, com as partes real e imaginárias de cada frequência em localizações vizinhas. Quando um valor é sabido ser real a parte imaginária não é armazenada. A parte imaginária da componente frequência-zero nunca é armazenada. É sabidamente ser zero (uma vez que a componente frequência zero é simplesmente o somatório dos dados de entrada (todos reais)). Para uma sequência de comprimento par a parte imaginária da frequência n/2 não é armazenada ou, uma vez que a simetria z_k = z_{n-k}^* implica que a sequência é puramente real também.

O esquema de armazenamento é melhor mostrado através de alguns exemplos. A tabela abaixo mostra a saída para uma sequência de elementos de comprimento ímpar, n=5. As duas colunas fornecem a correspondência entre os 5 valores na sequência meio complexa retornada por gsl_fft_real_transform, halfcomplex[] e os valores complex[] que devem ser retornados se a mesma sequência de entrada real for informada a gsl_fft_complex_backward como uma sequência complexa (com partes imaginárias ajustadas para 0),

complex[0].real  =  halfcomplex[0] 
complex[0].imag  =  0
complex[1].real  =  halfcomplex[1] 
complex[1].imag  =  halfcomplex[2]
complex[2].real  =  halfcomplex[3]
complex[2].imag  =  halfcomplex[4]
complex[3].real  =  halfcomplex[3]
complex[3].imag  = -halfcomplex[4]
complex[4].real  =  halfcomplex[1]
complex[4].imag  = -halfcomplex[2]

Os elementos altos do vetor estático complex, complex[3] e complex[4] são preenchidos usando a condição de simetria. A a parte imaginária do termo frequência zero complex[0].imag é sabidamente zero pela simetria.

A tabela adiante mostra a saída para uma sequência de comprimento par, n=6. No caso par existe dois valores para os quais são puramente reais,

complex[0].real  =  halfcomplex[0]
complex[0].imag  =  0
complex[1].real  =  halfcomplex[1] 
complex[1].imag  =  halfcomplex[2] 
complex[2].real  =  halfcomplex[3] 
complex[2].imag  =  halfcomplex[4] 
complex[3].real  =  halfcomplex[5] 
complex[3].imag  =  0 
complex[4].real  =  halfcomplex[3] 
complex[4].imag  = -halfcomplex[4]
complex[5].real  =  halfcomplex[1] 
complex[5].imag  = -halfcomplex[2] 

Os elementos altos do vetor estático complex, complex[4] e complex[5] são preenchidos usando a condição de simetria. Ambos complex[0].imag e complex[3].imag são sabidamente zero.

Todas essas funções são declaradas nos arquivos de cabeçalho ‘gsl_fft_real.h’ e ‘gsl_fft_halfcomplex.h’.

Function: gsl_fft_real_wavetable * gsl_fft_real_wavetable_alloc (size_t n)

Function: gsl_fft_halfcomplex_wavetable * gsl_fft_halfcomplex_wavetable_alloc (size_t n)

Essas funções preparam tabelas trigonométricas de consulta para uma FFT do tamanho de n elementos reais. As funções retornam um apontador para a mais recente estrutura alocada se não forem detectados erros, e um apontador nulo em caso de erro. O comprimento n é fatorado em um produto de subtransformadas, e os fatores e seus coeficientes trigonométricos são armazenados na tabela de onda. Os coeficientes trigonométricos são calculados usando chamadas diretas a sin e a cos, por precisão. Relações recursivas podem ser usadas para calcular a tabela de consulta mais rápida, mas se uma aplicação executa muitas FFTs de mesmo comprimento então o cálculo de tabela de onda é uma única sobrecarga de trabalho que não afeta o desempenho final.

A estrutura wavetable pode ser usada repetidamente para qualquer transformada de mesmo comprimento. A tabela não é modificada por chamadas a qualquer das outras funções FFT. O tipo apropriado de wavetable deve ser usado para transformadas pela direita real ou meio complexa inversa.

Function: void gsl_fft_real_wavetable_free (gsl_fft_real_wavetable * wavetable)

Function: void gsl_fft_halfcomplex_wavetable_free (gsl_fft_halfcomplex_wavetable * wavetable)

Essas funções libera a memória associada à tabela de onda wavetable. A tabela de onda pode ser liberado se nenhuma FFT adicional de mesmo comprimento for ser necessária.

Os algoritmos mixed radix requerem espaço de trabalho adicional para manter os passos intermediários da transformada,

Function: gsl_fft_real_workspace * gsl_fft_real_workspace_alloc (size_t n)

Essa função aloca um espaço de trabalho para uma transformada real de comprimento n. O mesmo espaço de trabalho pode ser usado para ambas as transformadas pela direita real e meio complexa inversa.

Function: void gsl_fft_real_workspace_free (gsl_fft_real_workspace * workspace)

Essa função libera a memória associada ao espaço de trabalho workspace. O espaço de trabalho pode ser liberado se nenhuma FFT adicional de mesmo comprimento for ser necessária.

As seguintes funções calculam a transformada de dados reais e meio complexos,

Function: int gsl_fft_real_transform (double data[], size_t stride, size_t n, const gsl_fft_real_wavetable * wavetable, gsl_fft_real_workspace * work)

Function: int gsl_fft_halfcomplex_transform (double data[], size_t stride, size_t n, const gsl_fft_halfcomplex_wavetable * wavetable, gsl_fft_real_workspace * work)

Essas funções calculam a FFT dos dados armazenados em data, um vetor estático real ou meio complexo de comprimento n, usando um algoritmo mixed radix de decimação-em-frequência. Para gsl_fft_real_transform data é um vetor estático de dados reais ordenados em função do tempo. Para gsl_fft_halfcomplex_transform data contém coeficientes de Fourier na ordenação meio complexa descrita acima. Não existe restrição sobre o comprimento n. Módulos eficientes são fornecidos para subtransformadas de comprimento 2, 3, 4 e 5. Quaisquer fatores restantes são calculados com um módulo geral, O(n^2), que é lento. O chamador deve fornecer uma wavetable contendo tabela de consultas trigonométricas e um espaço de trabalho work.

Function: int gsl_fft_real_unpack (const double real_coefficient[], gsl_complex_packed_array complex_coefficient, size_t stride, size_t n)

Essa função converte um vetor estático real simples, real_coefficient em um vetor estático complexo equivalente, complex_coefficient, (com a parte imaginária ajustada para zero), adequado para rotinas gsl_fft_complex. O algoritmo para a conversão é simplesmente,

for (i = 0; i < n; i++)
  {
    complex_coefficient[i*stride].real 
      = real_coefficient[i*stride];
    complex_coefficient[i*stride].imag 
      = 0.0;
  }

Function: int gsl_fft_halfcomplex_unpack (const double halfcomplex_coefficient[], gsl_complex_packed_array complex_coefficient, size_t stride, size_t n)

Essa função converte halfcomplex_coefficient, um vetor estático de coeficientes meio complexos como retornado por gsl_fft_real_transform, em um vetor estático complexo, complex_coefficient. Preenche o vetor estático complexos usando a simetria z_k = z_{n-k}^* para reconstruir elementos redundantes. O algoritmo para a conversão é,

complex_coefficient[0].real 
  = halfcomplex_coefficient[0];
complex_coefficient[0].imag 
  = 0.0;

for (i = 1; i < n - i; i++)
  {
    double hc_real 
      = halfcomplex_coefficient[(2 * i - 1)*stride];
    double hc_imag 
      = halfcomplex_coefficient[(2 * i)*stride];
    complex_coefficient[i*stride].real = hc_real;
    complex_coefficient[i*stride].imag = hc_imag;
    complex_coefficient[(n - i)*stride].real = hc_real;
    complex_coefficient[(n - i)*stride].imag = -hc_imag;
  }

if (i == n - i)
  {
    complex_coefficient[i*stride].real 
      = halfcomplex_coefficient[(n - 1)*stride];
    complex_coefficient[i*stride].imag 
      = 0.0;
  }

Aqui está um programa exemplo usando gsl_fft_real_transform e gsl_fft_halfcomplex_inverse. Gera um sinal real com a aparência de um pulso quadrado. O pulso é transformado via Fourier para o espaço frequência, e todo o resto com exceção das dez menores componentes de frequência que são removidas pelo vetor estático de coeficientes de Fourier retornados por gsl_fft_real_transform.

Os restantes coeficientes de Fourier são transformados de volta para o domínio tempo, para fornecer uma versão filtrada do pulso quadrado. Uma vez que coeficientes de Fourier são armazenados usando simetria meio complexa ambas as frequências positiva e negativa são removidas e o sinal filtrado final é também real.

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_fft_real.h>
#include <gsl/gsl_fft_halfcomplex.h>

int
main (void)
{
  int i, n = 100;
  double data[n];

  gsl_fft_real_wavetable * real;
  gsl_fft_halfcomplex_wavetable * hc;
  gsl_fft_real_workspace * work;

  for (i = 0; i < n; i++)
    {
      data[i] = 0.0;
    }

  for (i = n / 3; i < 2 * n / 3; i++)
    {
      data[i] = 1.0;
    }

  for (i = 0; i < n; i++)
    {
      printf ("%d: %e\n", i, data[i]);
    }
  printf ("\n");

  work = gsl_fft_real_workspace_alloc (n);
  real = gsl_fft_real_wavetable_alloc (n);

  gsl_fft_real_transform (data, 1, n, 
                          real, work);

  gsl_fft_real_wavetable_free (real);

  for (i = 11; i < n; i++)
    {
      data[i] = 0;
    }

  hc = gsl_fft_halfcomplex_wavetable_alloc (n);

  gsl_fft_halfcomplex_inverse (data, 1, n, 
                               hc, work);
  gsl_fft_halfcomplex_wavetable_free (hc);

  for (i = 0; i < n; i++)
    {
      printf ("%d: %e\n", i, data[i]);
    }

  gsl_fft_real_workspace_free (work);
  return 0;
}

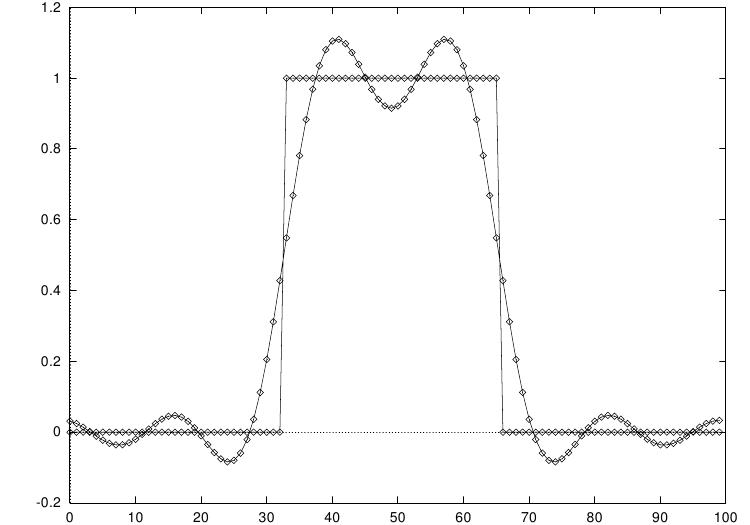
Versão passa-baixa filtrada de um pulso real, saída do programa exemplo.

16.8 Referências e Leituras Adicionais

Um bom ponto de partida para aprender mais sobre a FFT é o artigo de revisão Fast Fourier Transform: A Tutorial Review and A State of the Art por Duhamel e Vetterli,

• P. Duhamel and M. Vetterli. Fast Fourier transforms: A tutorial review and a state of the art. Signal Processing, 19:259–299, 1990.

Para descobrir mais informações sobre os algoritmos usados nas rotinas da GSL você pode desejar consultar o documento GSL FFT Algorithms (está incluído na GSL, como ‘doc/fftalgorithms.tex’). Tem informações gerais sobre FFTs e derivação explícita da implementação para cada rotina. Exisste também referências à literatura relemvante. Por conveniência algumas ou mais importantes referências são reproduzidas abaixo.

Existem muitos livros introdutórios sobre FFT com programas exemplo, tais como The Fast Fourier Transform por Brigham e DFT/FFT and Convolution Algorithms por Burrus e Parks,

• E. Oran Brigham. The Fast Fourier Transform. Prentice Hall, 1974.
• C. S. Burrus and T. W. Parks. DFT/FFT and Convolution Algorithms. Wiley, 1984.

Ambos esses livros introdutórios abrangem o FFT base-2 em algum detalhe. O algoritmo mixed-radix no coração das rotinas FFTPACK é revisado no artigo de Clive Temperton,

• Clive Temperton. Self-sorting mixed-radix fast Fourier transforms. Journal of Computational Physics, 52(1):1–23, 1983.

A derivação de FFTs para dados reais é explanada nos seguintes dosi atigos,

• Henrik V. Sorenson, Douglas L. Jones, Michael T. Heideman, and C. Sidney Burrus. Real-valued fast Fourier transform algorithms. IEEE Transactions on Acoustics, Speech, and Signal Processing, ASSP-35(6):849–863, 1987.
• Clive Temperton. Fast mixed-radix real Fourier transforms. Journal of Computational Physics, 52:340–350, 1983.

Em 1979 o IEEE publicou um compêndio de cuidadosa revisão de programas FFT em Fortran no Programs for Digital Signal Processing. É uma referência útil para implementações de muitos diferentes algoritmos FFT,

• Digital Signal Processing Committee and IEEE Acoustics, Speech, and Signal Processing Committee, editors. Programs for Digital Signal Processing. IEEE Press, 1979.

Para trabalho em larga escala com FFT recomendamos o uso da bibliote FFT dedicada por Frigo e Johnson. A biblioteca FFTW é auto-otimizada—automaticamente ajusta-se a si mesma para cada plataforma de hardware com o objetivo de alcançar a máxima performace. Está disponível sob a GNU GPL.

• FFTW Website, http://www.fftw.org/

O código fonte para FFTPACK está disponível a partir da Netlib,

• FFTPACK, http://www.netlib.org/fftpack/

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.