19 Sequências quase aleatórias

Esse capítulo descreve funções para geração de sequências quase aleatórias em dimensões arbitrárias. Uma sequência quase aleatória progressivamente abrange um espaço d-dimensional com um conjunto de pontos que são uniformemente distribuídos. Sequências quase aleatórias são também conhecidas com sequências de baixa discrepância. Os geradores de sequência quase aleatória usam uma interface que é similar à interface para geradores de números aleatórios, exceto que a semeadura não é requerida—cada gerador produz uma sequência simples.

As funções descritas nessa seção são declaradas no arquivo de cabeçalho ‘gsl_qrng.h’.

19.1 Inicialização de gerador de números quase aleatórios

Function: gsl_qrng * gsl_qrng_alloc (const gsl_qrng_type * T, unsigned int d): Essa função retorna um apontador para uma instância recentemente criada de um gerador de sequência quase aleatória do tipo T e dimensão d. Se não houver memória suficiente para criar o gerador então a função retorna um apontador nulo e o controlador de erro é chamado com um código de erro de GSL_ENOMEM.

Function: void gsl_qrng_free (gsl_qrng * q): Essa função libera toda a memória associada ao gerador q.

Function: void gsl_qrng_init (gsl_qrng * q): Essa função reinicializa o gerador q para seu pointo de início. Note que sequências quase aleatórias não usam uma semente e sempre produzem o mesmo conjunto de valores.

19.2 Fazendo amostragem a partir de um gerador de números quase aleatórios

Function: int gsl_qrng_get (const gsl_qrng * q, double x[]): Essa função armazena o ponto seguinte a partir do gerador de sequência q no vetor estático x. O espaço disponível para x deve coincidir com a dimensão do gerador. O ponto x irá localizar-ser no intervalo 0 < x_i < 1 para cada x_i. Uma versão modificada dessa função é usada quando HAVE_INLINE for definida.

19.3 Funções auxiliares aos geradores de números quase aleatórios

Function: const char * gsl_qrng_name (const gsl_qrng * q): Essa função retorna um apontador para o nome do gerador.

Function: size_t gsl_qrng_size (const gsl_qrng * q)

Function: void * gsl_qrng_state (const gsl_qrng * q)

Essa função retorna um apontador para o estado do gerador r e seu tamanho. Você pode usar essa informação para acessar o estado diretamente. Por exemplo, o seguinte código irá escrever o estado de um gerador para um fluxo,

void * state = gsl_qrng_state (q);
size_t n = gsl_qrng_size (q);
fwrite (state, n, 1, stream);

19.4 Gravando e Reordenando o estado do gerador de números quase aleatórios

Function: int gsl_qrng_memcpy (gsl_qrng * dest, const gsl_qrng * src): Essa função copia o gerador de sequência quase aleatória src para o gerador pré-existente dest, fazendo de dest uma cópia exata de src. Os dois geradores devem ser do mesmo tipo.

Function: gsl_qrng * gsl_qrng_clone (const gsl_qrng * q): Essa função retorna um apontador para um mais recentemente criado gerador que é uma cópia exata do gerador q.

19.5 Algoritmos de geradores de números quase aleatórios

Os seguintes algoritmos de sequência quase aleatória estão disponíveis,

Generator: gsl_qrng_niederreiter_2: Esse gerador usa o algoritmo descrito em Bratley, Fox, Niederreiter, ACM Trans. Model. Comp. Sim. 2, 195 (1992). É válido até 12 dimensões.

Generator: gsl_qrng_sobol: Esse gerador usa a sequência de Sobol descrita em Antonov, Saleev, USSR Comput. Maths. Math. Phys. 19, 252 (1980). É válido até 40 dimensões.

Generator: gsl_qrng_halton
Generator: gsl_qrng_reversehalton: Esses geradores usam as sequências de Halton e reversa de Halton descritas em J.H. Halton, Numerische Mathematik 2, 84-90 (1960) e B. Vandewoestyne e R. Cools Computational and Applied Mathematics 189, 1&2, 341-361 (2006). Eles são válidos até 1229 dimensões.

19.6 Exemplos

O seguinte programa mostra na tela os primeiros 1024 pontos da sequência 2-dimensional de Sobol.

#include <stdio.h>
#include <gsl/gsl_qrng.h>

int
main (void)
{
  int i;
  gsl_qrng * q = gsl_qrng_alloc (gsl_qrng_sobol, 2);

  for (i = 0; i < 1024; i++)
    {
      double v[2];
      gsl_qrng_get (q, v);
      printf ("%.5f %.5f\n", v[0], v[1]);
    }

  gsl_qrng_free (q);
  return 0;
}

Aqui está a saída do programa,

$ ./a.out
0.50000 0.50000
0.75000 0.25000
0.25000 0.75000
0.37500 0.37500
0.87500 0.87500
0.62500 0.12500
0.12500 0.62500
....

Pode ser visto que pontos sucessivos progressivamente preenchem os espaços entre os pontos anteriores.

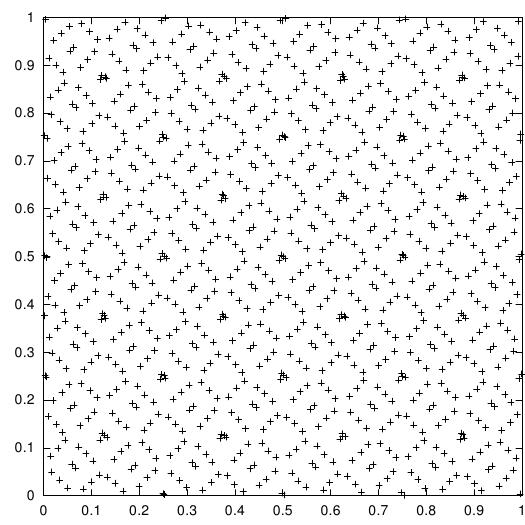
O seguinte gráfico mostra a distribuição no plano x-y dos primeiros 1024 pontos da sequência de Sobol,

Distribuição dos primeiros 1024 pontos da sequência quase aleatória de Sobol

19.7 Referências

As implementações de rotinas de sequência quase aleatória são baseadas nos algoritmos descritos no seguinte artigo,

P. Bratley and B.L. Fox and H. Niederreiter, “Algorithm 738: Programs to Generate Niederreiter’s Low-discrepancy Sequences”, ACM Transactions on Mathematical Software, Vol. 20, No. 4, Dezembro, 1994, p. 494–495.

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.