| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse capítulo descreve funções para geração de um conjunto de valores aleatórios e o cálculo de suas distribuições de probabilidade. Amostras das distribuições descritas nesse capítulo podem ser obtidas usando quaisquer dos geradores de números aleatórios na biblioteca como um código básico de aleatoriedade.
No mais simples dos casos uma distribuição não uniforme pode ser obtida analiticamente a partir da distribuição uniforme de um gerador de números aleatórios aplicando uma transformação apropriada. Esse método usa uma chamada ao gerador de números aleatórios. Distribuições mais complicadas são criadas pelo método aceitação-rejeição, que compara a desejada distribuição frente a uma distribuição que é similar e conhecida analiticamente. Isso comumente requer muitas amostras do gerador.
A biblioteca também fornece funções de distribuição acumulada e funções de distribuição acumulada inversa, algumas vezes referenciadas como funções quantil. As funções de distribuições acumuladas e suas inversas são calculadas separadamente para as caudas alta e baixa da distribuição, permitindo que precisão completa seja mantidas para pequenos resultados.
As funções para um conjunto de valores aleatórios e funções de densidade de probabilidade descritas nessa seção são declaradas em ‘gsl_randist.h’. As corespondentes funções de distribuições acumuladas são declaradas em ‘gsl_cdf.h’.
Note que as funções discretas para um conjunto de valores aleatórios sempre
retornam um valor de tipo unsigned int, e sobre a maioria das plataformas esse unsigned int
tem um valor máximo de 2^32-1 ~=~ 4.29e9. Essas funções discretas devem somente serem chamadas com
um intervalo seguro de parâmetros (onde existe uma probabilidade negligenciável de
um conjunto de valores aleatórios exceder esse limite) para prevenir resultados incorretos devido a
overflow.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Distribuições numéricas aleatórias contínuas são definidas por uma função de densidade de probabilidade, p(x), tal que a probabilidade de x ocorrer no intervalo infinitesimal de x a x+dx é p dx.
A função de distribuição acumulada para a cauda baixa P(x)
é definida pela integral,
|
A função de distribuição acumulada para a cauda alta Q(x) é
definida pela integral,
|
As funções de distribuição acumulada para as caudas alta e baixa são relacionadas através de P(x) + Q(x) = 1 e satisfazem 0 <= P(x) <= 1, 0 <= Q(x) <= 1.
The distribuições inversas acumuladas, x=P^{-1}(P) e x=Q^{-1}(Q) fornecem os valores de x que correspondem a um valor específico de P ou Q. Elas podem ser usadas para encontrar limites de confidência a partir de valores de probabilidade.
Para distribuições discretas a probabilidade de amostragem do valor
inteiro k é fornecida através de p(k), onde \sum_k p(k) = 1.
A distribuição acumulada para a cauda baixa P(k) de uma
distribuição discreta é definida como,
|
A distribuição acumulada para a cauda alta de uma distribuição
discreta Q(k) é definida como
|
Se o intervalo da distribuição for de 1 a n inclusive então P(n)=1, Q(n)=0 enquanto P(1) = p(1), Q(1)=1-p(1).
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
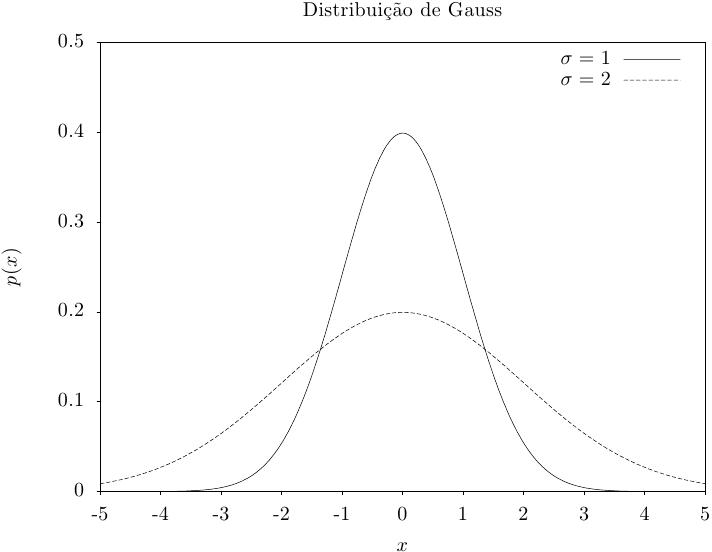
Essa função retorna um conjunto de valores aleatórios de Gauss, com média zero e
desvio padrão sigma. A distribuição de probabilidade para
um conjunto de valores de Gauss é,
|
gsl_ran_gaussian para obter uma distribuiçãod e Gauss com média
\mu. Essa função usa o algoritmo de Box-Muller que requer duas
chamadas ao gerador de números aleatórios r.
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Gauss com desvio padrão sigma, usando a fórmula fornecida acima.

Essa função calcula um conjunto de valores aleatórios de Gauss usando os métodos alternativo do zigurate de Marsaglia-Tsang e da razão de Kinderman-Monahan-Leva. O algoritmo de zigurate é o algoritmos disponível mais rápido na maioria dos casos.
essas funçãoes calculam resultados para a distribuição unitária de Gauss. Elas são equivalentes às funções acima com um desvio padrão de um, sigma = 1.
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Gauss com desvio padrão sigma.
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição unitária de Gauss.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função fornece um conjunto de valores aleatórios a partir da cauda alta de uma distribuição de Gauss com desvio padrão sigma. Os valores retornados são maiores que o limite inferior a, que deve ser positivo. O método é baseado no famoso algoritmo cauda cunha retângulo de Marsaglia (Ann. Math. Stat. 32, 894–899 (1961)), com esse aspecto explanado em Knuth, v2, 3a. ed, p139,586 (exercício 11).
A distribuição de probabilidade para um conjunto de valores aleatórios em forma de cauda de Gauss é,
|
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição em cauda de Gauss com desvio padrão sigma e limite inferior a, usando a fórmula fornecida acima.
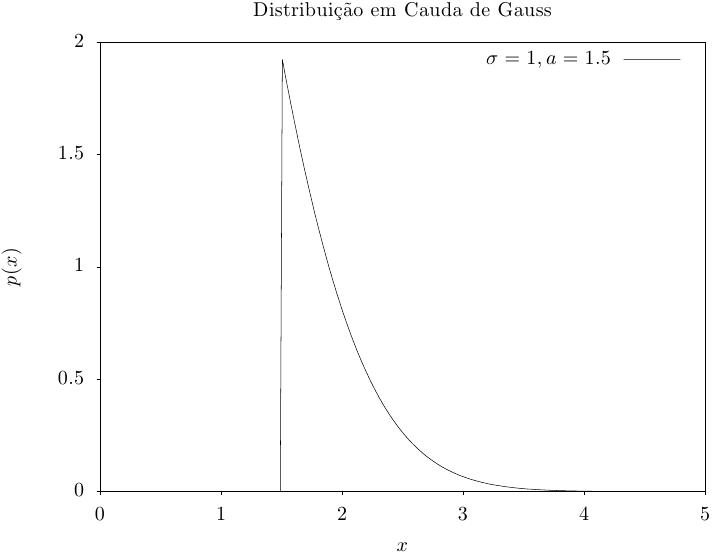
Essas funções calculam resultados para a cauda de uma distribuição unitária de Gauss. Elas são equivalentes às funções acima com um desvio padrão de um, sigma = 1.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
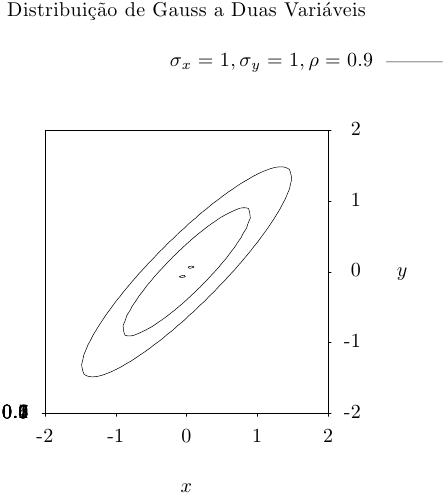
Essa função gera um par de conjuntos de valores de Gauss correlacionados, com
média zero, coeficiente de correlação rho e desvio padrão
sigma_x e sigma_y nas direções x e y.
A distribuição de probabilidade para um conjunto de valores aleatórios de Gauss a duas variáveis é,
|
Essa função calcula a densidade de probabilidade p(x,y) em (x,y) para uma distribuição de Gauss a duas variáveis com desvio padrão sigma_x, sigma_y e coeficiente de correlação rho, usando a fórmula fornecida acima.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição exponencial
com média mu. A distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição exponencial com média mu, usando a fórmula fornecida acima.

Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição exponencial com média mu.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir de uma distribuição de Laplace
com largura a. A distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Laplace com largura a, usando a fórmula fornecida acima.
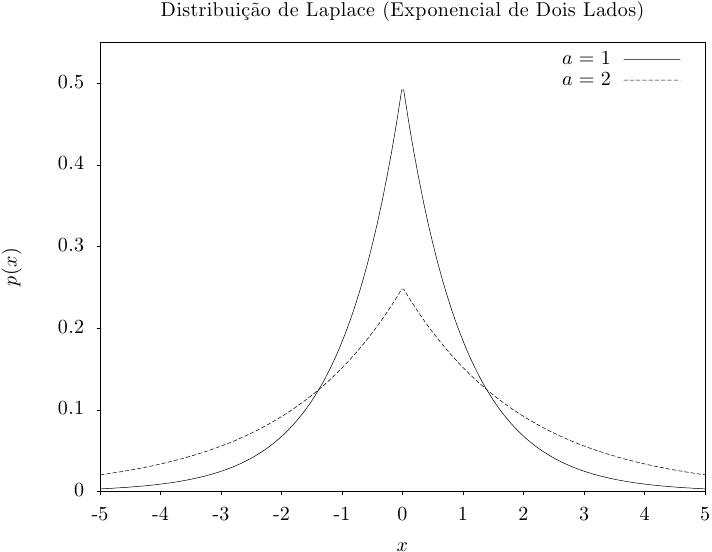
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Laplace com largura a.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição exponencial potência
com parâmetro de ajuste proporcional a e expoente b. A distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para distribuição de potência exponencial com parâmetro de ajuste proporcional a e expoente b, usando a fórmula fornecida acima.
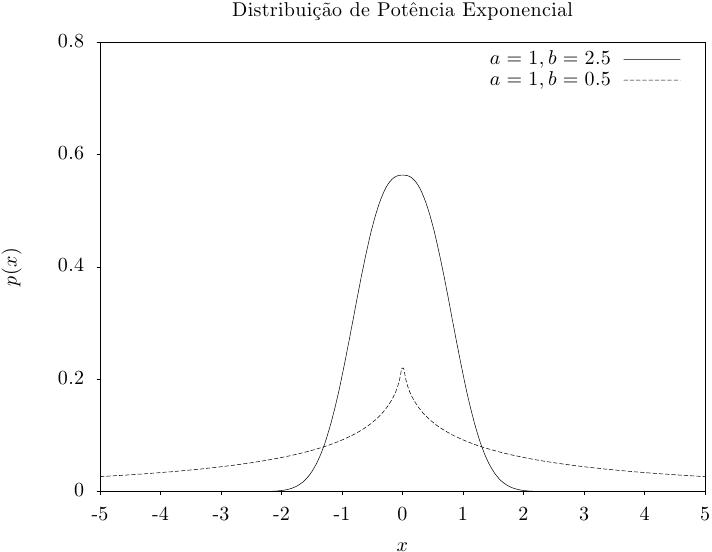
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) para a distribuição de potência exponencial com parâmetros a e b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição de Cauchy com
parâmetro de ajuste proporcional a. A distribuição de probabilidade para um conjunto de valores
aleatórios de Cauchy é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Cauchy com parâmetro de ajuste proporcional a, usando a fórmula fornecida acima.
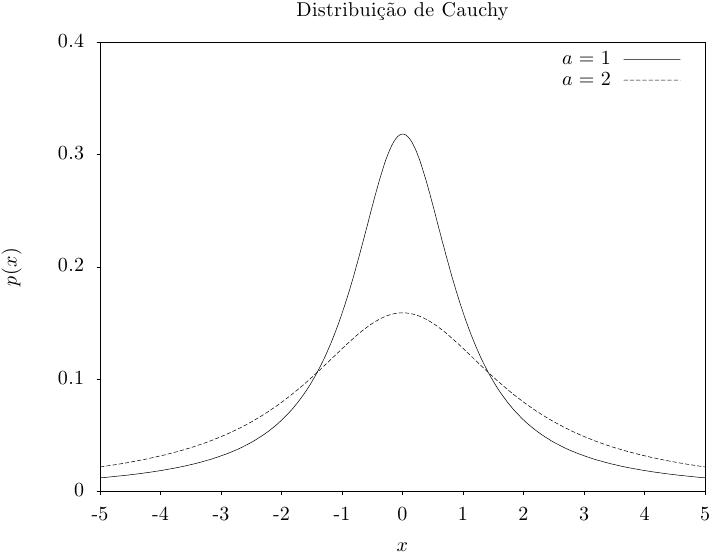
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Cauchy com parâmetro de ajuste proporcional a.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir de uma distribuição de Rayleigh com
parâmetro de ajuste proporcional sigma. A distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Rayleigh com parâmetro de ajuste proporcional sigma, usando a fórmula fornecida acima.
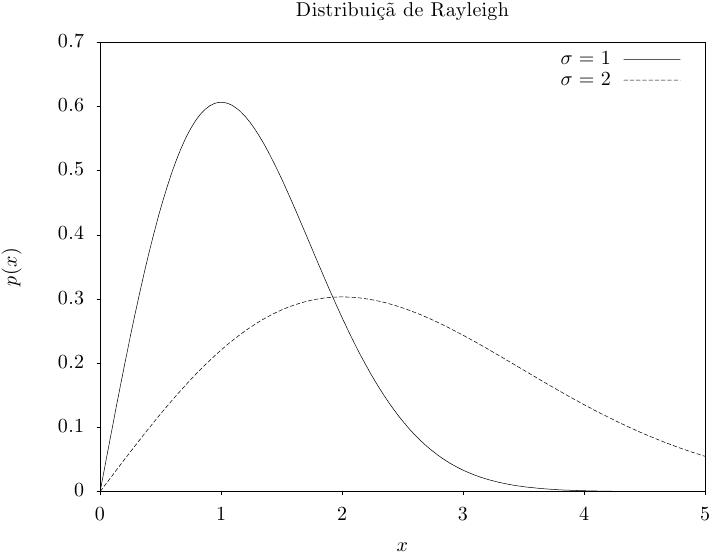
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Rayleigh com parâmetro de ajuste proporcional sigma.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
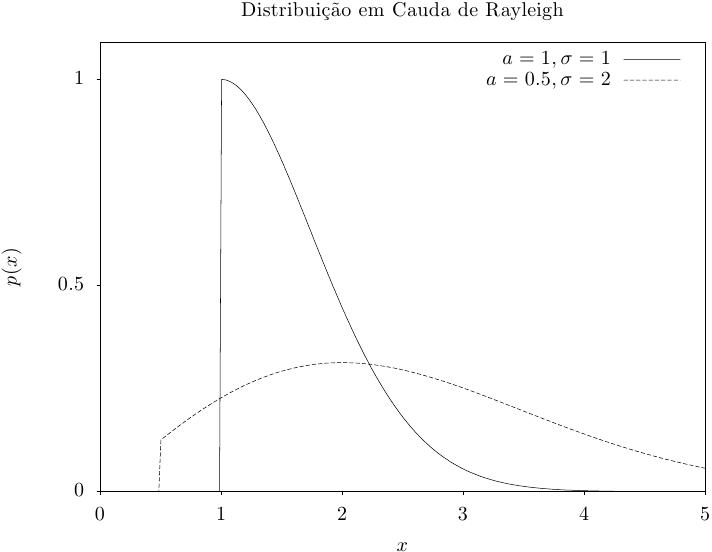
Essa função retorna um conjunto de valores aleatórios a partir da cauda da distribuição de
Rayleigh com parâmetro de ajuste proporcional sigma e um limite inferior
a. A distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição em forma de cauda de Rayleigh com parâmetro de juste proporcional sigma e limite inferior a, usando a fórmula fornecida acima.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir de um distribuição de Landau. A
distribuição de probabilidade para um conjunto de valores aleatórios de Landau é definida
analiticamente pela integral complexa,
|
|
Essa função calcula a densidade de probabilidade p(x) em x para a distribuição de Landau usando uma aproximação para a fórmula fornecida acima.
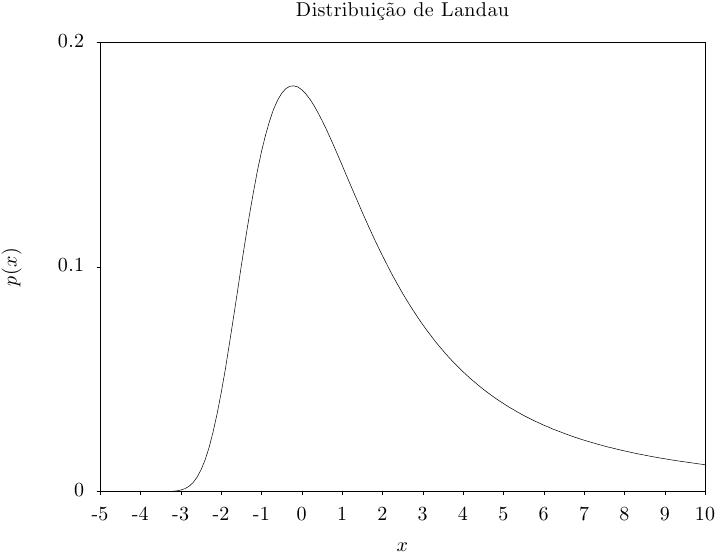
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir de uma distribuição estável
simétrica de Levy com ajuste proporcional c e expoente alpha. A distribuição
de probabilidade estável simétrica é definida através de uma transformação de Fourier,
|
pdf. Para
\alpha = 1 a distribuição se reduz à distribuição de Cauchy. Para
\alpha = 2 é uma distribuição de Gauss com \sigma = \sqrt{2} c. Para \alpha < 1 a cauda da
distribuição torna-se extremamente comprida.
O algoritmo somente funciona para 0 < alpha <= 2.
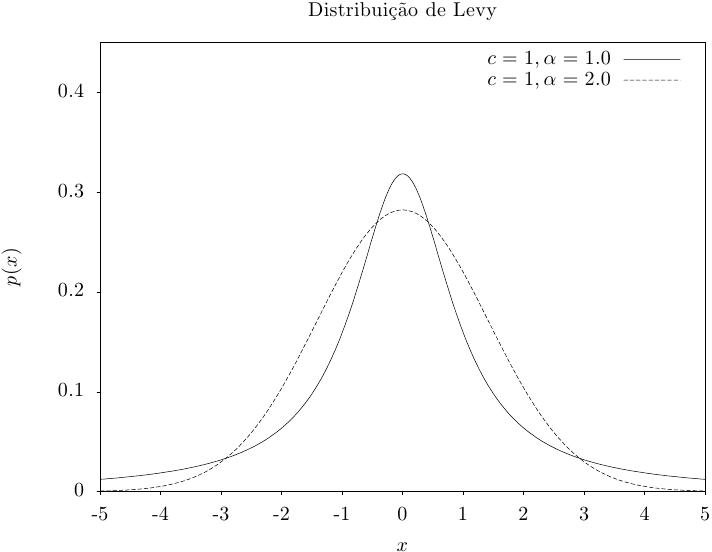
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição estável irregular
de Levy com ajuste proporcional c, expoente alpha e parâmetro de
distorção beta. O parâmetro de distorção deve estar no intervalo
[-1,1]. A distribuição de probabilidade estável irregular de Levy é definida
pela transformação de Fourier,
|
pdf (44). Para \alpha = 2 a distribuição reduz-se à distribuição
de Gauss com \sigma = \sqrt{2} c e o parâmetro de distorção não tem efeito.
Para \alpha < 1 as caudas da distribuição tornam-se extremamente
compridas. A distribuição simétrica corresponde a \beta =
0.
O algoritmo somente funciona para 0 < alpha <= 2.
As distribuições estáveis alfa de Levy possuem a propriedade de que se o conjunto de valores aleatórios estáveis alfa N são desenhados a partir da distribuição p(c, \alpha, \beta) então o somatório Y = X_1 + X_2 + \dots + X_N irá também ser distribuído como um conjunto de valores aleatórios estáveis alfa, p(N^(1/\alpha) c, \alpha, \beta).
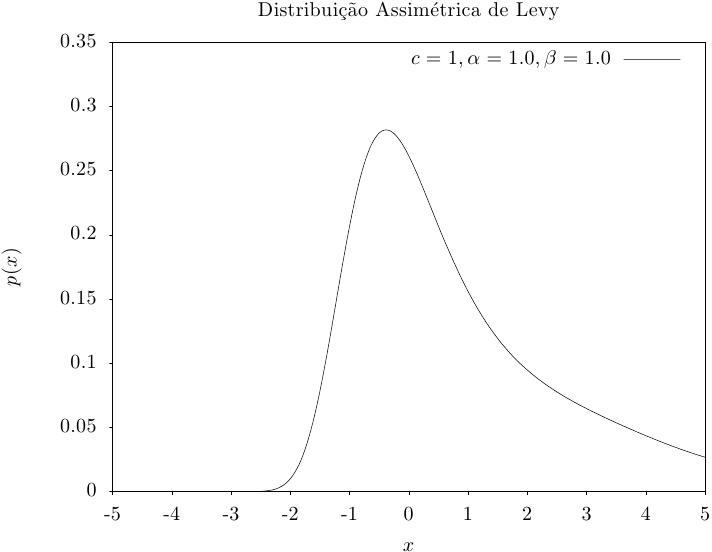
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição
gama. A função de distribuição é,
|
A distribuição gama com um parâmetro inteiro a é conhecida como a distribuição de Erlang.
O conjunto de valores aleatórios são calculados usando o método gama rápido de Marsaglia-Tsang.
Essa função para esse método foi antigamente chamada de
gsl_ran_gamma_mt e pode ainda ser acessada usando esse nome.
Essa função retorna um conjunto de valores aleatórios gama usando o algoritmo de Knuth (vol 2).
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição gama com parâmetros a e b, usando a fórmula fornecida acima.
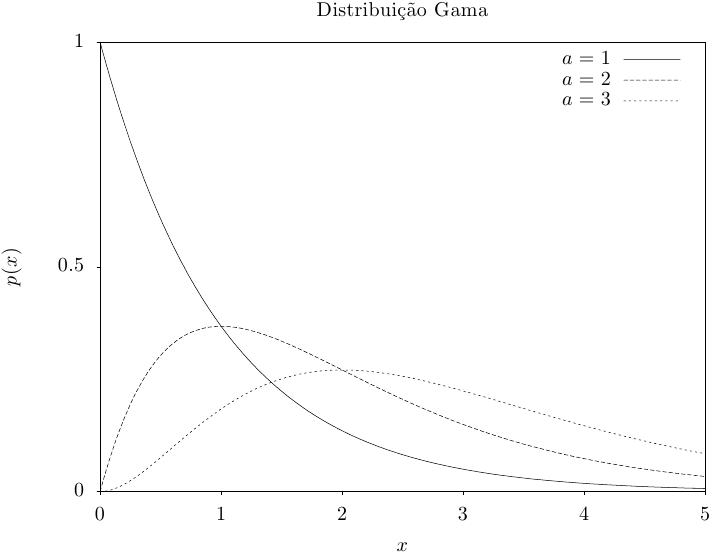
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição gama com parâmetros a e b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição
uniforme de a até b. A distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição uniforme de a a b, usando a fórmula fornecida acima.
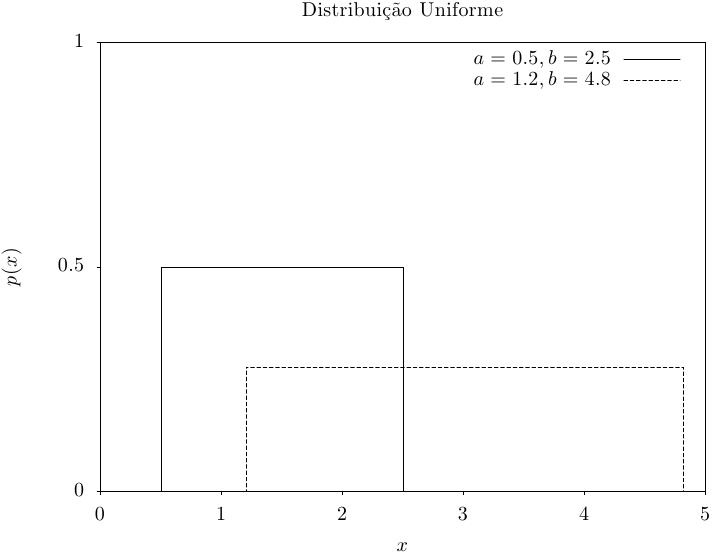
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para uma distribuição uniforme de a a b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição
lognormal. A função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição lognormal com parâmetros zeta e sigma, usando a fórmula fornecida acima.
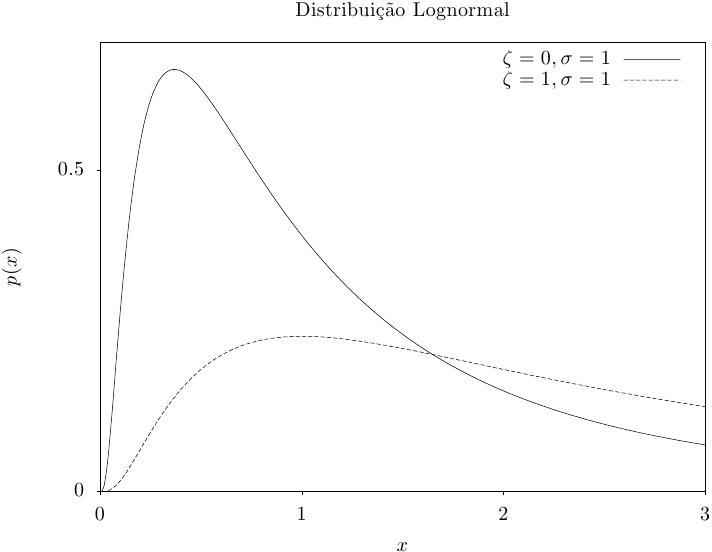
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição lognormal com parâmetros zeta e sigma.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
A distribuição chi-quadrada aparece em estatísticas. Se Y_i forem
n conjuntos de valores aleatórios de Gauss independentes com variância unitária então as
somas de quadrados,
|
Essa função retorna um conjunto de valores aleatórios a partir da distribuição chi-quadrada
com nu graus de liberdade. A função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição chi-quadrada com nu graus de liberdade, usando a fórmula fornecida acima.
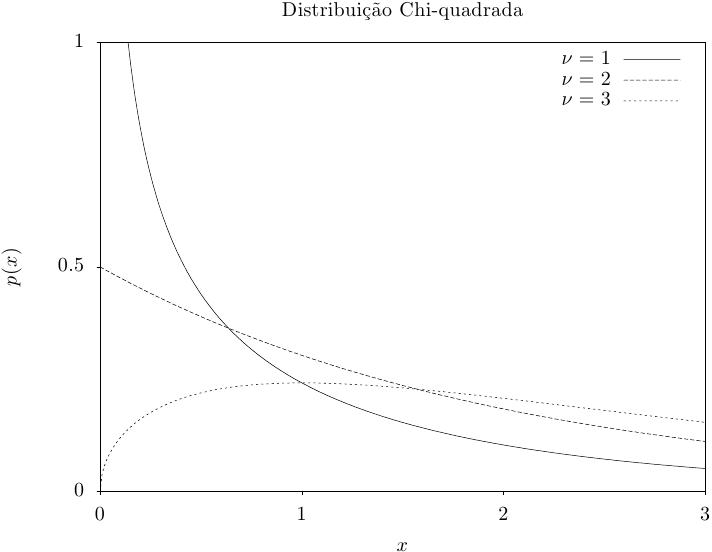
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição chi-quadrada com nu graus de liberdade.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
A distribuição F aparece em estatísticas. Se Y_1 e Y_2
forem divergentes de forma chi-quadrada com \nu_1 e \nu_2 graus de
liberdade então a razão,
|
Essa função retorna um conjunto de valores aleatórios a partir da distribuição F com graus de liberdade nu1 e nu2. A função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição F com nu1 e nu2 graus de liberdade, usando a fórmula fornecida acima.
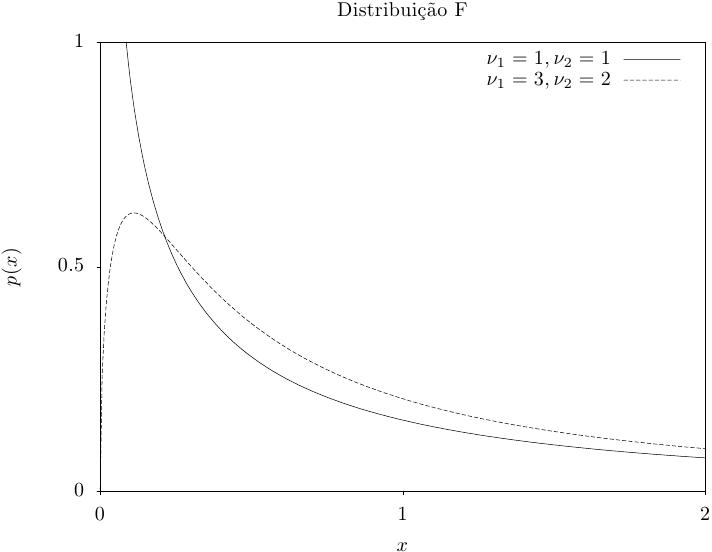
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição F com nu1 e nu2 graus de liberdade.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
A distribuição t aparece em estatísticas. Se Y_1 tem uma distribuição
normal e Y_2 tem uma distribuição chi-quadrada com
\nu graus de liberdade então a razão,
|
Essa função retorna um conjunto de valores aleatórios a partir da distribuição t. A
função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição t com nu graus de liberdade, usando a fórmula fornecida acima.
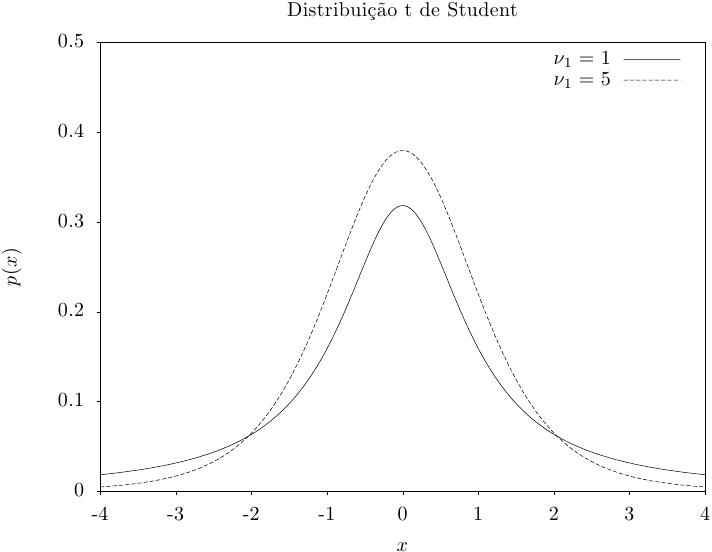
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição t com nu graus de liberdade.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição
beta. A função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição beta com parâmetros a e b, usando a fórmula fornecida acima.
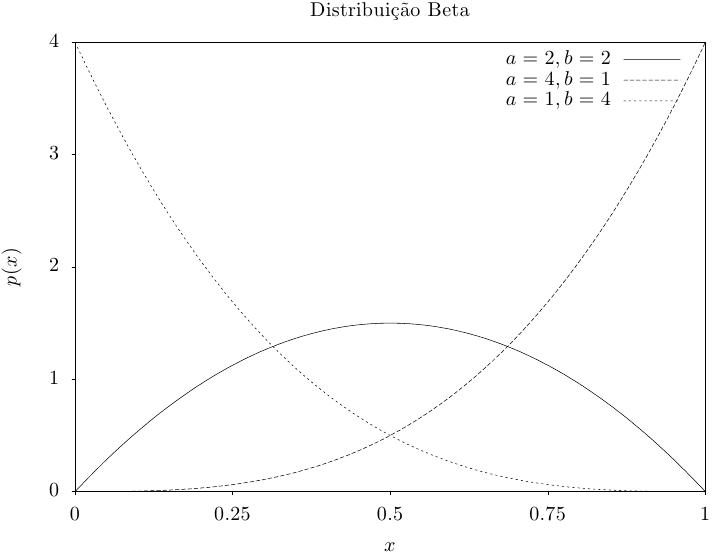
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição beta com parâmetros a e b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição
logística. A função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição logística com parâmetro de ajuste proporcional a, usando a fórmula fornecida acima.
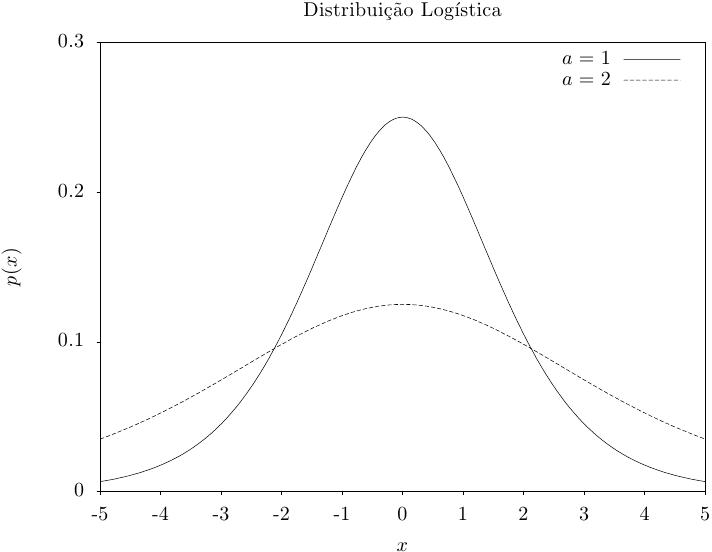
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição logística com parâmetro de ajuste proporcional a.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir de uma distribuição de Pareto de
ordem a. A função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Pareto com expoente a e ajuste proporcional b, usando a fórmula fornecida acima.
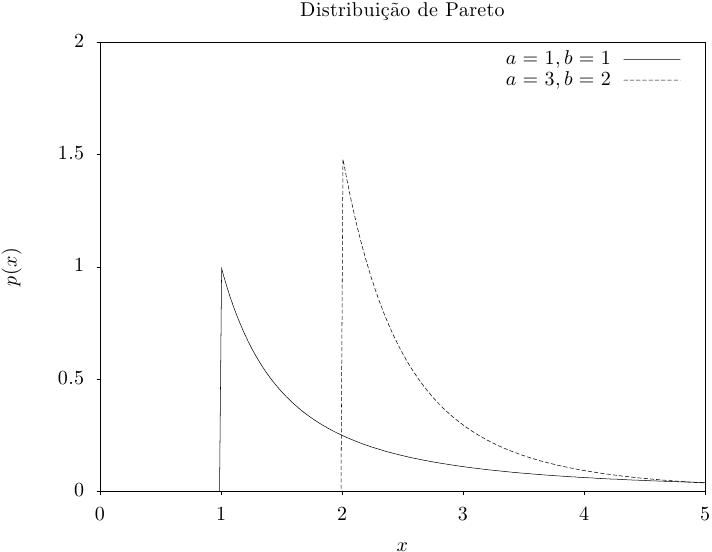
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Pareto com expoente a e ajuste proporcional b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
As distribuições esféricas geram vetores aleatórios, localizados sobre uma superfície esférica. Eles podem ser usados como direções aleatórias, po exemplo nos passos de uma caminhada aleatória.
Essa função retorna um vetor de direção aleatória v = (x,y) em duas dimensões. O vetor é normalizado de forma que |v|^2 = x^2 + y^2 = 1. O caminho óbvio para fazer isso é tomar um número aleatório uniforme entre 0 e 2\pi e pegar x e y como sendo o seno e o cosseno respectivamente. Duas funções trigonométricas podem ter sido dispendiosas nos velhos dias, mas com modernas implementações de hardware, esse é algumas vezes o caminho mais rápido a seguir. Esse é o caso para o Pentium (mas não o caso para Sun Sparcstation). Se pode evitar as avaliações trigonométricas escolhendo x e y no interior de círculo unitário (escolha-os em aleatoriedade a partir do interior do quadrado circunscrito, a seguir rejeite aqueles que estiverem fora do círculo unitário), e conclua dividindo por \sqrt{x^2 + y^2}. Uma aproximação mais inteligente, atribuida a von Neumann (Veja em Knuth, v2, 3a. ed, p140, exercício 23), não precisa nem de trigonometria nem de uma raís quadrada. Nessa aproximação, u e v são escolhidos de forma aleatória a partir do interior de um círculo unitário, e então x=(u^2-v^2)/(u^2+v^2) e y=2uv/(u^2+v^2).
Essa função retorna um vetor de direção aleatório v = (x,y,z) em três dimensões. O vetor é normalizado de forma que |v|^2 = x^2 + y^2 + z^2 = 1. O método usado é devido a Robert E. Knop (CACM 13, 326 (1970)), e explicado em Knuth, v2, 3a. ed, p136. Usa o surpreendente fato de que a distribuição projetada ao longo de qualquer eixo é atualmente uniforme (isso é somente verdadeiro para 3 dimensões).
Essa função retorna um vetor de direção aleatório v = (x_1,x_2,...,x_n) em n dimensões. O vetor é normalizado de forma que |v|^2 = x_1^2 + x_2^2 + ... + x_n^2 = 1. O método usa o fato de que uma distribuição de Gauss com vários conjuntos de variáveis é esfericamente simétrica. Cada componente é gerado para ter uma distribuição de Gauss, e então as componentes são normalizadas. O método é descrito por Knuth, v2, 3a. ed, p135–136, e atribuido a G. W. Brown, Modern Mathematics for the Engineer (1956).
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir de uma distribuição de Weibull. A
função de distribuição é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Weibull com ajuste de proporcionalidade a e expoente b, usando a fórmula fornecida acima.
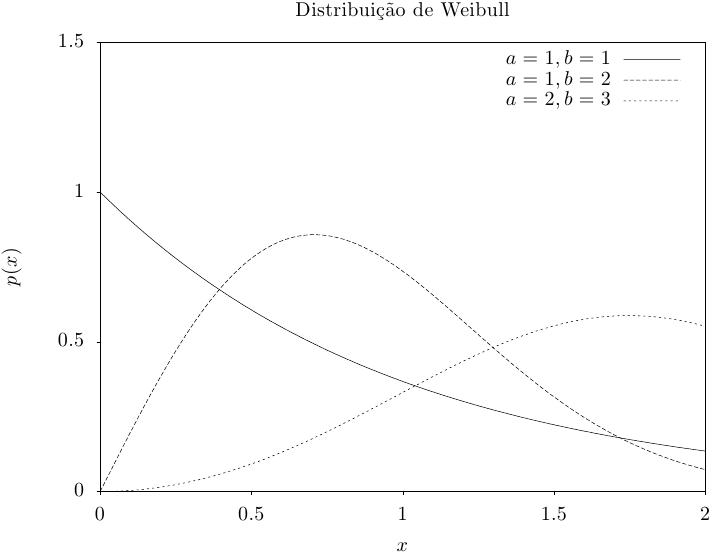
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Weibull com ajuste de proporcionalidade a e expoente b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição de Gumbel
do Tipo-1. A função da distribuição de Gumbel do Tipo-1 é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Gumbel do Tipo-1 com parâmetros a e b, usando a fórmula fornecida acima.
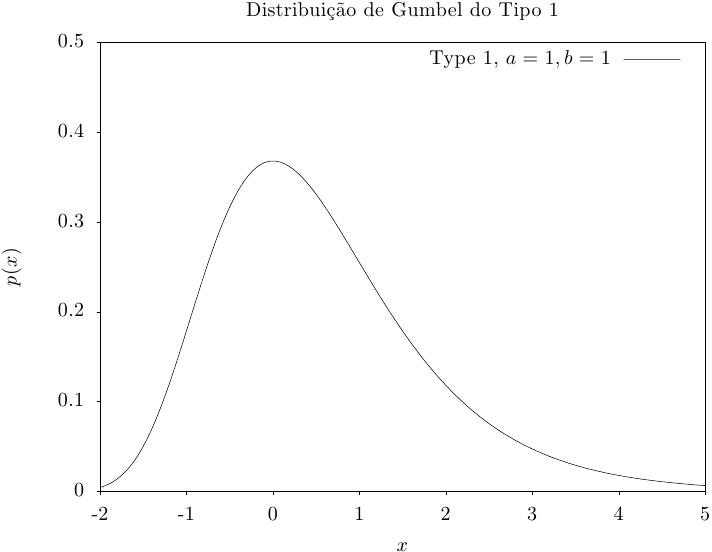
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Gumbel do Tipo-1 com parâmetros a e b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um conjunto de valores aleatórios a partir da distribuição de
Gumbel do Tipo-2. A função da distribuição de Gumbel do Tipo-2 é,
|
Essa função calcula a densidade de probabilidade p(x) em x para uma distribuição de Gumbel do Tipo-2 com parâmetros a e b, usando a fórmula fornecida acima.
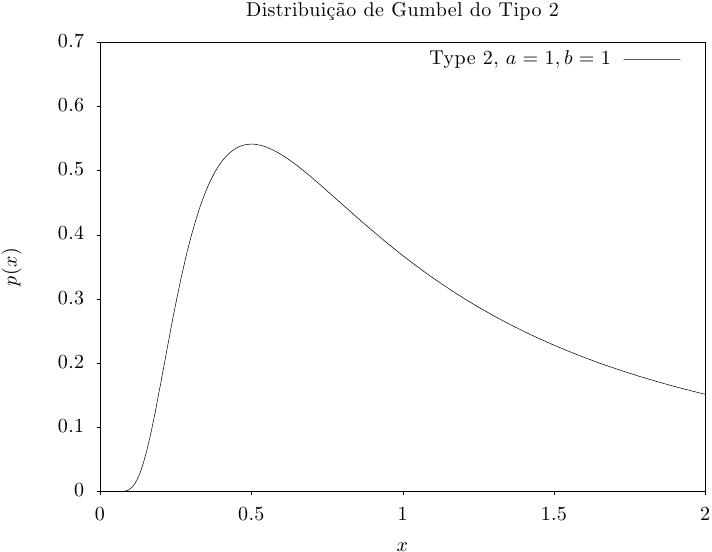
Essas funções calculam as funções de distribuição acumulada P(x), Q(x) e suas inversas para a distribuição de Gumbel do Tipo-2 Gumbel com parâmetros a e b.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um vetor estático de K conjuntos de valores aleatórios a partir de uma distribuição de
Dirichlet de ordem K-1. A função de distribuição é
|
|
O conjunto de valores aleatórios são gerados por amostragem sobre K valores a partir de distribuições gama com parâmetros a=alpha_i, b=1, e renormalizando. Veja A.M. Law, W.D. Kelton, Simulation Modeling and Analysis (1991).
Essa função calcula a densidade de probabilidade p(\theta_1, ... , \theta_K) em theta[K] para uma distribuição de Dirichlet com parâmetros alpha[K], usando a fórmula fornecida acima.
Essa função calcula o logaritmo da densidade de probabilidade p(\theta_1, ... , \theta_K) para uma Dirichlet distribuição com parâmetros alpha[K].
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Dados K eventos discretos com diferentes probabilidade P[k], produz um valor aleatório k consistente com sua probabilidade.
O caminho óbvio para fazer isso é pré-processar a lista de probabilidades
gerando um vetor estático de probabilidade acumulada com K+1 elementos:
|
Mas métodos mais rápidos teem sido desenvolvidos. Novamente, a idéia é pré-processar a lista de probabilidade, e gavar o resultado de slguma forma de tabela de consulta; então as chamadas individuais para um evento discreto aleatório pode ser feita rapidamente. Uma aproximação criada por G. Marsaglia (Generating discrete random variables in a computer, Comm ACM 6, 37–38 (1963)) é muito inteligente, e leitores interessados em exemplos de bom desenho de algoritmo são direcionados para esse curto e bem escrito artigo. Desafortunadamente, para grandes valores de K, a tabela de consulta de Marsaglia pode ser bastante grande.
Uma melhor aproximação é devida a Alastair J. Walker (An efficient method for generating discrete random variables with general distributions, ACM Trans on Mathematical Software 3, 253–256 (1977); veja também Knuth, v2, 3a. ed, p120–121,139). Requer duas tabelas de consulta, uma em ponto flutuante e uma inteira, mas ambas somente de tamanho K. Após pré-processar, os números aleatórios são gerados em tempo O(1), mesmo para grandes valores de K. O pré-processamento sugerido por Walker requer esforço O(K^2), mas que não é atualmente necessário, e a implementação fornecida aqui somente usa esforço O(K). Em geral, mais pré-processamento conduz a geração mais rápida de números aleatórios individuais, mas um diminuto retorno é alcançado no início. Knuth mostra que o pré-processamento ótimo é combinatorialmente difícil para grandes valores de K.
Esse método pode ser usado para aumentar a velocidade de alguns dos geradores de números aleatórios discretos abaixo, tais como a distribuição binomial. Usar esse método para alguma coisa como a Distribuição de Poisson, uma modificação pode ter que ser feita, uma vez que esse método somente pega um finito conjunto de K saídas.
Essa função retorna um apontador para uma estrutura que contém a tabela
de consulta para o gerador de números aleatórios discreto. O vetor estático P[] contém
as probabilidades dos eventos discretos; esses elementos de vetor estático devem todos serem
positivos, mas eles não precisam serem acrescentados a um (de forma que você pode pensar neles mais
geralmente como “pesos”)—o pré-processador irá normalizá-los apropriadamente.
Esse valor de retorno é usado
como um argumento para a função gsl_ran_discrete abaixo.
Após o pré-processador, acima, ter sido chamado, você usa essa função para pegar os números aleatórios discretos.
Retorna a probabilidade P[k] de observar a variável k. Uma vez que P[k] não é armazenado como parte da tabela de consulta, deve ser recalculado; esse recálculo toma O(K), de forma que se K for muito grande e você garante que o vetor estático original P[k] usado para criar a tabela de consulta, então você deve apenas manter esse vetor estático original P[k] por perto.
Desaloca a tabela de consulta apontada por g.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um inteiro aleatório a partir de uma distribuição de Poisson
com média mu. A distribuição de probabilidade para um conjunto de valores de Poisson é,
|
Essa função calcula a probabilidade p(k) de obter k a partir de uma distribuição de Poisson com média mu, usando a fórmula fornecida acima.
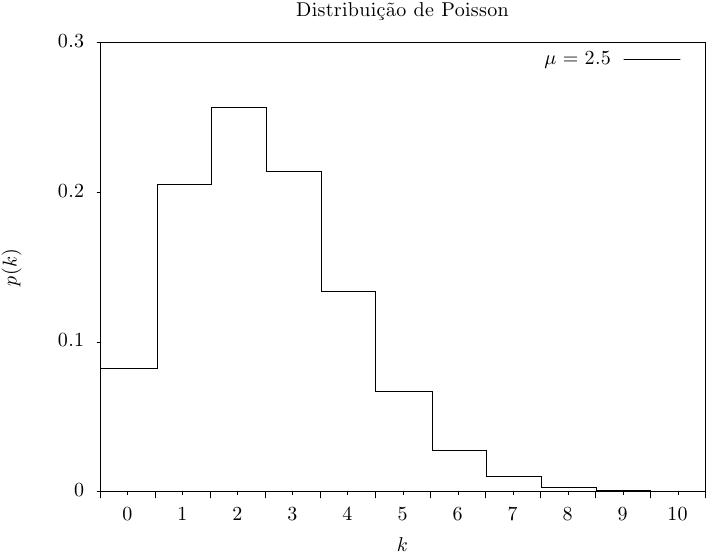
Essas funções calculam as funções de distribuição acumulada P(k), Q(k) para a distribuição de Poisson com parâmetro mu.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna ou 0 ou 1, o resultado de um teste de Bernoulli
com probabilidade p. A distribuição de probabilidade para um teste de
Bernoulli é,
|
Essa função calcula a probabilidade p(k) de obter k a partir de uma distribuição de Bernoulli com parâmetro de probabilidade p, usando a fórmula fornecida acima.
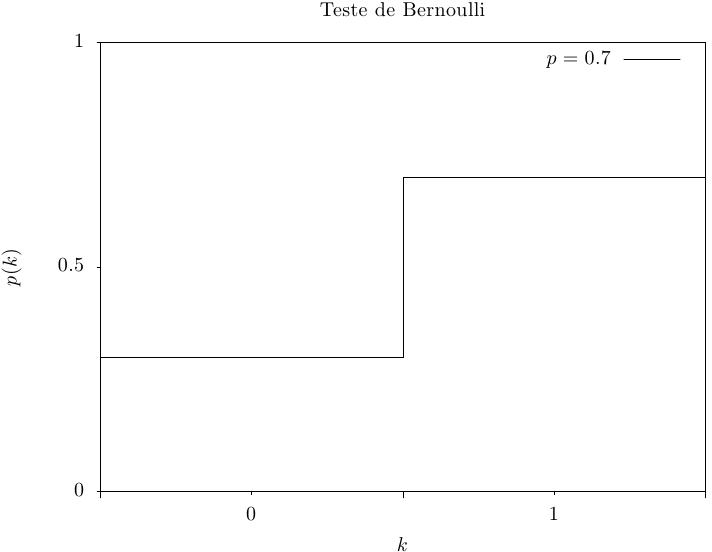
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um inteiro aleatório a partir da distribuição binomial,
o número de sucessos em n testes independentes com probabilidade
p. A distribuição de probabilidade para um conjunto de valores binomiais é,
|
Essa função calcula a probabilidade p(k) de obter k a partir de uma distribuição binomial com parâmetros p e n, usando a fórmula fornecida acima.
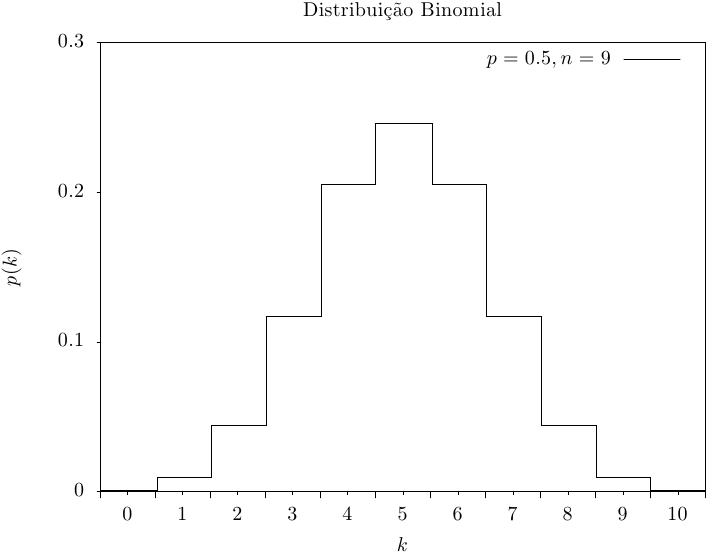
Essas funções calculam as funções de distribuição acumulada P(k), Q(k) para a distribuição binomial com parâmetros p e n.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função calcula uma aostra aleatória n[] a partir da distribuição
multinomial formada por N testes a partir de um distribuição básica
p[K]. A função de distribuição para n[] é,
|
Conjunto de valores aleatórios são gerados usando o método condicional binomial (veja C.S. Davis, The computer generation of multinomial random variates, Comp. Stat. Data Anal. 16 (1993) 205–217 para detalhes).
Essa função calcula a probabilidade P(n_1, n_2, ..., n_K) de amostragem n[K] a partir de uma distribuição multinomial com parâmetros p[K], usando a fórmula fornecida acima.
Essa função retorna o logaritmo da probabilidade para a distribuição multinomial P(n_1, n_2, ..., n_K) com parâmetros p[K].
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um inteiro aleatório a partir da distribuição binomial
negativa, o número de falhas ocorridas antes de n sucessos
em testes independentes com probabilidade p de sucessos. A
distribuição de probabilidade para conjunto de valores binomiais negativos é,
|
Essa função calcula a probabilidade p(k) de obter k a partir de uma distribuição binomial negativa com parâmetros p e n, usando a fórmula fornecida acima.
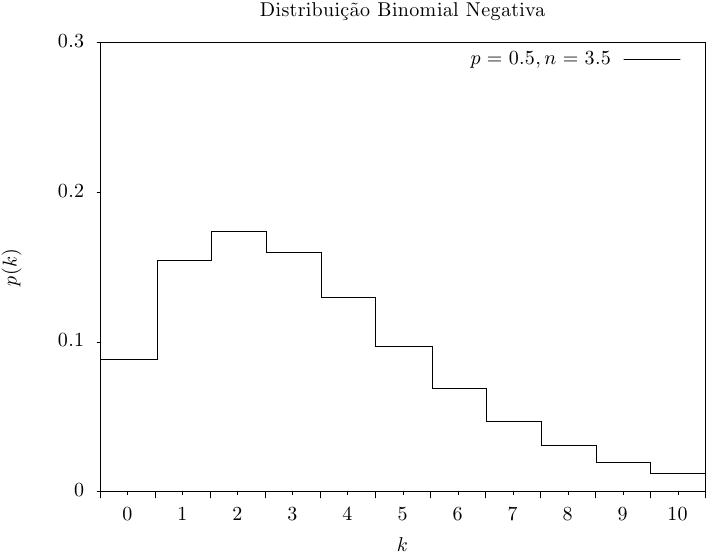
Essas funções calculam as funções de distribuição acumulada P(k), Q(k) para a distribuição binomial negativa com parameters p e n.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um inteiro aleatório a partir da distribuição de Pascal. A
distribuição de Pascal é simplesmente uma distribuição binomial negativa com um
valor inteiro de n.
|
Essa função calcula a probabilidade p(k) de obter k a partir de uma distribuição de Pascal com parâmetros p e n, usando a fórmula fornecida acima.
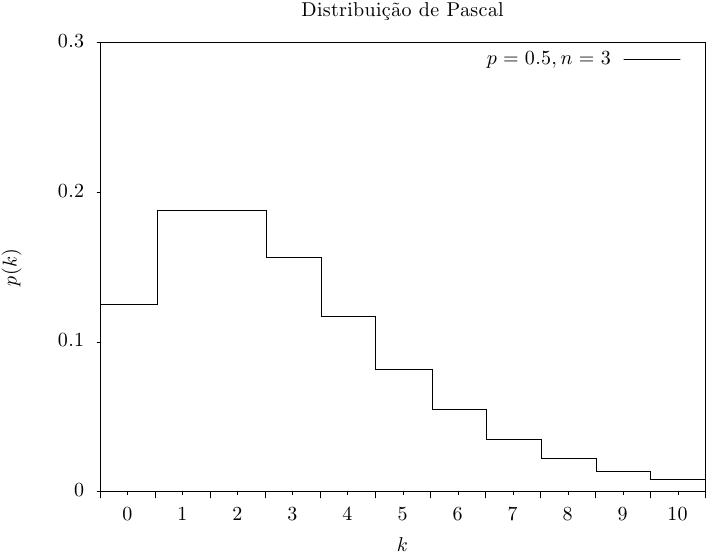
Essas funções calculam as funções de distribuição acumulada P(k), Q(k) para a distribuição de Pascal com parâmetros p e n.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um inteiro aleatório a partir da distribuição geométrica,
o número de testes independentes com probabilidade p até que ocorra o
primeiro sucesso. A distribuição de probabilidade para o conjunto de valores geométricos
é,
|
Essa função calcula a probabilidade p(k) de obter k a partir de uma distribuição geométrica com parâmetro de probabilidade p, usando a fórmula fornecida acima.
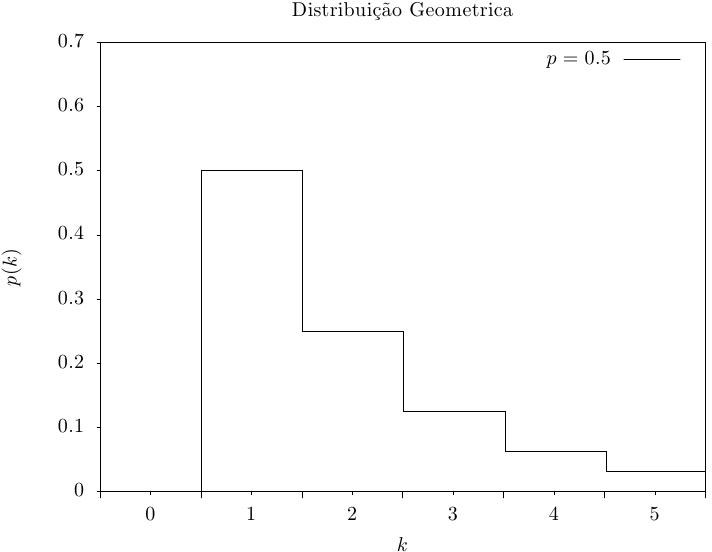
Essas funções calculam as funções de distribuição acumulada P(k), Q(k) para a distribuição geométrica com parâmetro p.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função retorna um inteiro aleatório a partir da distribuição
hipergeométrica. A distribuição de probabilidade para conjunto de valores aleatórios
hipergeométricos é,
|
Se uma população contém n_1 elementos do “tipo 1” e n_2 elementos do “tipo 2” então a distribuição hipergeométrica fornece a probabilidade de obter k elementos do “tipo 1” em t amostras a partir da população sem substituição.
Essa função calcula a probabilidade p(k) de obter k a partir de uma distribuição hipergeométrica com parâmetros n1, n2, t, usando a fórmula fornecida acima.
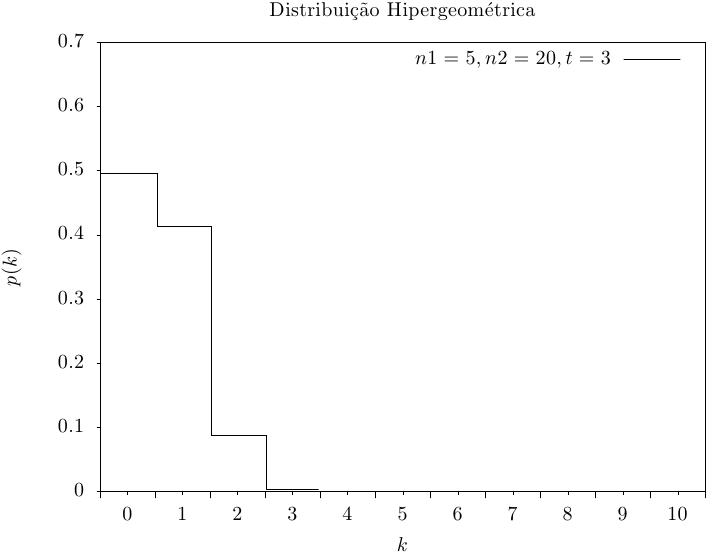
Essas funções calculam as funções de distribuição acumulada P(k), Q(k) para a distribuição hipergeométrica com parâmetros n1, n2 e t.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
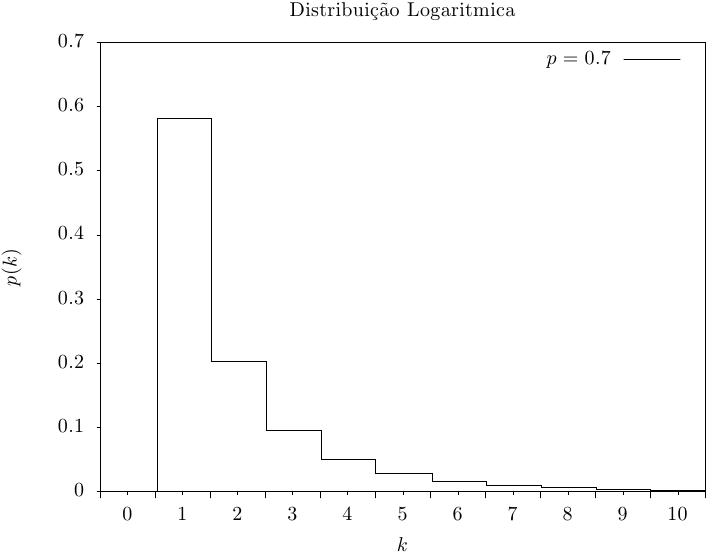
Essa função retorna um inteiro aleatório a partir da distribuição
logarítmica. A distribuição de probabilidade para conjuntos de valores aleatórios logarítmicos
é,
|
Essa função calcula a probabilidade p(k) de obter k from a distribuição logarítmica com parâmetro de probabilidade p, usando a fórmula fornecida acima.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
As seguintes funções permitem o embaralhamento e amostragem de um conjunto de objetos. Os algoritmos com certeza usam um gerador de números aleatórios como uma fonte de aleatoriedade e um gerador de baixa qualidade pode levar a correlações na saída. Em particular é importante evitar geradores com períodos curtos. Para mais informação veja, v2, 3a. ed, Seção 3.4.2, “Random Sampling and Shuffling”.
Essa função embaralha aleatoriamente a ordem de n objetos, cada um de tamanho size, armazenados no vetor estático base[0..n-1]. A saída do gerador de números aleatórios r é usada para produzir a permutação. O algoritmo gera todas as possíveis n! permutações com igual probabilidade, assumindo uma fonte perfeita de números aleatórios.
O seguinte código mostra como embaralhar os números de 0 a 51,
int a[52];
for (i = 0; i < 52; i++)
{
a[i] = i;
}
gsl_ran_shuffle (r, a, 52, sizeof (int));
Essa função preenche o vetor estático dest[k] com k objetos tomados aleatoriamente a partir de n elementos do vetor estático src[0..n-1]. Os objetos são cada um de tamanho size. A saída do gerador de números aleatórios r é usada para fazer a seleção. O algoritmo garante que todas as possíveis amostras são igualmente prováveis, assumindo uma perfeita fonte de aleatoriedade.
Os objetos são retirados para fazerem parte da amostra sem substituição, dessa forma cada objeto pode
somente aparecer uma vez em dest[k]. É obrigatório que k seja menor
que ou igual a n. Os objetos em dest irão estar na
mesma ordem relativa daqueles em src. Você irá precisar chamar
gsl_ran_shuffle(r, dest, n, size) se você desejar aleatorizar a
ordem.
O seguinte código mostra como selecionar uma amostr aleatória de três números únicos a aprtir do conjunto de 0 a 99,
double a[3], b[100];
for (i = 0; i < 100; i++)
{
b[i] = (double) i;
}
gsl_ran_choose (r, a, 3, b, 100, sizeof (double));
Essa função é como a gsl_ran_choose mas faz amostras de k itens
a partir do vetor estático original de n itens src com substituição, de forma que
o mesmo objeto pode aparecer mais que uma vez na sequência de saída
dest. Não existe obrigatoriedade que k seja menor que n
nesse caso.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O seguinte programa demonstra o uso de um gerador de números aleatórios para produzir um conjunto de números a partir de uma distribuição. Exibe 10 amostras a partir da distribuição de Poisson com média 3.
#include <stdio.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
int
main (void)
{
const gsl_rng_type * T;
gsl_rng * r;
int i, n = 10;
double mu = 3.0;
/* create a generator chosen by the
environment variable GSL_RNG_TYPE */
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc (T);
/* print n random variates chosen from
the poisson distribution with mean
parameter mu */
for (i = 0; i < n; i++)
{
unsigned int k = gsl_ran_poisson (r, mu);
printf (" %u", k);
}
printf ("\n");
gsl_rng_free (r);
return 0;
}
Se a biblioteca e arquivos de cabeçalho são instalados em ‘/usr/local’ (a localização padrão) então o programa pode ser compilado com essas opções,
$ gcc -Wall demo.c -lgsl -lgslcblas -lm
Aqui está a saída do programa,
$ ./a.out2 5 5 2 1 0 3 4 1 1
O conjunto de valores depende da semente usada pelo gerador. A semente para o
tipo de gerador padrão gsl_rng_default pode ser mudada com a
variável de ambiente GSL_RNG_SEED para produzir um fluxo diferente
de conjunto de valores,
$ GSL_RNG_SEED=123 ./a.outGSL_RNG_SEED=123 4 5 6 3 3 1 4 2 5 5
O seguinte programa gera uma caminhada aleatória em duas dimensões.
#include <stdio.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
int
main (void)
{
int i;
double x = 0, y = 0, dx, dy;
const gsl_rng_type * T;
gsl_rng * r;
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc (T);
printf ("%g %g\n", x, y);
for (i = 0; i < 10; i++)
{
gsl_ran_dir_2d (r, &dx, &dy);
x += dx; y += dy;
printf ("%g %g\n", x, y);
}
gsl_rng_free (r);
return 0;
}
Aqui está uma saída do programa, quatro caminhadas aleatórias de 10 passos a partir da orígem,
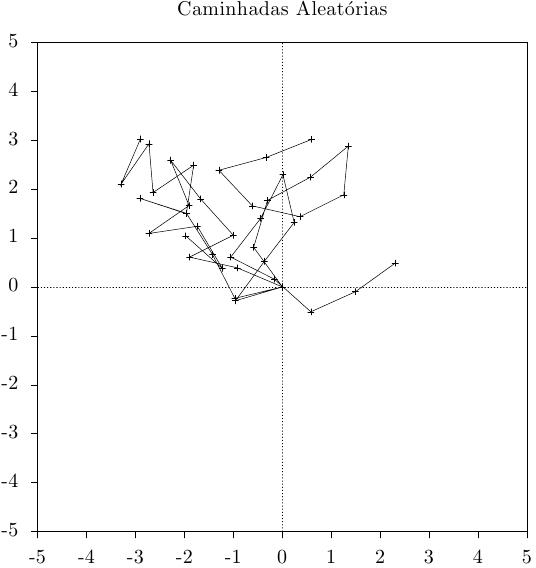
O seguinte programa calcula as funções de distribuição acumuladas alta e baixa para a distribuição normal padrão em x=2.
#include <stdio.h>
#include <gsl/gsl_cdf.h>
int
main (void)
{
double P, Q;
double x = 2.0;
P = gsl_cdf_ugaussian_P (x);
printf ("prob(x < %f) = %f\n", x, P);
Q = gsl_cdf_ugaussian_Q (x);
printf ("prob(x > %f) = %f\n", x, Q);
x = gsl_cdf_ugaussian_Pinv (P);
printf ("Pinv(%f) = %f\n", P, x);
x = gsl_cdf_ugaussian_Qinv (Q);
printf ("Qinv(%f) = %f\n", Q, x);
return 0;
}
Aqui está a saída do programa,
prob(x < 2.000000) = 0.977250 prob(x > 2.000000) = 0.022750 Pinv(0.977250) = 2.000000 Qinv(0.022750) = 2.000000
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Para uma abrangência enciclopédica dos leitores do assunto é aconselhado consultar o livro Non-Uniform Random Variate Generation de Luc Devroye. O livro abrange toda distribuição imaginável e fornece centenas de algoritmos.
O assunto de geração de conjuntos de valores aleatórios é também revisado por Knuth, que descreve algoritmos para todas as principais distribuiçẽos.
O Grupo de Dados de Particulas fornece uma curta revisão de técnicas para gerar distribuiçẽos de números aleatórios na seção “Monte Carlo” de seu Annual Review of Particle Physics.
O Review of Particle Physics está disponível online nos formatos postscript e pdf.
Uma visão geral de métodos usados para calcular funções de distribuição acumulada pode ser encontrado em Statistical Computing por W.J. Kennedy e J.E. Gentle. Outra referência geral é Elements of Statistical Computing por R.A. Thisted.
As funções de distribuições acumuladas para a distribuição de Gauss são baseados nos seguintes artigos,
| [ << ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.