29 Aproximações de Chebychev

Esse capítulo descreve rotinas para calcular aproximações de Chebyshev para funções com uma variável dependente. Uma aproximação de Chebyshev é uma truncagem das séries f(x) = \sum c_n T_n(x), onde os polinômios de Chebyshev T_n(x) = \cos(n \arccos x) fornecem uma base ortogonal de polinômios do intervalo [-1,1] com a função peso 1 / \sqrt{1-x^2}. Os primeiros poucos polinômios de Chebyshev são, T_0(x) = 1, T_1(x) = x, T_2(x) = 2 x^2 - 1. Para informação adicional veja Abramowitz & Stegun, Capítulo 22.

As funções descritas nesse capítulo são declaradas no arquivo de cabeçalho ‘gsl_chebyshev.h’.

29.1 Definições

Uma série de Chebyshev é armazenada usando a seguinte estrutura,

typedef struct
{
  double * c;   /* coefficients  c[0] .. c[order] */
  int order;    /* order of expansion             */
  double a;     /* lower interval point           */
  double b;     /* upper interval point           */
  ...
} gsl_cheb_series

A aproximação é feita sobre o intervalo [a,b] usando order+1 termos, incluindo o coeficiente c[0]. As séries são calculadas usando a seguinte convenção, que é necessária quando acessamos os coeficientes diretamente.

29.2 Criação e Cálculo de Séries de Chebychev

Function: gsl_cheb_series * gsl_cheb_alloc (const size_t n): Essa função aloca espaço para uma série de Chebyshev de ordem n e retorna um apontador para uma nova estrutura gsl_cheb_series.

Function: void gsl_cheb_free (gsl_cheb_series * cs): Essa função libera uma série de Chebyshev cs que foi alocada anteriormente.

Function: int gsl_cheb_init (gsl_cheb_series * cs, const gsl_function * f, const double a, const double b): Essa função calcula a aproximação de Chebyshev cs para a função f sobre o intervalo (a,b) para a ordem especificada anteriormente. O cálculo da aproximação de Chebyshev é um processo O(n^2) (53), e requer n avaliações de função.

29.3 Funções Auxiliares

As seguintes funções fornecem informação sobre uma série de Chebyshev que já existe.

Function: size_t gsl_cheb_order (const gsl_cheb_series * cs): Essa função retorna a ordem da série de Chebyshev cs.

Function: size_t gsl_cheb_size (const gsl_cheb_series * cs)
Function: double * gsl_cheb_coeffs (const gsl_cheb_series * cs): Essas funções retornam o tamanho do vetor estático de coeficiente de Chebyshev c[] e um apontador para sua primeira localização na memória para as séries de Chebyshev cs.

29.4 Avaliação de Séries de chebychev

Function: double gsl_cheb_eval (const gsl_cheb_series * cs, double x): Essa função avalia a série de Chebyshev cs em um dado ponto x.

Function: int gsl_cheb_eval_err (const gsl_cheb_series * cs, const double x, double * result, double * abserr): Essa função calcula a série de Chebyshev cs em um dado ponto x, estimando ambos o resultado result das séries e seu erro absoluto abserr. O erro estimado é feito a partir do primeiro termo negligenciado nas séries.

Function: double gsl_cheb_eval_n (const gsl_cheb_series * cs, size_t order, double x): Essa função avalia a série de Chebyshev cs em um dado ponto x, para (no máximo) a dada ordem order.

Function: int gsl_cheb_eval_n_err (const gsl_cheb_series * cs, const size_t order, const double x, double * result, double * abserr): Essa função avalia uma série de Chebyshev cs em um dado ponto x, estimando ambos o resultado result da série e seu erro absoluto abserr, para (no máximo) a ordem dada order. O erro estimado é feito a partir do primeiro termo negligenciado na série.

29.5 Integrais e Derivadas

As seguintes funções permitem a uma série de Chebyshev ser diferenciada ou integrada, produzindo uma nóva série de Chebyshev. Note que o erro estimado produzido pela avaliação da série derivada irá ser estimado para baixo devido à contribuição dos termos de alta ordem sendo abandonados.

Function: int gsl_cheb_calc_deriv (gsl_cheb_series * deriv, const gsl_cheb_series * cs): Essa função calcula a derivada da série cs, armazenando os coeficientes da derivada em deriv alocada anteriormente. As duas séries cs e deriv devem ter sido alocadas com a mesma ordem.

Function: int gsl_cheb_calc_integ (gsl_cheb_series * integ, const gsl_cheb_series * cs): Essa função calcula a integral da série cs, armazenando os coeficientes da integral em integ alocada anteriormente. As duas séries cs e integ devem ter sido alocadas com a mesma ordem. O limite inferior da integração é tomado para ser o início do intervalo a.

29.6 Exemplos

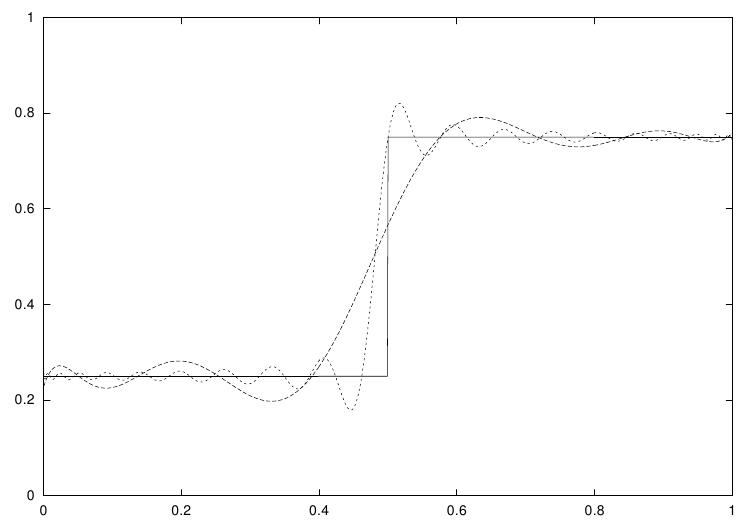
O seguinte programa exemplo calcula aproximações de Chebyshev para uma função degrau. Essa é uma aproximação extremamente difícil de fazer, devido a descontinuidades, e foi escolhida como um exemplo onde o erro de aproximação é visível. Para funções planas a aproximação de Chebyshev converge extremamente rápido e erros podem não serem visíveis.

#include <stdio.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_chebyshev.h>

double
f (double x, void *p)
{
  if (x < 0.5)
    return 0.25;
  else
    return 0.75;
}

int
main (void)
{
  int i, n = 10000; 

  gsl_cheb_series *cs = gsl_cheb_alloc (40);

  gsl_function F;

  F.function = f;
  F.params = 0;

  gsl_cheb_init (cs, &F, 0.0, 1.0);

  for (i = 0; i < n; i++)
    {
      double x = i / (double)n;
      double r10 = gsl_cheb_eval_n (cs, 10, x);
      double r40 = gsl_cheb_eval (cs, x);
      printf ("%g %g %g %g\n", 
              x, GSL_FN_EVAL (&F, x), r10, r40);
    }

  gsl_cheb_free (cs);

  return 0;
}

A saída do programa fornece a função original, uma aproximação de décima ordem e uma aproximação de quadragésima ordem, todas com amostras retiradas em intervalos de 0.001 em x.

29.7 Referências e Leituras Adicionais

O seguinte artigo descreve o uso de séries de Chebyshev,

R. Broucke, “Ten Subroutines for the Manipulation of Chebyshev Series [C1] (Algorithm 446)”. Communications of the ACM 16(4), 254–256 (1973)

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.