31 Transformadas Wavelet

Esse capítulo descreve funções para executar Transformadas Wavelet Discretas (DWTs (55)). A biblioteca inclui wavelets para dados reais em ambas uma e duas dimensões. As funções wavelet são declaradas nos arquivos de cabeçalho ‘gsl_wavelet.h’ e ‘gsl_wavelet2d.h’.

31.1 Definições

A transformada wavelet contínua e sua inversa são definidas pelas relações,

w(s, τ) =

⌠
⌡

∞

−∞

f(t) * ψ^*_s,τ(t) dt

f(t) =

⌠
⌡

∞

0

⌠
⌡

∞

−∞

w(s, τ) * ψ_s,τ(t) dτ

onde as funções base \psi_{s,\tau} são obtidas pelo ajuste proporcional e translação a partir de uma função simples, referida como a mother wavelet - wavelet mãe.

A versão discreta da transformada wavelet atua sobre amostras equitativamente espaçadas, com passos de translações e ajustes proporcionais (s, \tau). Dos eixos de frequência e tempo são retiradas amostras diádicamente sobre ajustes proporcionais de 2^j através de um parâmetro de nível j. A família resultante de funções {\psi_{j,n}} constitue uma base ortonormal para sinais de quadrados integráveis.

A transformada wavelet discreta é um algoritmo O(N), e é também referenciado como transformada wavelet rápida.

31.2 Inicialização

A estrutura gsl_wavelet contém os coeficientes de filtro definindo a wavelet e quaisquer parâmetros de deslocamento associado.

Function: gsl_wavelet * gsl_wavelet_alloc (const gsl_wavelet_type * T, size_t k): Essa função aloca e inicializa um objeto wavelet do tipo T. O parâmetro k seleciona o membro específico da família de wavelet. Um apontador nulo é retornado se não tiver memória suficiente disponível ou se um membro não suportado for selecionado.

Os seguintes tipos de wavelet são implementados:

Wavelet: gsl_wavelet_daubechies
Wavelet: gsl_wavelet_daubechies_centered: Essa é a família de wavelets de Daubechies (56) de fase máxima com k/2 momentos tendendo para zero. As wavelets implementadas são k=4, 6, …, 20, com k sendo um número par.

Wavelet: gsl_wavelet_haar
Wavelet: gsl_wavelet_haar_centered: Essa é a wavelet de Haar (57). A única escolha válida de k para a wavelet de Haar é k=2.

Wavelet: gsl_wavelet_bspline
Wavelet: gsl_wavelet_bspline_centered: Essa é a família de wavelet B-spline biortogonal de ordem (i,j). Os valores implementados de k = 100*i + j são 103, 105, 202, 204, 206, 208, 301, 303, 305 307, 309.

As formas centradas de wavelets alinham com os coeficientes de várias sub-bandas sobre arestas. Dessa forma a visualização resultante dos coeficientes da transformada wavelet no plano de fase é fácil para entender.

Function: const char * gsl_wavelet_name (const gsl_wavelet * w): Essa função retorna um apontador para o nome da família de wavelet para w.

Function: void gsl_wavelet_free (gsl_wavelet * w): Essa função libera o objeto wavelet w.

A estrutura gsl_wavelet_workspace contém espaço de rascunho do mesmo tamanho que os dados de entrada e é usado para manter resultados intermediários durante a tranformação.

Function: gsl_wavelet_workspace * gsl_wavelet_workspace_alloc (size_t n): Essa função aloca um espaço de trabalho para a transformada wavelet discreta. Para executar uma transformada unidimensional sobre n elementos, um espaço de trabalho de tamanho n deve ser fornecido. Para transformadas bidimensionais de matrizes n-por-n é suficiente alocar um espaço de trabalho de tamanho n, uma vez que a transformada opera sobre linhas individuais e colunas individuais. Um apontador nulo é retornado se não houver memória suficiente disponível.

Function: void gsl_wavelet_workspace_free (gsl_wavelet_workspace * work): Essa função libera o espaço de trabalho alocado work.

31.3 Funções de Transformada

Essa seção descreve as funções atuais executando a transformada wavelet discreta. Note que as transformadas usam condições associadas periódicas. Se o sinal não for periódico no comprimento da amostra então coeficientes espúrios irão aparecer no início e no fim de cada nível da transformada.

31.3.1 Transformadas wavelets em uma dimensão

Function: int gsl_wavelet_transform (const gsl_wavelet * w, double * data, size_t stride, size_t n, gsl_wavelet_direction dir, gsl_wavelet_workspace * work)

Function: int gsl_wavelet_transform_forward (const gsl_wavelet * w, double * data, size_t stride, size_t n, gsl_wavelet_workspace * work)

Function: int gsl_wavelet_transform_inverse (const gsl_wavelet * w, double * data, size_t stride, size_t n, gsl_wavelet_workspace * work)

Essas funções calculam transformadas wavelet discretas localmente pela direita e transformadas wavelet discretas localmente inversa ambas de comprimento n com salto stride sobre o vetor estático data. O comprimento da transformada n é restrito a potências de base dois. Para a versão transform da função o argumento dir pode ser ou forward (+1) (58) ou backward (59) (-1). Um espaço de trabalho work de comprimento n deve ser fornecido.

Para a transformada pela direita, os elementos do vetor estático original são substituídos pela transformada wavelet discreta f_i -> w_{j,k} em um esquema de armazenamento triangular empacotado, onde j é o índice do nível j = 0 ... J-1 e k é o índice do coeficiente dentro de cada nível, k = 0 ... (2^j)-1. O número total de níveis é J = \log_2(n). Os dados de saída possuem a seguinte forma,

(s_−1,0, d_0,0, d_1,0, d_1,1, d_2,0,…, d_j,k,…, d_{J−1,2^J−1 − 1})

onde o primeiro elemento é o coeficiente de suavização s_{-1,0}, seguindo pelos coeficientes de detalhamento d_{j,k} para cada nível j. A transformada pela esquerda inverte esses coeficientes para obter os dados originais.

Essas funções retornam uma situação atual de GSL_SUCCESS em caso de terem completado a tarefa com sucesso. A situação atual de GSL_EINVAL é retornada se n não for uma potência inteira de base dois ou se um espaço de trabalho insuficiente for fornecido.

31.3.2 Transformadas wavelet em duas dimensões

A biblioteca fornece funções para executar transformadas wavelets discretas bidimensionais sobre matrizes quadradas. As dimensões da matriz devem ser uma potência inteira de base dois. Existe duas possíveis ordenações de linhas e colunas na transformada wavelet bidimensional, referenciadas como forma “padrão” e forma “não padrão”.

A transformada “padrão” executa uma completa transformada wavelet discreta sobre as linhas da matriz, seguida por uma transformada wavelet discreta completa separada sobre as colunas da resultante matriz linha transformada. Esse procedimento usa a mesma ordenação usada na transformada de Fourier bidimensional.

A transformada “não padrão” é executada em etapas intercaladas sobre as linhas e as colunas da matriz para cada nível da transformada. O primeiro nível da transformada é aplicado às linhas da matriz e em seguida colunas da matriz. Esse procedimento é então repetido ao longo de todas as linhas e colunas dos dados para os níveis subsequentes da transformada, até que a transformada wavelet seja completada em sua totalidade. A forma não padrão da transformada wavelet discreta é tipicamente usada em análise de imagem.

As funções descritas nessa seção são declaradas no arquivo de cabeçalho ‘gsl_wavelet2d.h’.

Function: int gsl_wavelet2d_transform (const gsl_wavelet * w, double * data, size_t tda, size_t size1, size_t size2, gsl_wavelet_direction dir, gsl_wavelet_workspace * work)

Function: int gsl_wavelet2d_transform_forward (const gsl_wavelet * w, double * data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace * work)

Function: int gsl_wavelet2d_transform_inverse (const gsl_wavelet * w, double * data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace * work)

Essas funções calculam as transformadas wavelet discretas pela direita e inversa localmente bidimensional na forma padrão sobre o vetor estático data armazenado na forma linha principal com dimensões size1 e size2 e comprimento físico de linha tda. As dimensões devem se iguais (matriz quadrada) e são restritas a potências de base dois. Para a versão transform da função o argumento dir pode ser ou forward (+1)(60) ou backward (-1)(61). Um espaço de trabalho work de tamanho apropriado deve ser fornecido. Na saída, os elementos apropriados da vetor estático data são substituídos por sua transformada wavelet bidimensional.

A função retorna uma situação atual de GSL_SUCCESS em caso de terem completado a tarefa com sucesso. GSL_EINVAL é retornado se size1 e size2 não forem iguais e expoentes inteiros de 2, ou se for fornecido espaço de trabalho insuficiente.

Function: int gsl_wavelet2d_transform_matrix (const gsl_wavelet * w, gsl_matrix * m, gsl_wavelet_direction dir, gsl_wavelet_workspace * work)
Function: int gsl_wavelet2d_transform_matrix_forward (const gsl_wavelet * w, gsl_matrix * m, gsl_wavelet_workspace * work)
Function: int gsl_wavelet2d_transform_matrix_inverse (const gsl_wavelet * w, gsl_matrix * m, gsl_wavelet_workspace * work): Essas funções calculam a transformada wavelet localmente bidimensional sobre uma matriz a.

Function: int gsl_wavelet2d_nstransform (const gsl_wavelet * w, double * data, size_t tda, size_t size1, size_t size2, gsl_wavelet_direction dir, gsl_wavelet_workspace * work)
Function: int gsl_wavelet2d_nstransform_forward (const gsl_wavelet * w, double * data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace * work)
Function: int gsl_wavelet2d_nstransform_inverse (const gsl_wavelet * w, double * data, size_t tda, size_t size1, size_t size2, gsl_wavelet_workspace * work): Essas funções calculam a transformada wavelet bidimensional em sua forma não padrão.

Function: int gsl_wavelet2d_nstransform_matrix (const gsl_wavelet * w, gsl_matrix * m, gsl_wavelet_direction dir, gsl_wavelet_workspace * work)
Function: int gsl_wavelet2d_nstransform_matrix_forward (const gsl_wavelet * w, gsl_matrix * m, gsl_wavelet_workspace * work)
Function: int gsl_wavelet2d_nstransform_matrix_inverse (const gsl_wavelet * w, gsl_matrix * m, gsl_wavelet_workspace * work): Essas funções calculam a forma não padrão da transformada wavelet localmente bidimensional sobre uma matriz a.

31.4 Exemplos

O seguinte programa demonstra o uso das funções de transformada wavelet unidimensionais. Calculam uma aproximação para um sinal entrada (de comprimento 256) usando as 20 maiores componentes da transformada wavelet, enquanto ajusta as outras para zero.

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_sort.h>
#include <gsl/gsl_wavelet.h>

int
main (int argc, char **argv)
{
  int i, n = 256, nc = 20;
  double *data = malloc (n * sizeof (double));
  double *abscoeff = malloc (n * sizeof (double));
  size_t *p = malloc (n * sizeof (size_t));

  FILE * f;
  gsl_wavelet *w;
  gsl_wavelet_workspace *work;

  w = gsl_wavelet_alloc (gsl_wavelet_daubechies, 4);
  work = gsl_wavelet_workspace_alloc (n);

  f = fopen (argv[1], "r");
  for (i = 0; i < n; i++)
    {
      fscanf (f, "%lg", &data[i]);
    }
  fclose (f);

  gsl_wavelet_transform_forward (w, data, 1, n, work);

  for (i = 0; i < n; i++)
    {
      abscoeff[i] = fabs (data[i]);
    }
  
  gsl_sort_index (p, abscoeff, 1, n);
  
  for (i = 0; (i + nc) < n; i++)
    data[p[i]] = 0;
  
  gsl_wavelet_transform_inverse (w, data, 1, n, work);
  
  for (i = 0; i < n; i++)
    {
      printf ("%g\n", data[i]);
    }
  
  gsl_wavelet_free (w);
  gsl_wavelet_workspace_free (work);

  free (data);
  free (abscoeff);
  free (p);
  return 0;
}

A saída pode ser usada com o programa graph contido no pacote GNU plotutils,

$ ./a.out ecg.dat > dwt.dat
$ graph -T ps -x 0 256 32 -h 0.3 -a dwt.dat > dwt.ps

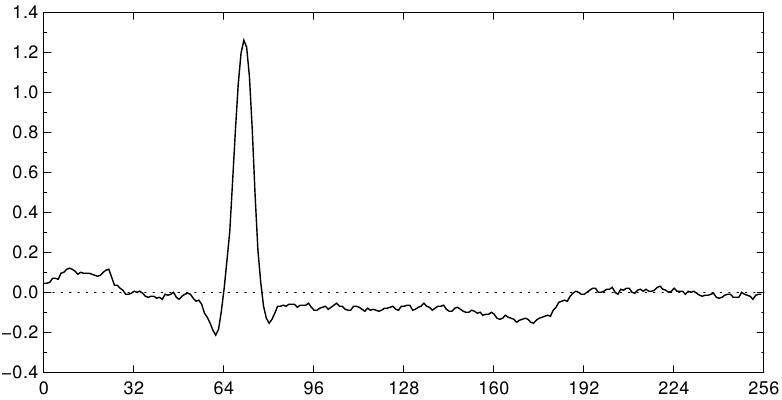
Os gráficos abaixo mostram uma versão original e uma versão comprimida de uma amostra de uma gravação de ECG (62) da MIT-BIH Arrhythmia Database, integrante do arquivo PhysioNet de domínio público do conjunto de dados médicos.

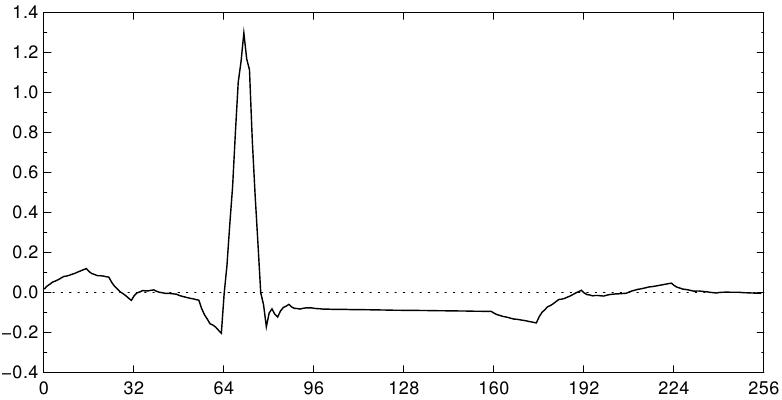
Sinais de ECG original (superior) e wavelet comprimida (inferior), usando as 20 componentes maiores da transformada wavelet discreta de Daubechies(4).

31.5 Referências e Leituras Adicionais

O pano de fundo matemático para transformadas wavelet é abrangido nas anotações originais de Daubechies,

Ingrid Daubechies. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics (1992), SIAM, ISBN 0898712742.

Uma introdução fácil de ler para o assunto com ênfase sobre a aplicação da transformada wavelet a vários ramos da ciência é,

Paul S. Addison. The Illustrated Wavelet Transform Handbook. Institute of Physics Publishing (2002), ISBN 0750306920.

Para cobertura extensiva de análise de sinal usando wavelets, coleções de wavelet e bases de cosseno local veja,

S. G. Mallat. A wavelet tour of signal processing (Second edition). Academic Press (1999), ISBN 012466606X.

O conceito de análise de multiresolução básico na transformada wavelet é descrito em,

S. G. Mallat. Multiresolution Approximations and Wavelet Orthonormal Bases of L^2(R). Transactions of the American Mathematical Society, 315(1), 1989, 69–87.

S. G. Mallat. A Theory for Multiresolution Signal Decomposition—The Wavelet Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11, 1989, 674–693.

Os coeficientes para as famílias de wavelets individuais implementados pela biblioteca podem ser encontrados nos seguintes artigos,

I. Daubechies. Orthonormal Bases of Compactly Supported Wavelets. Communications on Pure and Applied Mathematics, 41 (1988) 909–996.

A. Cohen, I. Daubechies, and J.-C. Feauveau. Biorthogonal Bases of Compactly Supported Wavelets. Communications on Pure and Applied Mathematics, 45 (1992) 485–560.

O arquivo da PhysioNet de conjuntos de dados fisiológicos pode ser encontrado online em http://www.physionet.org/ e é descrito no seguinte artigo,

Goldberger et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 101(23):e215-e220 2000.

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.