| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Técnicas de busca estocástica são usadas quando a estrutura de um espaço não é bem entendida ou não é plana, de forma que técnicas como o método de Newton (que requer cálculo de matrizes jacobianas derivadas) não podem ser usadas. Particularmente, essas técnicas são frequêntemente usadas para resolver problemas de otimização combinatorial, tais como o problema do caixeiro viajante (49).
O objetivo é encontrar um ponto no espaço no qual um valor real função de energia (ou função de custo) é minimizado. Anelamento simulado é uma técnica de minimização que tem fornecido resultados evitando mínimo local; é baseado na idéia de que fazendo uma caminhada aleatória através do espaço em sucessivamente baixas temperaturas, onde a probabilidade de dar um passo é fornecido por uma distribuição de Boltzmann.
As funções descritas nesse capítulo são declaradas no arquivo de cabeçalho ‘gsl_siman.h’.
| 25.1 Algoritmo de Anelamento simulado | ||
| 25.2 Funções de Anelamento Simulado | ||
| 25.3 Exemplos | ||
| 25.4 Referências e Leituras Adicionais |
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O algoritmo de anelamento simulado pega caminhadas aleatórias através do espaço
do problema, buscando pontos com baixas energias; nessa caminhada aleatória, a
probabilidade de dar um passo é determinada pela distribuição de Boltzmann,
|
Em outras palavras, um passo irá ocorrer se a nova energia for menor. Se a nova energia for maior, a transição pode ainda ocorrer, e sua possibilidade é proporcional à T e inversamente proporcional à diferença de energia E_{i+1} - E_i.
A temperatura T é inicialmente ajustada para um valor alto, e uma caminhada aleatória é realizada naquela temperatura. Então a temperatura é diminuída muito lentamente conforme uma agenda de resfriamento, por exemplo: T -> T/mu_T onde \mu_T é ligeiramente maior que 1.
A pequena probabilidade de dar um passo que fornece alta energia é o que permite ao anelamento simulado frequentemente saia do mínimo local.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função executa uma busca de anelamento simulado através de um dado espaço. O espaço é especificado fornecendo as funções Ef e distance. Os passos do anelamento simulado são gerados usando o gerador de números aleatórios r e a função take_step.
A configuração inicial do sistema deve ser dada por x0_p.
A rotina oferece dois modos para atualizar configurações, um modo de tamanho
fixo e um modo de tamanho variável. No modo de tamanho fixo a configuração
é armazenada como um bloco simples de memória de tamanho element_size.
Cópias dessa configuração são criadas, copiadas e destruídas
internamente usando as funções da biblioteca C padrão malloc,
memcpy e free. Os apontadores de função copyfunc,
copy_constructor e destructor devem ser apontadores nulos no
modo de tamanho fixo. No modo de tamanho variável as funções
copyfunc, copy_constructor e destructor são usadas para
criar, copiar e destruir configuraçãoes internamente. A variável
element_size deve ser zero no modo de tamanho variável.
A estrutura params (descrita abaixo) controla a execução fornecendo o agendamento de temperatura e outros parâmetros configuráveis para o algoritmo.
Na saída o melhor resultado encontrado durante a busca é colocado em
*x0_p. Se o processo de anelamento tiver obtido sucesso esse
*x0_p deve ser uma boa aproximação para o ponto ótimo no espaço.
Se o apontador de função print_position for nulo, um relatório de
depuração irá ser mostrado para stdout com as seguintes colunas:
#-iter #-evals temperature position energy best_energy
e a saída da função print_position propriamente dita. Se print_position for nulo então nenhuma informação é mostrada.
As rotinas de anelamento simulado requerem muitas funções fornecidas pelo usuário para definir o espaço de configuração e a função de energia. Os protótipos para essas funções são fornecidos abaixo.
Esse tipo de função retorna a energia de uma configuração xp.
double (*gsl_siman_Efunc_t) (void *xp)
Esse tipo de função deve modificar a configuração xp usando um passo aleatório tomado a partir do gerador r, atém uma distância máxima de step_size.
void (*gsl_siman_step_t) (const gsl_rng *r, void *xp,
double step_size)
Esse tipo de função deve retornar a distância entre duas configurações xp e yp.
double (*gsl_siman_metric_t) (void *xp, void *yp)
Esse tipo de função deve mostrar os conteúdos da configuração xp.
void (*gsl_siman_print_t) (void *xp)
Esse tipo de função deve copiar a configuração source para dest.
void (*gsl_siman_copy_t) (void *source, void *dest)
Esse tipo de função deve criar uma nova cópia da configuração xp.
void * (*gsl_siman_copy_construct_t) (void *xp)
Esse tipo de função deve destruir a configuração xp, liberando sua memória.
void (*gsl_siman_destroy_t) (void *xp)
Esses são os parâmetros que controlam uma execução de gsl_siman_solve.
Essa estrutura contém todas as informações necessárias para controlar a
busca, além da função de energia, a função de passo e a suposição
inicial.
int n_triesO número de pontos a serem tentados para cada passo.
int iters_fixed_TO número de iterações a cada temperatura.
double step_sizeO tamanho máximo do passo na caminhada aleatória.
double k, t_initial, mu_t, t_minOs parâmetros da distribuição de Boltzmann e agenda de resfriamento.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O pacote de anelamento simulado é desajeitado, e tem de ser pelo fato de ser escrito em C, para chamadores C, e tenta ser polimórfico ao memso tempo. Mas aqui fornecemos alguns exemplos que podem ser colados em sua aplicação com pequenas modificações e que deve tornar as coisas mais fáceis.
| 25.3.1 Exemplo trivial | ||
| 25.3.2 O Problema do Caixeiro Viajante |
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O primeiro exemplo, no espaço unidimensional (50) de Renè Descartes, ajusta-se uma função de energia que é uma onda senóidal amortecida; temos muitos mínimos locais, mas somente um mínimo global, algum lugar entre 1.0 e 1.5. A suposição inicial fornecida é 15.5, que está muitos mínimos locais adiante do mínimo global.
#include <math.h>
#include <stdlib.h>
#include <string.h>
#include <gsl/gsl_siman.h>
/* set up parameters for this simulated annealing run */
/* how many points do we try before stepping */
#define N_TRIES 200
/* how many iterations for each T? */
#define ITERS_FIXED_T 1000
/* max step size in random walk */
#define STEP_SIZE 1.0
/* Boltzmann constant */
#define K 1.0
/* initial temperature */
#define T_INITIAL 0.008
/* damping factor for temperature */
#define MU_T 1.003
#define T_MIN 2.0e-6
gsl_siman_params_t params
= {N_TRIES, ITERS_FIXED_T, STEP_SIZE,
K, T_INITIAL, MU_T, T_MIN};
/* now some functions to test in one dimension */
double E1(void *xp)
{
double x = * ((double *) xp);
return exp(-pow((x-1.0),2.0))*sin(8*x);
}
double M1(void *xp, void *yp)
{
double x = *((double *) xp);
double y = *((double *) yp);
return fabs(x - y);
}
void S1(const gsl_rng * r, void *xp, double step_size)
{
double old_x = *((double *) xp);
double new_x;
double u = gsl_rng_uniform(r);
new_x = u * 2 * step_size - step_size + old_x;
memcpy(xp, &new_x, sizeof(new_x));
}
void P1(void *xp)
{
printf ("%12g", *((double *) xp));
}
int
main(int argc, char *argv[])
{
const gsl_rng_type * T;
gsl_rng * r;
double x_initial = 15.5;
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc(T);
gsl_siman_solve(r, &x_initial, E1, S1, M1, P1,
NULL, NULL, NULL,
sizeof(double), params);
gsl_rng_free (r);
return 0;
}
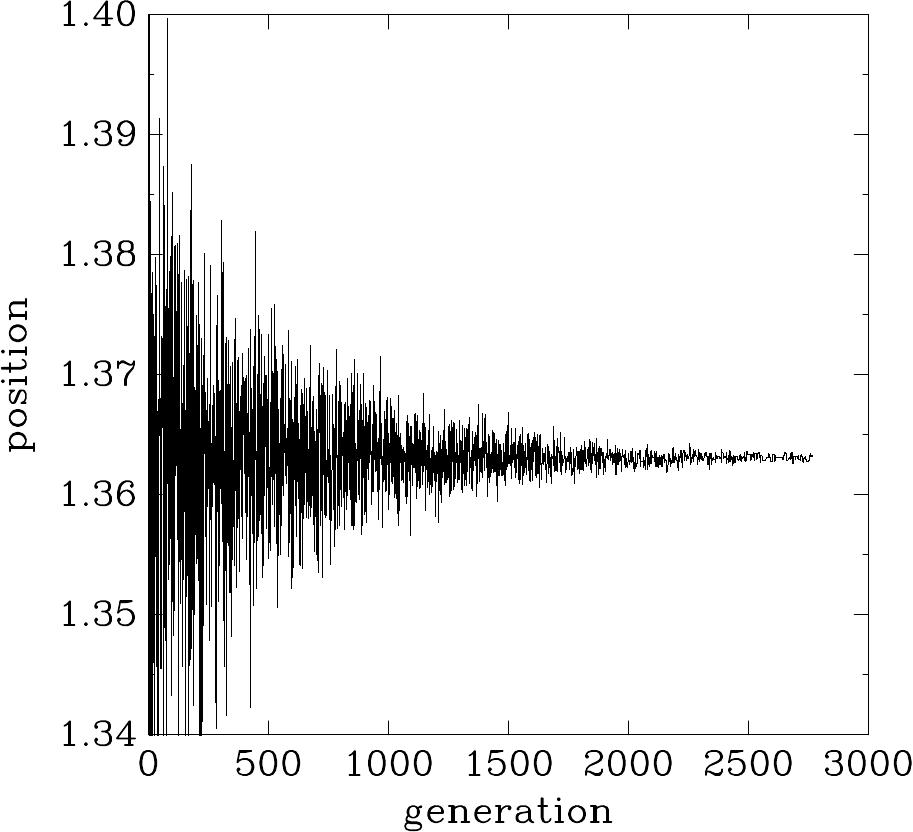
Aqui está alguns dos gráficos que são gerados pela execução de
siman_test da seguinte forma:
$ ./siman_test | awk '!/^#/ {print $1, $4}'
| graph -y 1.34 1.4 -W0 -X generation -Y position
| plot -Tps > siman-test.eps
$ ./siman_test | awk '!/^#/ {print $1, $5}'
| graph -y -0.88 -0.83 -W0 -X generation -Y energy
| plot -Tps > siman-energy.eps

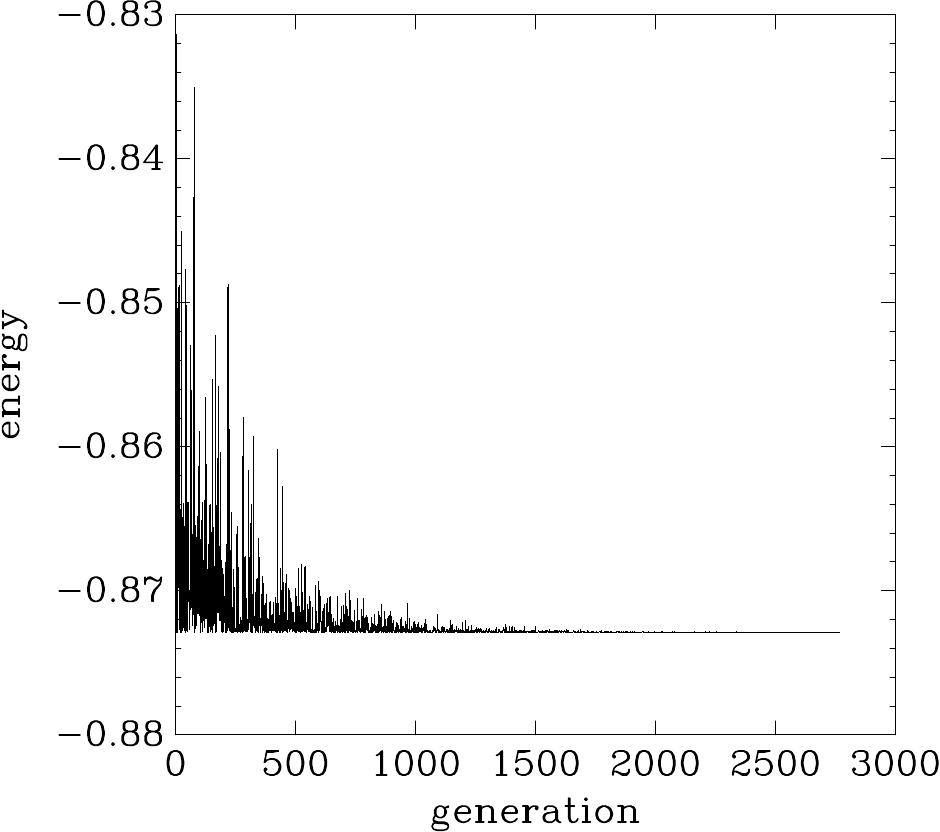
Exemplo de uma execução de anelamento simulado: em altas temperaturas (anteriormente ao gráfico) você vê que a solução pode flutuar, mas a baixas temperaturas a solução converge.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O PCV (Problema do Caixeiro Viajante) é o problema clássico de otimização combinatorial (51). Segue adiante uma versão muito simples do PCV, baseada em coordenadas de doze cidades no sudoeste dos Estados Unidos. Essa versão pode ser chamada o Problema do Caixeiro voador, uma vez que estou usando o grande círculo distância entre cidades, em lugar da kilometragem. Também: Eu assumi que a terra é uma esfera, de forma que Eu não usei distâncias da geóide.
A rotina gsl_siman_solve encontra uma rota que mede
3490.62 Kilômetros; essa medida é confirmada por uma busca exaustiva de todas
as possíveis rotas com a mesma cidade inicial.
O código completo pode ser encontrado em ‘siman/siman_tsp.c’, mas Eu inclui aqui alguns gráficos gerados da seguinte forma:
$ ./siman_tsp > tsp.output
$ grep -v "^#" tsp.output
| awk '{print $1, $NF}'
| graph -y 3300 6500 -W0 -X generation -Y distance
-L "TSP - 12 southwest cities"
| plot -Tps > 12-cities.eps
$ grep initial_city_coord tsp.output
| awk '{print $2, $3}'
| graph -X "longitude (- means west)" -Y "latitude"
-L "TSP - initial-order" -f 0.03 -S 1 0.1
| plot -Tps > initial-route.eps
$ grep final_city_coord tsp.output
| awk '{print $2, $3}'
| graph -X "longitude (- means west)" -Y "latitude"
-L "TSP - final-order" -f 0.03 -S 1 0.1
| plot -Tps > final-route.eps
Essa é a saída mostrando a ordem inicial da cidades; a longitude é negativa, uma vez que é oeste e desejo o gráfico visto como um mapa.
# initial coordinates of cities (longitude and latitude) ###initial_city_coord: -105.95 35.68 Santa Fe ###initial_city_coord: -112.07 33.54 Phoenix ###initial_city_coord: -106.62 35.12 Albuquerque ###initial_city_coord: -103.2 34.41 Clovis ###initial_city_coord: -107.87 37.29 Durango ###initial_city_coord: -96.77 32.79 Dallas ###initial_city_coord: -105.92 35.77 Tesuque ###initial_city_coord: -107.84 35.15 Grants ###initial_city_coord: -106.28 35.89 Los Alamos ###initial_city_coord: -106.76 32.34 Las Cruces ###initial_city_coord: -108.58 37.35 Cortez ###initial_city_coord: -108.74 35.52 Gallup ###initial_city_coord: -105.95 35.68 Santa Fe
A rota ótima termina sendo:
# final coordinates of cities (longitude and latitude) ###final_city_coord: -105.95 35.68 Santa Fe ###final_city_coord: -103.2 34.41 Clovis ###final_city_coord: -96.77 32.79 Dallas ###final_city_coord: -106.76 32.34 Las Cruces ###final_city_coord: -112.07 33.54 Phoenix ###final_city_coord: -108.74 35.52 Gallup ###final_city_coord: -108.58 37.35 Cortez ###final_city_coord: -107.87 37.29 Durango ###final_city_coord: -107.84 35.15 Grants ###final_city_coord: -106.62 35.12 Albuquerque ###final_city_coord: -106.28 35.89 Los Alamos ###final_city_coord: -105.92 35.77 Tesuque ###final_city_coord: -105.95 35.68 Santa Fe
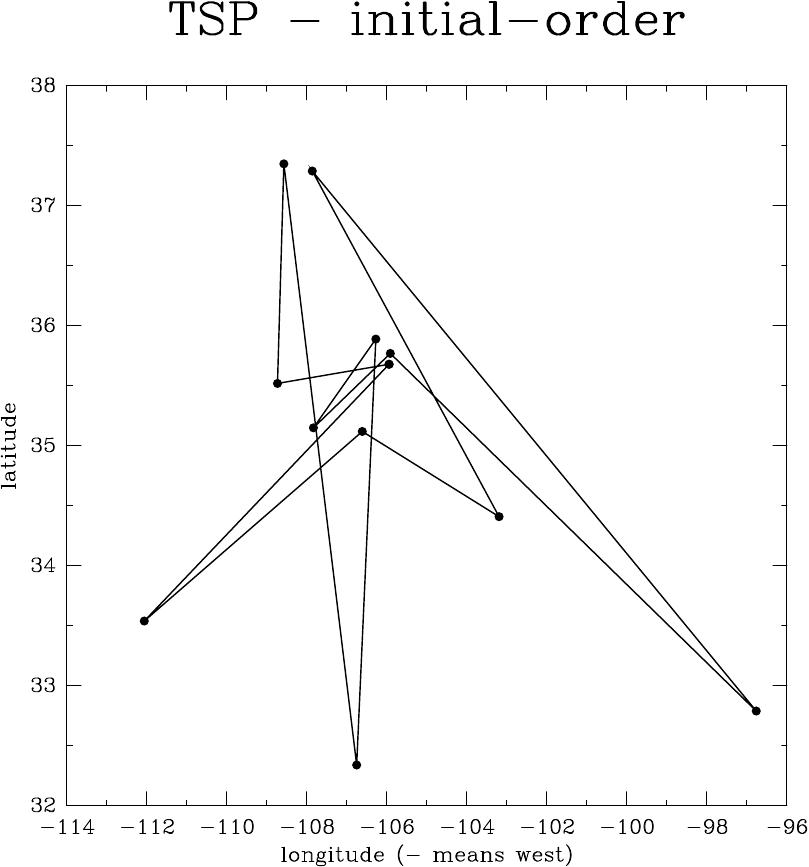
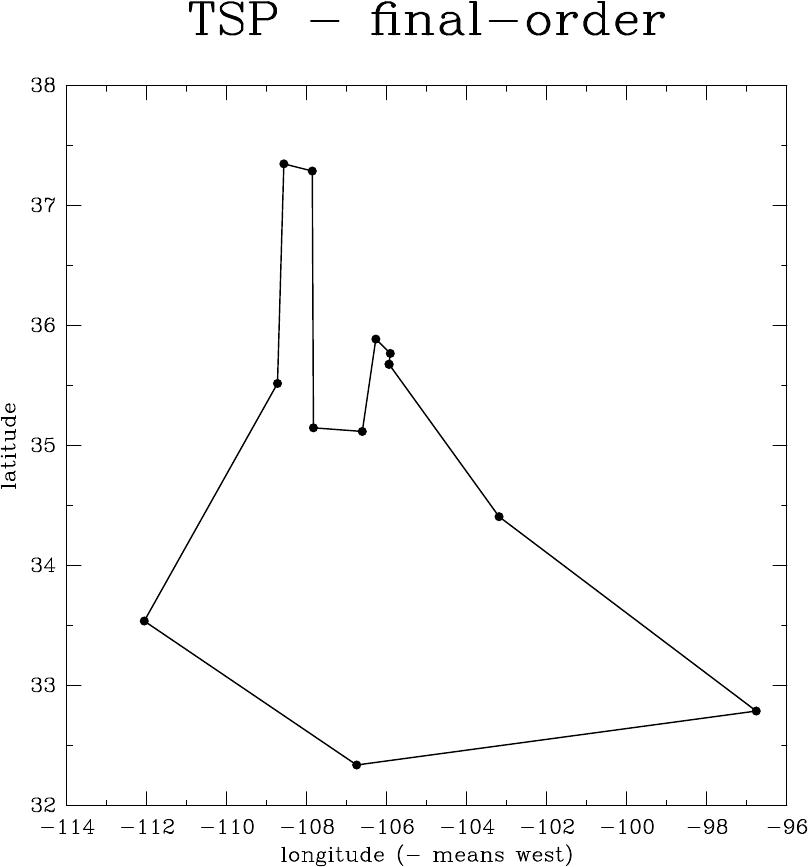
Rota inicial e final (ótima) para as 12 cidades do sudoeste do Problema do Caixeiro Voador.
Aqui está um gráfico da função de custo (energia) versus geração (ponto do cálculo no qual uma nova temperatura é ajustada) para esse problema:
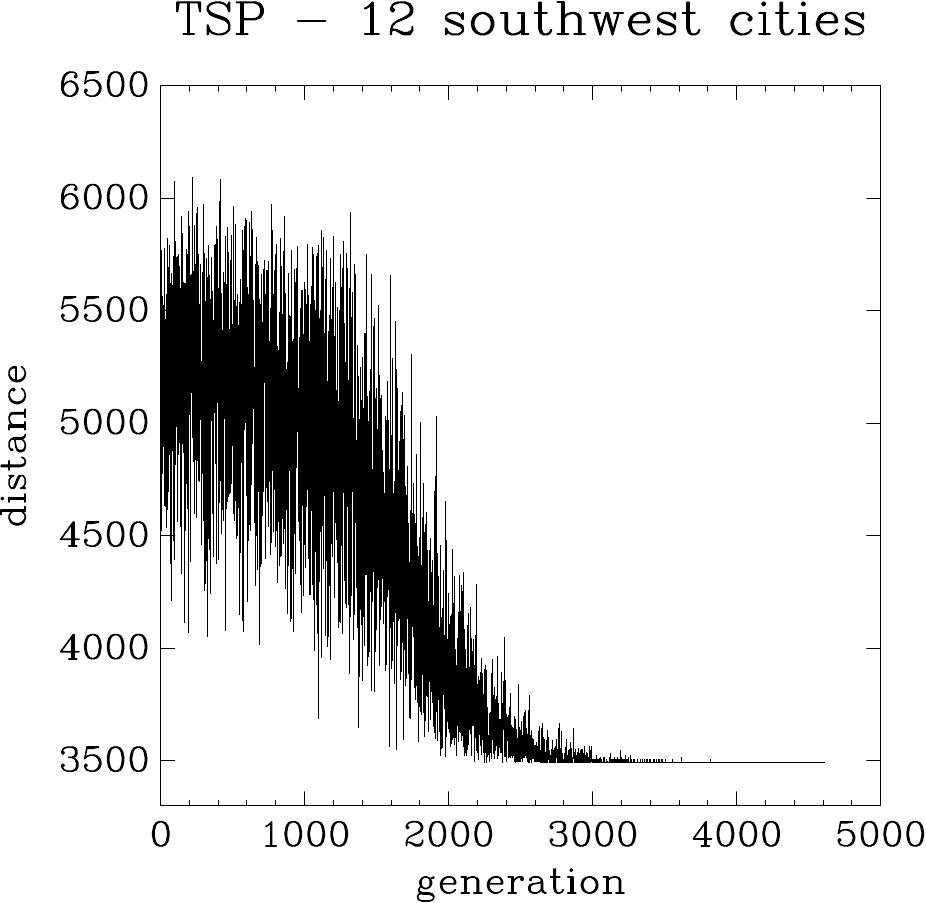
Exemplo de uma execução de anelamento simulado para as 12 cidades do sudoeste do Problema do Caixeiro Viajante.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Informação adicional está disponível no seguinte livro,
| [ << ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.