26 Equações Diferenciais Ordinárias

Esse capítulo descreve funções para resolver equações diferenciais ordinárias (EDO) em problemas de valor inicial. A biblioteca fornece uma variedade de métodos de baixo nível, tais como as rotinas de Runge-Kutta e Bulirsch-Stoer, e componenetes de alto nível para controle adaptativo do tamanho do degrau. Os componentes podem ser combinados pelo usuário para encontrar a solução desejada, com acesso completo a qualquer passo intermediário. Um objeto norteador pode ser usado como um contêiner de alto nível para facilmente usar das funções de baixo nível.

Essas funções são declaradas no arquivo de cabeçalho ‘gsl_odeiv2.h’. Essa é uma nova interface na versão 1.15 e usa o prefixo gsl_odeiv2 para todas as funções. É recomendado o uso da implementação atual em relação à implementação anterior gsl_odeiv definida em ‘gsl_odeiv.h’ A interface antiga foi mantida com o nome original por questões de compatibilidade com as versões anteriores.

26.1 Definindo um Sistema de EDOs

As rotinas resolvem o sistema geral de primeira ordem n-dimensional,

dy_i(t)

= f_i (t, y₁(t), ... y_n(t))

para i = 1, \dots, n. As funções degrau garantem o vetor de derivadas f_i e a matriz de Jacobi, J_{ij} = df_i(t,y(t)) / dy_j. Um sistema de equações é definido usando o tipo de dado gsl_odeiv2_system.

Data Type: gsl_odeiv2_system

Esse tipo de dado define um sistema de EDO genérico com parâmetros arbitrários.

int (* function) (double t, const double y[], double dydt[], void * params)

Essa função deve armazenar os elementos do vetor f_i(t,y,params) no vetor estático dydt, para argumentos (t,y) e parâmetros params.

A função deve retornar GSL_SUCCESS se o cálculo for completado com sucesso. Qualquer outro valor de retorno indica um erro. Um valor de retorno especial GSL_EBADFUNC faz com que rotinas gsl_odeiv2 parem imediatamente e retorne. O usuário deve chamar uma função apropriada para zerar onde for necessário (e.g. gsl_odeiv2_driver_reset ou gsl_odeiv2_step_reset) antes de continuar. Use valores de retorno diferentes dos códigos de erro padronizados da GSL para distinguir sua função como a fonte do erro.

int (* jacobian) (double t, const double y[], double * dfdy, double dfdt[], void * params);

Essa função deve armazenar o vetor de elementos da derivada no vetor estático dfdt e a matriz de Jacobi J_{ij} no vetor estático dfdy, tratada como uma matriz linha ordenada J(i,j) = dfdy[i * dimension + j] onde dimension é a dimensão do sistema.

Alguns dos algoritmos de degrau de gsl_odeiv2 não fazem uso da matriz de Jacobi, de forma que pode não ser necessário fornecer esse elementos de função (a jacobian da estrutura pode ser substituída por um apontador nulo nos referidos algoritmos).

A função deve retornar GSL_SUCCESS se o cálculo for completado com sucesso. Qualquer outro valor de retorno indica um erro. Um valor de retorno especial GSL_EBADFUNC faz com que rotinas gsl_odeiv2 parar imediatamente e retornar. O usuário deve chamar uma função apropriada para zerar o que for necessário (e.g. gsl_odeiv2_driver_reset ou gsl_odeiv2_step_reset) antes de continuar. Use valores de retorno diferentes dos códigos de retorno padronizados da GSL para distinguir sua função como a fonte do erro.

size_t dimension;

Essa é a dimensão do sistema de equações.

void * params

Esse é um apontador para os parâmetros arbitrários do sistema.

26.2 Funções Degrau

Os componenetes de mais baixo nível são as funções degrau que avançam uma solução do tempo t a t+h para um tamnho de degrau fixo h e estimativa do erro local resultante.

Function: gsl_odeiv2_step * gsl_odeiv2_step_alloc (const gsl_odeiv2_step_type * T, size_t dim): Essa função retorna uma apontador para uma instância alocada recentemente de uma função de degrau do tipo T para um sistema de dim dimensões. Por favor note que se você usar um método de fazer degrau que requer acesso a um objeto norteador, é aconselhável usar um método de método de alocação de driver norteador, que automaticamente aloca uma função degrau, também.

Function: int gsl_odeiv2_step_reset (gsl_odeiv2_step * s): Essa função ajusta em zero a função degrau s. Pode ser usada sempre que o seguinte uso de s não seja uma continuação de um passo dado anteriormente.

Function: void gsl_odeiv2_step_free (gsl_odeiv2_step * s): Essa função libera toda a memória associada com a função degrau s.

Function: const char * gsl_odeiv2_step_name (const gsl_odeiv2_step * s)

essa função retorna um apontador para o nome da função degrau. Por exemplo,

printf ("o metodo de degrau é '%s'\n",
         gsl_odeiv2_step_name (s));

pode imprimir alguma coisa como o metodo de degrau é 'rkf45'.

Function: unsigned int gsl_odeiv2_step_order (const gsl_odeiv2_step * s): Essa função retorna a ordem da função degrau sobre o degrau anterior. A ordem pode variar se a função degrau propriamente dita for adaptativa.

Function: int gsl_odeiv2_step_set_driver (gsl_odeiv2_step * s, const gsl_odeiv2_driver * d): Essa função ajusta um apontador de um objeto norteador d para a função degrau s, para permitir que a função degrau acesse objeto de controle (e evolua) através do objeto norteador. Esse é um requerimento para algumas funções degrau, pegar o nível de erro desejado para iteração interna da função de degrau. Alocação de um objeto norteador chama essa função automaticamente.

Function: int gsl_odeiv2_step_apply (gsl_odeiv2_step * s, double t, double h, double y[], double yerr[], const double dydt_in[], double dydt_out[], const gsl_odeiv2_system * sys)

Essa função aplica a função degrau s para o sistema de equações definido por sys, usando o tamanho de degrau h para avançar o sistema a partir do tempo t e estado y até o tempo t+h. O novo estado do sistema é armazenado em y na saída, com uma estimativa do erro absoluto em cada componente armazenada em yerr. Se o argumento dydt_in não for nulo deve apontar um vetor estático contendo as derivadas para o sistema no tempo t na saída. É opcional como as derivadas irão ser calculadas internamente se elas não forem fornecidas, mas permite o reuso de informação de derivada existente. Na saída as novas derivadas do sistema no tempo t+h irão ser armazenadas em dydt_out se não forem nulas.

A função degrau retorna GSL_FAILURE se for incapaz de calcular o degrau requisitado. Também, se as funções fornecidas pelo usuário definidas no sistema sys retornarem situação atual outra que não GSL_SUCCESS o degrau irá ser abortado. Nesse caso, os elementos de y irão ser restaurados para seus valores anteriores e o código de erro a partir da função fornecida pelo usuário irá ser retornado. Falha pode ser devido a uma singularidade no sistema ou devido a tamanho de degrau h muito grande. Nesse caso o degrau deve ser tentado novamente com um tamanho de degrau menor, e.g. h/2.

Se o objeto norteador não for apropriadamente ajustado via gsl_odeiv2_step_set_driver para aqueles degraus que precisam dele, a função degrau retorna GSL_EFAULT. Se as funções fornecidas pelo usuário definidas no sistema sys retornarem GSL_EBADFUNC, a função retorna imediatamente com o mesmo código de retorno. Nesse casp o usuário deve chamar gsl_odeiv2_step_reset antes de chamar essa função novamente.

Os seguintes algoritmos estão disponíveis,

Step Type: gsl_odeiv2_step_rk2: Método Runge-Kutta (2, 3) embutido explícito.

Step Type: gsl_odeiv2_step_rk4: Método Runge-Kutta explícito de quarta ordem (clássico). Estimativa de erro é realizada pelo método duplicação de degrau. Para estimativa mais eficiente do erro, use os métodos embutidos descritos abaixo.

Step Type: gsl_odeiv2_step_rkf45: Método Runge-Kutta-Fehlberg (4, 5) embutido explícito. Esse método é um bom integrador de propósito geral.

Step Type: gsl_odeiv2_step_rkck: Método Runge-Kutta Cash-Karp (4, 5) embutido explícito.

Step Type: gsl_odeiv2_step_rk8pd: Método Runge-Kutta Prince-Dormand (8, 9) embutido explícito.

Step Type: gsl_odeiv2_step_rk1imp: De Gauss implícito Runge-Kutta de primeira ordem. Também conhecido com Euler Implícito ou método de Euler ao contrário. Estimação de erro é realizada pelo método do degrau duplo. O algoritmo requer o Jacobiano e acesso ao objeto norteador via gsl_odeiv2_step_set_driver.

Step Type: gsl_odeiv2_step_rk2imp: De Gauss implícito Runge-Kutta de segunda ordem. Também conhecido como regra do ponto médio implícito. Estimação de erro é realizada pelo método do degrau duplo. Essa função degrau requer o Jacobian e acesso ap objeto norteador via gsl_odeiv2_step_set_driver.

Step Type: gsl_odeiv2_step_rk4imp: De Gauss implícito Runge-Kutta de quarta ordem. Estimação de erro é realizada pelo método do degrau duplo. Esse algoritmo requer o Jacobiano e acesso ao objeto norteador via gsl_odeiv2_step_set_driver.

Step Type: gsl_odeiv2_step_bsimp: Método de Bulirsch-Stoer implícito de Bader e Deuflhard. O método é geralmente adequado para problemas de rigidez. Essa função degrau requer o Jacobian.

Step Type: gsl_odeiv2_step_msadams: Um método de Adams de degrau múltiplo linear coeficiente variável na forma Nordsieck. Essa função degrau usa os métodos Adams-Bashforth (estimador) explícito e Adams-Moulton implícito (corretor) em P(EC)^m modo iteração funcional. A ordem do método varia dinamicamente entre 1 e 12. Essa função degrau requer o acesso ao objeto norteador via gsl_odeiv2_step_set_driver.

Step Type: gsl_odeiv2_step_msbdf: Um método de fórmula de diferenciação ao contrário linear de coeficiente variável (BDF) (52) na forma de Nordsieck. Essa função degrau usa a fórmula explícita BDF como estimador e a fórmula BDF implícita como corretor. Um método modificado de iteração de Newton é usado para resolver o sistema de equações não lineares. A ordem do método varia dinamicamente entre 1 e 5. O método é geralmente adequado para problemas de rigidez. Essa função degrau requer o Jacobiano e o acesso ao objeto norteador via gsl_odeiv2_step_set_driver.

26.3 Controle Adaptativo de Tamanho do Degrau

A função de controle examina a mudança proposta para a solução produzidoa por uma função degrau e tenta determinar o tamanho de degrau ótimo para um nível de erro especificado pelo usuário.

Function: gsl_odeiv2_control * gsl_odeiv2_control_standard_new (double eps_abs, double eps_rel, double a_y, double a_dydt)

O objeto de controle padrão é uma heurística de quatro parâmetros baseada nos erros absoluto e relativo eps_abs e eps_rel, e fatores de ajuste proporcional a_y e a_dydt para o estado do sistema y(t) e derivadas y'(t) respectivamente.

O procedimento de ajuste do tamanho do degrau por esse método inicia-se calculando o nível desejado de erro D_i para cada componente,

D_i = ϵ_abs + ϵ_rel * (a_y |y_i| + a_dydt h |y′_i|)

e comparando com o erro observado E_i = |yerr_i|. Se o erro observado E exceder o nível desejado de erro D por mais que 10% para qualquer componente então o método reduz o tamanho de degrau por um fator apropriado,

h_new = h_old * S * (E/D)^−1/q

onde q é a ordem de consistência do (e.g. q=4 para 4(5) RK embutido), e S é um fator seguro de 0.9. A razão E/D é tomada para ser a maior entre as razões E_i/D_i.

Se o erro observado E for maior que 50% do nível de erro desejado D para a maior razão E_i/D_i então o algoritmo tem a oportunidade de aumentar o tamanho do degrau para trazer o erro para próximo do nível desejado,

h_new = h_old * S * (E/D)^−1/(q+1)

Isso engloba todos os métodos padronizados de ajuste proporcional de erro. Para evitar mudanças descontroladas no tamanho do degrau, o fator médio de ajuste proporcional é limitado ao intervalo de 1/5 a 5.

Function: gsl_odeiv2_control * gsl_odeiv2_control_y_new (double eps_abs, double eps_rel): Essa função cria um novo objeto de controle que irá manter o erro local sobre cada degrau dentro de um erro absoluto de eps_abs e erro relativo de eps_rel com relação ã solução y_i(t). Isso é equivalente ao objeto padrão de controle com a_y=1 e a_dydt=0.

Function: gsl_odeiv2_control * gsl_odeiv2_control_yp_new (double eps_abs, double eps_rel): Essa função cria um novo objeto de controle que irá manter o erro local sobre cada degrau dentro do erro absoluto de eps_abs e erro relativo de eps_rel com relação a derivadas da solução y'_i(t). Isso é equivalente ao objeto de controle padrão com a_y=0 e a_dydt=1.

Function: gsl_odeiv2_control * gsl_odeiv2_control_scaled_new (double eps_abs, double eps_rel, double a_y, double a_dydt, const double scale_abs[], size_t dim)

Essa função cria um novo objeto de controle que usa o mesmo algoritmo que gsl_odeiv2_control_standard_new mas com um erro absoluto que é ajustado proporcionalmente para cada componente pelo vetor estático scale_abs. A fórmula para D_i para esse objeto de controle é,

D_i = ϵ_abs s_i + ϵ_rel * (a_y |y_i| + a_dydt h |y′_i|)

onde s_i é o i-ésimo componente do vetor estático scale_abs. A mesma heurística de controle de erro é usada pelo ODE do software Matlab.

Function: gsl_odeiv2_control * gsl_odeiv2_control_alloc (const gsl_odeiv2_control_type * T): Essa função retorna um apontador para uma intância recentemente alocada de uma função de controle do tipo T. Essa função é necessária somente para definir novos tipos de funções de controle. Para a maioria dos propósitos as funções de controle padrão descritas acima devem ser suficientes.

Function: int gsl_odeiv2_control_init (gsl_odeiv2_control * c, double eps_abs, double eps_rel, double a_y, double a_dydt): Essa função inicializa a função de controle c com os parâmetros eps_abs (erro absoluto), eps_rel (erro relativo), a_y (fator de ajuste proporcional para y) e a_dydt (fator de ajuste proporcional paraderivadas).

Function: void gsl_odeiv2_control_free (gsl_odeiv2_control * c): Essa função libera toda a memória associada ã função de controle c.

Function: int gsl_odeiv2_control_hadjust (gsl_odeiv2_control * c, gsl_odeiv2_step * s, const double y[], const double yerr[], const double dydt[], double * h): Essa função ajusta o tamanho do degrau h usando a função de controle c, e os valores atuais de y, yerr e dydt. A função degrau step é também necessária para determinar a ordem do método. Se o erro nos valores de y yerr forem avaliados como sendo muito grandes então o tamanho de degrau h é reduzido e a função retorna GSL_ODEIV_HADJ_DEC. Se o erro for suficientemente pequeno então h pode ser aumentado e o código GSL_ODEIV_HADJ_INC é retornado pela função. A função retorna GSL_ODEIV_HADJ_NIL se o tamanho do degrau permanecer inaterado. O objetivo da função é estimar o maior tamanho de degrau que satisfaz a expectativa de precisão especificada pelo usuário para o ponto atual.

Function: const char * gsl_odeiv2_control_name (const gsl_odeiv2_control * c)

Essa função retorna um apontador para o nome da função de controle. Por exemplo,

printf ("o método de controle é '%s'\n", 
        gsl_odeiv2_control_name (c));

pode imprimir alguma coisa como o método de controle é 'standard'

Function: int gsl_odeiv2_control_errlevel (gsl_odeiv2_control * c, const double y, const double dydt, const double h, const size_t ind, double * errlev): Essa função calcula o nível de erro desejado do ind-ésimo componente para errlev. É necessário o valor (y) e o valor da derivada (dydt) da componente, e o atual tamanho de degrau h.

Function: int gsl_odeiv2_control_set_driver (gsl_odeiv2_control * c, const gsl_odeiv2_driver * d): Essa função ajusta um apontador do objeto norteador d para o objeto de controle c.

26.4 Evolução

A função evolution combina os resultados de uma função degrau e de uma função de controle para de forma confiável avançar a solução para adiante de um degrau usando um tamanho de degrau aceitável.

Function: gsl_odeiv2_evolve * gsl_odeiv2_evolve_alloc (size_t dim): Essa função retorna um apontador para uma instância recentemente alocada de uma função de evolução para um sistema de dim dimensões.

Function: int gsl_odeiv2_evolve_apply (gsl_odeiv2_evolve * e, gsl_odeiv2_control * con, gsl_odeiv2_step * step, const gsl_odeiv2_system * sys, double * t, double t1, double * h, double y[])

Essa função avança o sistema (e, sys) a partir do tempo t e da posição y usando a função degrau step. O novo tempo e posição é armazenado em t e y na saída.

O tamanho de degrau inicial é tomado como h. A função de controle con é aplicada para verificar se o erro local estimado pela função degrau step usando tamanho de degrau h excede a tolerância de erro requerida. Se o erro é muito alto, o degrau é ajustado por meio de uma chamada a step com um decrescimo do tamanho de degrau. Esse proceso é feito até que um tamanho de degrau aceitável seja encontrado. Uma estimativa do erro local para o degrau pode ser obtido a partir das componentes do vetor estático e->yerr[].

Se as funções fornecidas pelo usuário definidas no sistema sys retornarem GSL_EBADFUNC, a função retorna imediatamente com o mesmo código de retorno. Nesse caso o usuário deve chamar gsl_odeiv2_step_reset e gsl_odeiv2_evolve_reset antes de chamar essa função novamente.

De outra forma, se as funções fornecidas pelo usuário definidas no sistema sys ou a função degrau step retornar uma situação atual outra que não GSL_SUCCESS, o degrau é ajustado com um decrescimo de tamanho de degrau. Se o tamanho de degrau vier a decrecer abaixo da precisão da máquina onde a gsl estiver sendo executada, um código GSL_FAILURE é retornado se as funções do usuário retornarem GSL_SUCCESS. De outra forma o valor retornado pela função de usuário é retornado. Se nenhum degrau aceitável puder ser feito, t e y irão ser restaurados a seus valores de degrau anteriores e h conterá o tamanho de degrau final tantado anteriormente.

Se o degrau obtiver sucesso a função retorna um tamanho de degrau sugerido para o próximo degrau em h. O tempo máximo t1 é garantidamente não ser ultrapassado pelo tempo de degrau. Sobre o tempo final de degrau o valor de t irá ser ajustado para t1 exatamente.

Function: int gsl_odeiv2_evolve_apply_fixed_step (gsl_odeiv2_evolve * e, gsl_odeiv2_control * con, gsl_odeiv2_step * step, const gsl_odeiv2_system * sys, double * t, const double h, double y[]): Essa função avança o sistema de EDO (e, sys, con) a partir do tempo t e da posição y usando a função degrau step usando o tamanho de degrau especificado h. Se o erro local estimado pela função degrau exceder o nível de erro desejado, o degrau não é executado e a função retorna GSL_FAILURE. De outra forma o valor retornado pela função de usuário é retornado.

Function: int gsl_odeiv2_evolve_reset (gsl_odeiv2_evolve * e): Essa função ajusta a função de evolução e. Pode ser usada sempre que o próximo uso de e não for uma continuação de um degrau anterior.

Function: void gsl_odeiv2_evolve_free (gsl_odeiv2_evolve * e): Essa função liberal toda memória associada à função de evolução e.

Function: int gsl_odeiv2_evolve_set_driver (gsl_odeiv2_evolve * e, const gsl_odeiv2_driver * d): Essa função ajusta um apontador do objeto norteador d para o objeto de evolução e.

Se um sistema tem mudanças descontínuas nas derivadas em pontos conhecidos, adverte-se para evoluir o sistema entre cada descontinuidade sequencialmente. Por exemplo, se uma mudança de degrau em um norteador externo força ocorrências nos tempos t_a, t_b e t_c então a evolução deve ser realizda sobre os intervalos (t_0,t_a), (t_a,t_b), (t_b,t_c), e (t_c,t_1) separadamente e não diretamente sobre o intervalo (t_0,t_1).

26.5 Norteador

O objeto norteador é um invólucro que combina a evolução, o controle e objetos de degrau para facilitar o uso.

Function: gsl_odeiv2_driver * gsl_odeiv2_driver_alloc_y_new (const gsl_odeiv2_system * sys, const gsl_odeiv2_step_type * T, const double hstart, const double epsabs, const double epsrel)
Function: gsl_odeiv2_driver * gsl_odeiv2_driver_alloc_yp_new (const gsl_odeiv2_system * sys, const gsl_odeiv2_step_type * T, const double hstart, const double epsabs, const double epsrel)
Function: gsl_odeiv2_driver * gsl_odeiv2_driver_alloc_standard_new (const gsl_odeiv2_system * sys, const gsl_odeiv2_step_type * T, const double hstart, const double epsabs, const double epsrel, const double a_y, const double a_dydt)
Function: gsl_odeiv2_driver * gsl_odeiv2_driver_alloc_scaled_new (const gsl_odeiv2_system * sys, const gsl_odeiv2_step_type * T, const double hstart, const double epsabs, const double epsrel, const double a_y, const double a_dydt, const double scale_abs[]): Essas funções retornam um apontador para uma intância recentemente alocada de um objeto norteador. As funções automaticamente alocam e inicializam os objetos de evolução, controle e de degrau para sistemas EDO sys usando o tipo de dado de degrau T. O tamanho inicial de degrau é dado em hstart. Os argumentos restantes seguem a sintaxe e a semântica das funções de controle com o mesmo nome (gsl_odeiv2_control_*_new).

Function: int gsl_odeiv2_driver_set_hmin (gsl_odeiv2_driver * d, const double hmin): A função ajusta um menor valor de degrau permitido hmin para o norteador d. O valor padrão é 0.

Function: int gsl_odeiv2_driver_set_hmax (gsl_odeiv2_driver * d, const double hmax): A função ajusta um máximo valor de degrau permitido hmax para o norteador d. O valor padrão é GSL_DBL_MAX.

Function: int gsl_odeiv2_driver_set_nmax (gsl_odeiv2_driver * d, const unsigned long int nmax): A função ajusta um máximo valor permitido de quantidade de degraus nmax para o norteador d. O valor padrão de 0 informa que não há limite de degraus.

Function: int gsl_odeiv2_driver_apply (gsl_odeiv2_driver * d, double * t, const double t1, double y[])

Essa função evolui o sistema norteador d iniciando a evolução em t e terminando em t1. Inicialmente o vetor y deve conter os valores de variáveis dependentes no ponto t. Se a função for incapaz de completar o cálculo, um código de erro de gsl_odeiv2_evolve_apply é retornado, e t e y mostram os valores do último degrau efetuado com sucesso.

Se o número máximo de degraus for alcançado, um valor de GSL_EMAXITER é retornado. Se o tamanho do degrau cai abaixo do valor mínimo, a função retorna com GSL_ENOPROG. Se as funções fornecidas pelo usuário definidas no sistema sys retornam GSL_EBADFUNC, a fnção retorna imediatamente com o mesmo código de retorno. Nesse caso o usuário deve chamar gsl_odeiv2_driver_reset antes de chamar essa função novamente.

Function: int gsl_odeiv2_driver_apply_fixed_step (gsl_odeiv2_driver * d, double * t, const double h, const unsigned long int n, double y[]): Essa função evolui o sistema d iniciando no tempo t com n degraus de tamanho h. se a função for incapaz de completar o cálculo, um código de erro de gsl_odeiv2_evolve_apply_fixed_step é retornado, e t e y mostram os valores do último degrau efetuado com sucesso.

Function: int gsl_odeiv2_driver_reset (gsl_odeiv2_driver * d): Essa função ajusta em zero os valores dos objetos de evolução e de degrau.

Function: int gsl_odeiv2_driver_reset_hstart (gsl_odeiv2_driver * d, const double hstart): A rotina ajusta em zero os objetos de evolução e de objetos de degrau e ajusta novo tamanho inicial de degrau para hstart. Essa função pode ser usada para mudar a direção da integração.

Function: int gsl_odeiv2_driver_free (gsl_odeiv2_driver * d): Essa função libera o objeto norteador, e os objetos relacionados de evolução, de degrau e de controle.

26.6 Exemplos

O seguinte programa resolve a equação de oscilação de segunda ordem não linear de Van der Pol,

u"(t) + μu′(t) (u(t)² − 1) + u(t) = 0

Essa equação pode ser convertida em uma sistema de primeira ordem adequado para uso com as rotinas descritas nesse capítulo introduzindo uma variável separada para a velocidade, v = u'(t),

u′

= v

v′

= −u + μv (1−u²)

O programa inicia-se definindo funções para essas derivadas e seu Jacobiano. A função principal usa funções de nível norteador para resolver o problema. O programa evolui a solução de (u, v) = (1, 0) em t=0 até t=100. O tamanho de degrau h é automaticamente ajustado pelo controlador para manter uma precisão absoluta de 10^{-6} nos valores da função (u, v). O ciclo no exemplo mostra a solução nos pontos t_i = 1, 2, \dots, 100.

#include <stdio.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_odeiv2.h>

int
func (double t, const double y[], double f[],
      void *params)
{
  double mu = *(double *)params;
  f[0] = y[1];
  f[1] = -y[0] - mu*y[1]*(y[0]*y[0] - 1);
  return GSL_SUCCESS;
}

int
jac (double t, const double y[], double *dfdy, 
     double dfdt[], void *params)
{
  double mu = *(double *)params;
  gsl_matrix_view dfdy_mat 
    = gsl_matrix_view_array (dfdy, 2, 2);
  gsl_matrix * m = &dfdy_mat.matrix; 
  gsl_matrix_set (m, 0, 0, 0.0);
  gsl_matrix_set (m, 0, 1, 1.0);
  gsl_matrix_set (m, 1, 0, -2.0*mu*y[0]*y[1] - 1.0);
  gsl_matrix_set (m, 1, 1, -mu*(y[0]*y[0] - 1.0));
  dfdt[0] = 0.0;
  dfdt[1] = 0.0;
  return GSL_SUCCESS;
}

int
main (void)
{
  double mu = 10;
  gsl_odeiv2_system sys = {func, jac, 2, &mu};

  gsl_odeiv2_driver * d = 
    gsl_odeiv2_driver_alloc_y_new (&sys, gsl_odeiv2_step_rk8pd,
				  1e-6, 1e-6, 0.0);
  int i;
  double t = 0.0, t1 = 100.0;
  double y[2] = { 1.0, 0.0 };

  for (i = 1; i <= 100; i++)
    {
      double ti = i * t1 / 100.0;
      int status = gsl_odeiv2_driver_apply (d, &t, ti, y);

      if (status != GSL_SUCCESS)
	{
	  printf ("error, return value=%d\n", status);
	  break;
	}

      printf ("%.5e %.5e %.5e\n", t, y[0], y[1]);
    }

  gsl_odeiv2_driver_free (d);
  return 0;
}

O usuário pode trabalhar com funções de baixo nível diretamente, como nos seguinte exemplo. Nesse caso um resultado intermediário é mostrado após cada degrau dado com sucesso ao invés de a cada ponto de tempo equidistante.

int
main (void)
{
  const gsl_odeiv2_step_type * T 
    = gsl_odeiv2_step_rk8pd;

  gsl_odeiv2_step * s 
    = gsl_odeiv2_step_alloc (T, 2);
  gsl_odeiv2_control * c 
    = gsl_odeiv2_control_y_new (1e-6, 0.0);
  gsl_odeiv2_evolve * e 
    = gsl_odeiv2_evolve_alloc (2);

  double mu = 10;
  gsl_odeiv2_system sys = {func, jac, 2, &mu};

  double t = 0.0, t1 = 100.0;
  double h = 1e-6;
  double y[2] = { 1.0, 0.0 };

  while (t < t1)
    {
      int status = gsl_odeiv2_evolve_apply (e, c, s,
                                           &sys, 
                                           &t, t1,
                                           &h, y);

      if (status != GSL_SUCCESS)
          break;

      printf ("%.5e %.5e %.5e\n", t, y[0], y[1]);
    }

  gsl_odeiv2_evolve_free (e);
  gsl_odeiv2_control_free (c);
  gsl_odeiv2_step_free (s);
  return 0;
}

Para funções com multiplos parâmetros, a informação apropriada pode ser informada por meio do argumento params na definição de gsl_odeiv2_system (mu nesse exemplo) usando um apontador para uma estrutura.

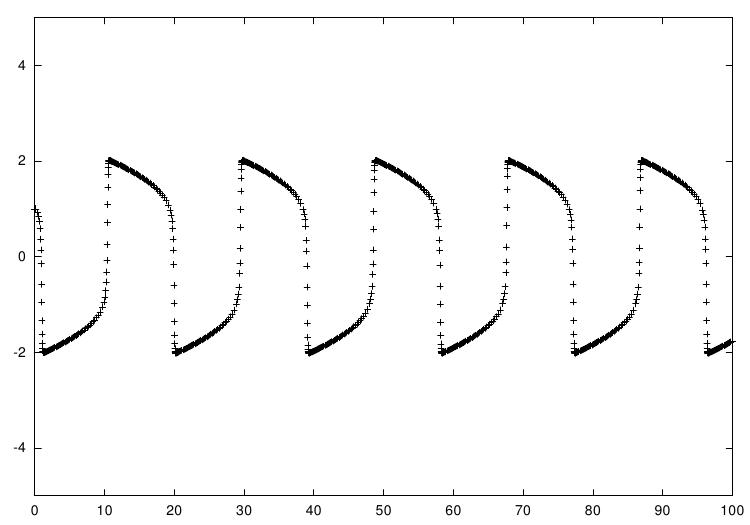
Solução numérica da equação do oscilador de Van der Pol usando o Runge-Kutta de oitava ordem de Prince-Dormand.

Também é possível trabalhar com um integrador não adaptativo, usando somente a função degrau propriamente dita, gsl_odeiv2_driver_apply_fixed_step ou gsl_odeiv2_evolve_apply_fixed_step. O seguinte programa usa a função de nível norteador, com função degrau de quarta ordem de Runge-Kutta com um tamanho de degrau fixo de 0.001.

int
main (void)
{
  double mu = 10;
  gsl_odeiv2_system sys = { func, jac, 2, &mu };

  gsl_odeiv2_driver *d =
    gsl_odeiv2_driver_alloc_y_new (&sys, gsl_odeiv2_step_rk4,
                                   1e-3, 1e-8, 1e-8);

  double t = 0.0;
  double y[2] = { 1.0, 0.0 };
  int i, s;

  for (i = 0; i < 100; i++)
    {
      s = gsl_odeiv2_driver_apply_fixed_step (d, &t, 1e-3, 1000, y);

      if (s != GSL_SUCCESS)
        {
          printf ("error: driver returned %d\n", s);
          break;
        }

      printf ("%.5e %.5e %.5e\n", t, y[0], y[1]);
    }

  gsl_odeiv2_driver_free (d);
  return s;
}

26.7 Referências e Leituras Adicionais

Ascher, U.M., Petzold, L.R., Computer Methods for Ordinary Differential and Differential-Algebraic Equations, SIAM, Philadelphia, 1998.

Hairer, E., Norsett, S. P., Wanner, G., Solving Ordinary Differential Equations I: Nonstiff Problems, Springer, Berlin, 1993.

Hairer, E., Wanner, G., Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, Springer, Berlin, 1996.

Muito das fórmulas básicas de Runge-Kutta pode ser encontrado no Handbook of Mathematical Functions,

Abramowitz & Stegun (eds.), Handbook of Mathematical Functions, Section 25.5.

O algoritmo implícito de Bulirsch-Stoer bsimp é descrito no seguinte artigo,

G. Bader and P. Deuflhard, “A Semi-Implicit Mid-Point Rule for Stiff Systems of Equações Diferenciais Ordinárias.”, Numer. Math. 41, 373–398, 1983.

Os métodos de degrau múltiplo de Adams e BDF msadams e msbdf são baseados nos seguintes artigos,

G. D. Byrne and A. C. Hindmarsh, “A Polyalgorithm for the Numerical Solution of Equações Diferenciais Ordinárias.”, ACM Trans. Math. Software, 1, 71–96, 1975.
P. N. Brown, G. D. Byrne and A. C. Hindmarsh, “VODE: A Variable-coefficient ODE Solver.”, SIAM J. Sci. Stat. Comput. 10, 1038–1051, 1989.
A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker and C. S. Woodward, “SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers.”, ACM Trans. Math. Software 31, 363–396, 2005.

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.