| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse capítulo descreve funções para executar interpolações. A biblioteca fornece uma variedade de métodos de interpolação, incluindo splines cúbicas e splines de Akima. Os tipos de interpolação são intercambiáveis, permitindo que diferentes métodos sejam usados sem a necessidade de recompilação. Interpolações podem ser definidas para ambas as condições de limite normal e periódica. Funções adicionais estão disponíveis para cálculo de derivadas e integrais de funções de interpolação.
Esses métodos de interpolação produzem curvas que passam através de cada ponto de dado. Para interpolar dados de ruído com uma curva plana veja Base Spline.
As funções descritas nessa seção são declaradas nos arquivos de cabeçalho ‘gsl_interp.h’ e ‘gsl_spline.h’.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Dados um conjunto de pontos de dados (x_1, y_1) \dots (x_n, y_n) as rotinas descritas nessa seção calculam uma função de interpolação contínua y(x) tal que y(x_i) = y_i. A interpolação é plana e definida por subfunções, e seu comportamento nas extremidade é determinado pelo tipo de interpolação usado.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
A função de interpolação para um certo conjunto de dados é armazenada em um
objeto gsl_interp. Esses objetos são criados pelas seguintes funções.
Essa função retorna um apontador para um recentemente alocado objeto de interpolação do tipo T para a quantidade size de pontos de dados.
Essa função inicializa o objeto de interpolação interp para os
dados (xa,ya) onde xa e ya são vetores estáticos de tamanho
size. O objeto de interpolação (gsl_interp) não grava
os vetores estáticos dos dados xa e ya e somente armazena o estado estático
calculado a partir dos dados. O vetor estático dos dados xa é sempre assumido ser
estritamente ordenado, com incremento dos valores de x;
o comportamento de outras disposições de elementos que não a estrita ordenação não está definida.
Essa função libera o objeto de interpolação interp.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
A biblioteca de interpolação fornece seis tipos de interpolação:
Interpolação linear. Esse método de interpolação não requer qualquer memória adicional.
Interpolação polinomial. Esse método deve somente ser usado para interpolar pequenos números de pontos pelo fato de a interpolação polinomial introduzir grandes oscilações, mesmo para conjuntos de pontos bem comportados. O número de termos na interpolação polinomial é igual ao número de pontos.
Spline cúbica com condições de limites naturais. A curva resultante é cúbica definida em partes sobre cada intervalo, com a primeira e a segunda derivada coincidindo nos pontos de dados fornecidos. A segunda derivada é escolhida para ser zero no primeiro ponto e no último ponto.
Spline cúbica com condições de limite periódicas. A curva resultante é cúbica definida por partes sobre cada intervalo, com a primeira e a segunda derivada coincidindo nos pontos de dados fornecidos. As derivadas no primeiro e últimos pontos são também coincidentes. Note que o último ponto nos dados devem ter o mesmo valor de y como o primeiro ponto, de outra forma a interpolação periódica resultante irá ter uma discontinuidade no limite.
Spline sem arredondamento de Akima com condições de limite natural. Esse método usa o algoritmo de canto sem arredondamento de Wodicka.
Spline sem arredondamento de Akima com condições de limite periódico. Esse método usa o algoritmo de canto sem arredondamento de Wodicka.
As seguintes funções relacionadas estão disponíveis:
Essa função retorna o nome do tipo de interpolação usada por interp. Por exemplo,
printf ("interp está usando a interpolação '%s'.\n",
gsl_interp_name (interp));
poderá imprimir algo como,
interp está usando a interpolação 'cspline'.
Essas funções retornam o menor número de pontos necessários ao objeto de interpolação interp ou ou necessário ao tipo de interpolação T. Por exemplo, a interpolação spline de Akima requer um mínimo de 5 pontos.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O estado de buscas pode ser armazenado em um objeto gsl_interp_accel,
que é um tipo de iterador para pesquisas de interpolação. Guarda na memória de acesso rápido os
valores anteriores de uma pesquisa de índice. Quando ponto subsequente de interpolação
encontra-se no mesmo intervalo seu valor de índice pode ser retornado
imediatamente.
Essa função retorna o índice i do vetor estático x_array tal
que x_array[i] <= x < x_array[i+1]. O índice é buscado
no intervalo [index_lo,index_hi]. Uma versão modificada dessa função é usada quando HAVE_INLINE for definida.
Essa função retorna um apontador para um objeto acelerador, que é um tipo de iterador para pesquisas de interpolação. Rastreia o estado de pesquisas, dessa forma permitindo a aplicação de várias estratégias de aceleração.
Essa função executa uma ação de pesquisa no vetor estático de dados x_array
de tamanho size, usando o acelerador fornecido a. É através dessa função que
pesquisas são executadas durante avaliação de uma interpolação. A
função retorna um índice i tal que x_array[i] <= x <
x_array[i+1]. Uma versão modificada dessa função é usada quando HAVE_INLINE for definida.
Essa função reinicializa o objeto acelerador acc. Deve ser usada quando a informação colocada na memória de acesso rápido não for mais aplicável—por exemplo, quando muda para um novo conjunto de dados.
Essa função libera o objeto acelerador acc.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essas funções retornam o valor interpolado de y para um dado
ponto x, usando o objeto de interpolação interp, vetores estáticos de
dados xa e ya e o acelerador acc. Quando
x estiver fora do intervalo de xa, o código de erro
GSL_EDOM é retornado com um valor de GSL_NAN para
y.
Essas funções retornam a derivada d de uma função interpolada para um dado ponto x, usando o objeto de interpolação interp, vetores estáticos de dados xa e ya e o acelerador acc.
Essas funções retornam a segunda derivada d2 de uma função interpolada para um dado ponto x, usando o bjeto de interpolação interp, vetores de dados xa e ya e o acelerador acc.
Essas funções retornam a integral numérica result de uma função interpolada sobre o intervalo [a, b], usando o objeto de interpolação interp, vetores estáticos de dados xa e ya e o acelerador acc.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
As funções descritas nas seções anteriores requerem que o usuário
forneça apontadores para os vetores estáticos x e y a cada chamada. As
seguintes funções são equivalentes às correspondentes
funções gsl_interp mas preservam uma cópias desses dados no
objeto gsl_spline. Essa preservação remove a necessidade de informar ambos xa
e ya como argumentos a cada avalliação. Essas funções são
definidas no arquivo de cabeçalho ‘gsl_spline.h’.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
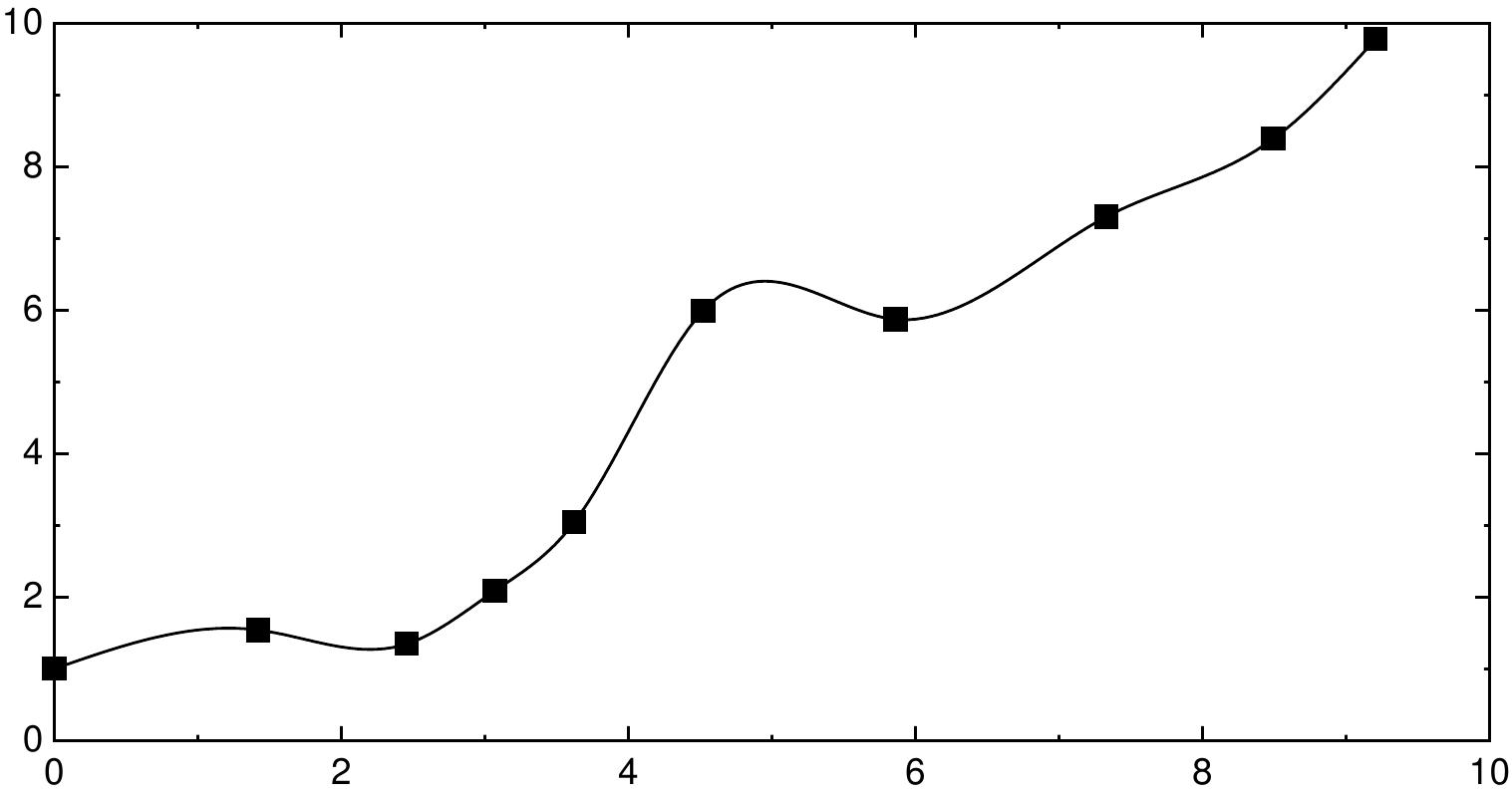
O seguinte programa demonstra o uso de funções de interpolação e de spline. O programa calcula uma interpolação spline cúbica do conjunto de dados de 10 pontos (x_i, y_i) onde x_i = i + \sin(i)/2 e y_i = i + \cos(i^2) para i = 0 \dots 9.
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_spline.h>
int
main (void)
{
int i;
double xi, yi, x[10], y[10];
printf ("#m=0,S=2\n");
for (i = 0; i < 10; i++)
{
x[i] = i + 0.5 * sin (i);
y[i] = i + cos (i * i);
printf ("%g %g\n", x[i], y[i]);
}
printf ("#m=1,S=0\n");
{
gsl_interp_accel *acc
= gsl_interp_accel_alloc ();
gsl_spline *spline
= gsl_spline_alloc (gsl_interp_cspline, 10);
gsl_spline_init (spline, x, y, 10);
for (xi = x[0]; xi < x[9]; xi += 0.01)
{
yi = gsl_spline_eval (spline, xi, acc);
printf ("%g %g\n", xi, yi);
}
gsl_spline_free (spline);
gsl_interp_accel_free (acc);
}
return 0;
}
A saída foi pensada de forma a poder ser usada com o programa graph
contido no pacote GNU plotutils,
$ ./a.out > interp.dat $ graph -T ps < interp.dat > interp.ps

O resultado mostra uma interpolação plana dos pontos originais. O
método de interpolação pode ser modificado simplesmente variando o primeiro argumento de
gsl_spline_alloc.
O seguinte programa demonstra uma spline periódica cúbica com 4 pontos de dados. Note que o primeiro e o último pontos devem ser fornecidos com o mesmo valor de y para uma spline periódica.
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_spline.h>
int
main (void)
{
int N = 4;
double x[4] = {0.00, 0.10, 0.27, 0.30};
double y[4] = {0.15, 0.70, -0.10, 0.15};
/* Note: y[0] == y[3] for periodic data */
gsl_interp_accel *acc = gsl_interp_accel_alloc ();
const gsl_interp_type *t = gsl_interp_cspline_periodic;
gsl_spline *spline = gsl_spline_alloc (t, N);
int i; double xi, yi;
printf ("#m=0,S=5\n");
for (i = 0; i < N; i++)
{
printf ("%g %g\n", x[i], y[i]);
}
printf ("#m=1,S=0\n");
gsl_spline_init (spline, x, y, N);
for (i = 0; i <= 100; i++)
{
xi = (1 - i / 100.0) * x[0] + (i / 100.0) * x[N-1];
yi = gsl_spline_eval (spline, xi, acc);
printf ("%g %g\n", xi, yi);
}
gsl_spline_free (spline);
gsl_interp_accel_free (acc);
return 0;
}
A saída pode ser mostrada com o GNU graph.
$ ./a.out > interp.dat $ graph -T ps < interp.dat > interp.ps
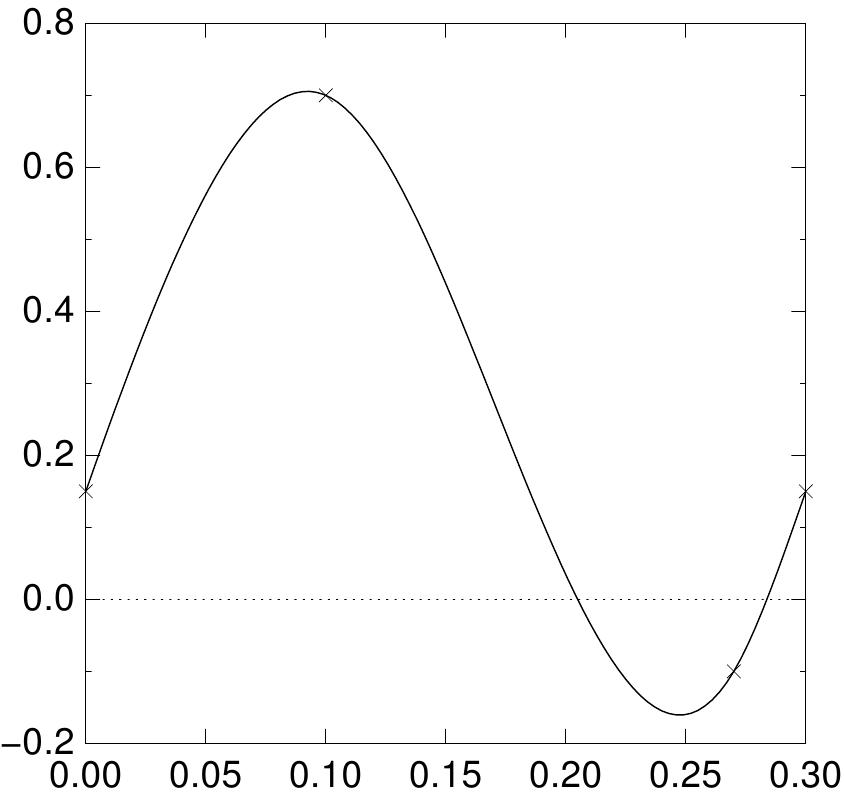
O resultado mostra uma interpolação periódica dos pontos originais. A inclinação da curva ajustada é a mesma no início e no final dos dados, e a segunda derivada também.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Descrições dos algoritmos de interpolação e referências adicionais podem ser encontradas nos seguintes livros:
| [ << ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.