| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse capítulo descreve funções para o cálculo de suavisação de splines base (B-splines). Um spline suavisada difere de um spline interpolada na curva resultante onde não é requerido que a mesma passe através de cada ponto de dados. Veja Veja seção Interpolação, para informação sobre interpolação de splines.
O arquivo de cabeçalho ‘gsl_bspline.h’ contém os protótipos para as funções bspline e declarações relacionadas.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
B-splines são comumente usadas como funções base para ajustar curvas
planas para grandes conjuntos de dados. Para fazer isso, o eixo das abscissas é
quebrado em algum número de intervalos, onde as extremidades
de cada intervalo são chamadas pontos de parada. Esses pontos de parada
são então convertidos para nós impondo-se várias condições de
continuidade e suavisação em cada interface. Dado um não decrescente
vetor de nós
t = {t_0, t_1, …, t_{n+k-1}},
as n splines base de ordem k são definidas por
|
|
Se definirmos nós apropriados sobre um intervalo [a,b] então
as funções B-spline base formam um completo conjunto sobre aquele intervalo.
Todavia podemos expandir uma função de suavisação como
|
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O cálculo de funções B-spline requerem um pré-alocado
espaço de trabalho do tipo gsl_bspline_workspace. Se derivadas
de B-spline forem também requeridas, um adicional
é necessário gsl_bspline_deriv_workspace.
Essa função aloca um espaço de trabalho para calcular B-splines de ordem k. O número de pontos de parada é dado por nbreak. Isso conduz a n = nbreak + k - 2 funções base. B-splines cúbicas são especificadas por k = 4. O tamanho do espaço de trabalho é O(5k + nbreak).
Essa função libera a memória associada ao espaço de trabalho w.
Essa função aloca um espaço de trabalho para calcular as derivadas de uma função B-spline base de ordem k. O tamanho do espaço de trabalho é O(2k^2).
Essa função libera a memória associada ao espaço de trabalho de derivadas w.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função calcula os nós associados aos dados pontos de parada
e armazena-os internamente em w->knots.
Essa função assume pontos de parada uniformemente espaçados no intervalo [a,b]
e constrói o correspondente vetor de nós usando o préviamente
especificado parâmetro nbreak. Os nós são armazenados em
w->knots.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função avalia todas funções B-spline base na posição
x e armazena-as no vetor B, de forma que o i-ésimo elemento
é B_i(x). O vetor B deve ser de comprimento
n = nbreak + k - 2. Esse valor pode também ser obtido chamando
gsl_bspline_ncoeffs.
Calculando todas as funções de base uma única vez é mais eficiente que
calculá-las individualmente, devido à natureza de definir
relações de recorrência.
Essa função avalia todos potencialmente não nulas funções B-spline base na posição x e armazena-as em um vetor Bk, de forma que o i-ésimo elemento seja B_(istart+i)(x). O último elemento de Bk é B_(iend)(x). O vetor Bk deve ser de comprimento k. Por meio do retorno de somente funções de base não nulas, essa função permite que quantidades envolvendo combinações lineares de B_i(x) sejam calculadas sem termos desnecessários (tal combinação linear ocorre, por exemplo, quando avalia-se uma função interpolada).
Essa função retorna o número de coeficientes de B-spline dado por n = nbreak + k - 2.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Essa função avalia todas as derivadas de funções B-spline base de ordem
0 até a ordem nderiv (inclusive) na posição x
e armazena-as na matriz dB. O (i,j)-ésimo elemento de dB
é d^jB_i(x)/dx^j. A matriz dB deve ser
de tamanho n = nbreak + k - 2 por nderiv + 1.
O valor n pode também ser obtida
chamando gsl_bspline_ncoeffs. Note que funções de avaliações
são incluídas como a derivada de zero-ésima ordem em dB.
calculando todas as derivadas de função base de uma vez é mais eficiente
que calculá-las individualmente, devido à natureza da definição da
relação de recorrência.
Essa função avalia todas as potencialmente não nulas derivadas de funções B-spline base de ordem 0 até a ordem nderiv (inclusive) na posição x e armazena-as na matriz dB. O (i,j)-ésimo elemento de dB é d^j/dx^j B_(istart+i)(x). A última linha de dB contém d^j/dx^j B_(iend)(x). A matriz dB deve ser de tamanho k o qual deve ser pelo menos nderiv + 1. Note que avaliações de função são incluídas como derivadas de zero-ésima ordem em dB. Por meio do retorno somente as funções base não nulas, essa função permite que quantidades envolvendo combinações lineares dos B_i(x) com suas derivadas sejam calculadas sem termos desnecessários.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
As abscissas de Greville são definidas para serem a localização média de k-1
nós consecutivos no vetor de nós para cada função spline base de ordem
k. Com o primeiro e últimos nós no vetor de nós no
gsl_bspline_workspace excluídos, existem gsl_bspline_ncoeffs abscissas de Greville
para qualquer dado B-spline base. Esses valores são muitas vezes usados em aplicações de
colocação de B-spline e pode também serem chamados pontos de Marsden-Schoenberg.
Retorna a localização da i-ésima abscissa de Greville para a dada B-spline base. Para o pior caso sendo k=1, a implementação escolhe retornar o ponto médio entre dois pontos de parada.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
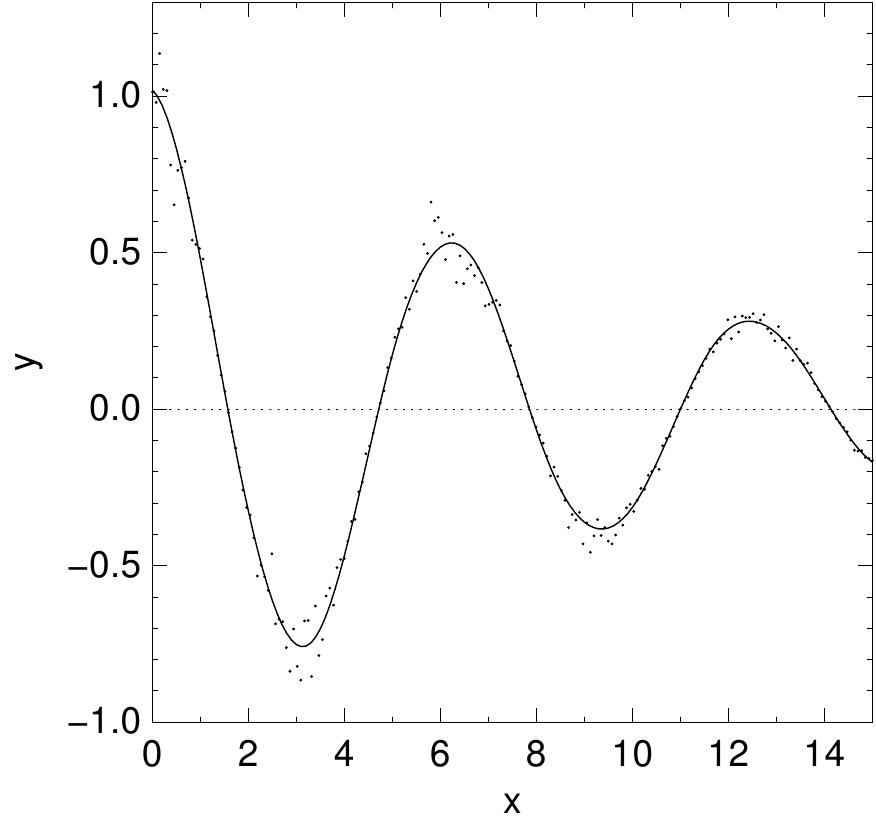
O seguinte programa calcula um ajuste linear por mínimos quadrados para dados usando funções de B-splines base cúbicas com pontos de parada uniforme. Os dados são gerados a partir da curva y(x) = \cos{(x)} \exp{(-x/10)} sobre o intervalo [0, 15] com ruído de Gauss adicionado.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <gsl/gsl_bspline.h>
#include <gsl/gsl_multifit.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
#include <gsl/gsl_statistics.h>
/* number of data points to fit */
#define N 200
/* number of fit coefficients */
#define NCOEFFS 12
/* nbreak = ncoeffs + 2 - k = ncoeffs - 2 since k = 4 */
#define NBREAK (NCOEFFS - 2)
int
main (void)
{
const size_t n = N;
const size_t ncoeffs = NCOEFFS;
const size_t nbreak = NBREAK;
size_t i, j;
gsl_bspline_workspace *bw;
gsl_vector *B;
double dy;
gsl_rng *r;
gsl_vector *c, *w;
gsl_vector *x, *y;
gsl_matrix *X, *cov;
gsl_multifit_linear_workspace *mw;
double chisq, Rsq, dof, tss;
gsl_rng_env_setup();
r = gsl_rng_alloc(gsl_rng_default);
/* allocate a cubic bspline workspace (k = 4) */
bw = gsl_bspline_alloc(4, nbreak);
B = gsl_vector_alloc(ncoeffs);
x = gsl_vector_alloc(n);
y = gsl_vector_alloc(n);
X = gsl_matrix_alloc(n, ncoeffs);
c = gsl_vector_alloc(ncoeffs);
w = gsl_vector_alloc(n);
cov = gsl_matrix_alloc(ncoeffs, ncoeffs);
mw = gsl_multifit_linear_alloc(n, ncoeffs);
printf("#m=0,S=0\n");
/* this is the data to be fitted */
for (i = 0; i < n; ++i)
{
double sigma;
double xi = (15.0 / (N - 1)) * i;
double yi = cos(xi) * exp(-0.1 * xi);
sigma = 0.1 * yi;
dy = gsl_ran_gaussian(r, sigma);
yi += dy;
gsl_vector_set(x, i, xi);
gsl_vector_set(y, i, yi);
gsl_vector_set(w, i, 1.0 / (sigma * sigma));
printf("%f %f\n", xi, yi);
}
/* use uniform breakpoints on [0, 15] */
gsl_bspline_knots_uniform(0.0, 15.0, bw);
/* construct the fit matrix X */
for (i = 0; i < n; ++i)
{
double xi = gsl_vector_get(x, i);
/* compute B_j(xi) for all j */
gsl_bspline_eval(xi, B, bw);
/* fill in row i of X */
for (j = 0; j < ncoeffs; ++j)
{
double Bj = gsl_vector_get(B, j);
gsl_matrix_set(X, i, j, Bj);
}
}
/* do the fit */
gsl_multifit_wlinear(X, w, y, c, cov, &chisq, mw);
dof = n - ncoeffs;
tss = gsl_stats_wtss(w->data, 1, y->data, 1, y->size);
Rsq = 1.0 - chisq / tss;
fprintf(stderr, "chisq/dof = %e, Rsq = %f\n",
chisq / dof, Rsq);
/* output the smoothed curve */
{
double xi, yi, yerr;
printf("#m=1,S=0\n");
for (xi = 0.0; xi < 15.0; xi += 0.1)
{
gsl_bspline_eval(xi, B, bw);
gsl_multifit_linear_est(B, c, cov, &yi, &yerr);
printf("%f %f\n", xi, yi);
}
}
gsl_rng_free(r);
gsl_bspline_free(bw);
gsl_vector_free(B);
gsl_vector_free(x);
gsl_vector_free(y);
gsl_matrix_free(X);
gsl_vector_free(c);
gsl_vector_free(w);
gsl_matrix_free(cov);
gsl_multifit_linear_free(mw);
return 0;
} /* main() */
A saída pode ser mostrada com o GNU graph.
$ ./a.out > bspline.dat chisq/dof = 1.118217e+00, Rsq = 0.989771 $ graph -T ps -X x -Y y -x 0 15 -y -1 1.3 < bspline.dat > bspline.ps

| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Informação adicional sobre os algoritmos descritos nessa seção pode ser encontrado no seguinte livro,
Informação adicional sobre as abscissas de Greville e colocação de B-spline pode ser encontrado no seguinte artigo,
Uma grande coleção de rotinas B-spline está disponivel na biblioteca PPPACK disponível em http://www.netlib.org/pppack, que é também parte de SLATEC.
| [ << ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.