38 Ajuste por Mínimos Quadrados Não Linear

Esse capitulo descreve funções para ajuste por mínimos quadrados não linear multidimensional. A biblioteca fornece componentes de baixo nível para uma variedade de resolvedores iterativos e testes de convergência. Esses resolvedores e testes podem ser combinados pelo usuário para encontrar a solução desejada, com acesso completo aos passos intermediários da iteração. Cada classe de métodos usa a mesma estrutura, de forma que você poe alternar entre resolvedores durante a execução sem precisar recompilar seu programa. Cada instância de um resolvedor mantém registros de seu próprio estado, permitindo aos reoslvedores serem usados em programas com suporte a multiplas linhas de execução.

O arquivo de cabeçalho ‘gsl_multifit_nlin.h’ contém protótipos para funções de ajuste não linear multidimensional e declarações relacionadas.

38.1 Visão Geral

O problema de ajuste por mínimos quadrados não linear multidimensional requer a minimização dos residuais quadrados de n funções, f_i, em p parâmetros, x_i,

Φ(x) =

|| F(x) ||² =

n
∑
i=1

f_i (x₁, ..., x_p)²

Todos os algoritmos procedem a partir de uma suposição inicial usando a linearização,

ψ(p) = || F(x+p) || ≈ || F(x) + J p ||

onde x é o ponto inicial, p é o passo proposto e J é a matriz de Jacobi J_{ij} = d f_i / d x_j. estratégias adicionais são usadas para ampliar a região de convergência. Isso inclui requerer um decrescimento do módulo ||F|| a cada passo ou usando uma região confiável para evitar passo que caem fora do regime linear.

Para executar um ajuste por mínimos quadrados ponderado de um modelo não linear Y(x,t) para dados (t_i, y_i) com erros de Gauss independentes \sigma_i, use componentes de função da seguinte forma,

f_i =

(Y(x, t_i) − y_i)

σ_i

Note que os parâmetros de modelo são denotados por x nesse capítulo uma vez que algoritmos por mínimos quadrados não lineares são descritos geometricamente (i.e. encontrando o mínimo de uma superfície). A variável independente de quaisquer dados a ser ajustado é denotado por t.

Com a definição acima a matriz de Jacobi é J_{ij} =(1 / \sigma_i) d Y_i / d x_j, onde Y_i = Y(x,t_i).

38.2 Inicializando o Resolvedor

Function: gsl_multifit_fsolver * gsl_multifit_fsolver_alloc (const gsl_multifit_fsolver_type * T, size_t n, size_t p)

Essa função retorna um apontador para uma recentemente alocada instância de um resolvedor do tipo T para n observações e p parâmetros. O número de observações n deve ser maior que ou igual a p parâmetros.

Se não houver memória suficiente para criar o resolvedor então a função retorna um apontador nulo e o controlador de erro é chamdo com um código de erro de GSL_ENOMEM.

Function: gsl_multifit_fdfsolver * gsl_multifit_fdfsolver_alloc (const gsl_multifit_fdfsolver_type * T, size_t n, size_t p)

Essa função retorna um apontador par uma recentemente alocada instância de um resolvedor derivativo do tipo T para n observações e p parametros. Por exemplo, o seguinte código cria uma instância de um resolvedor de Levenberg-Marquardt para 100 pontos de dados e 3 parâmetros,

const gsl_multifit_fdfsolver_type * T 
    = gsl_multifit_fdfsolver_lmder;
gsl_multifit_fdfsolver * s 
    = gsl_multifit_fdfsolver_alloc (T, 100, 3);

O número de observaçõe n deve ser maior que ou igual a parâmetros p.

Se houver memória insuficiente para criar o resolvedor então a função retorna um apontador nulo e o controlador de erro é chamado com um código de erro de GSL_ENOMEM.

Function: int gsl_multifit_fsolver_set (gsl_multifit_fsolver * s, gsl_multifit_function * f, const gsl_vector * x): Essa função inicializa, ou reinicializa, um resolvedor existente s para usar a função f e a suposição inicial x.

Function: int gsl_multifit_fdfsolver_set (gsl_multifit_fdfsolver * s, gsl_multifit_function_fdf * fdf, const gsl_vector * x): Essa função inicializa, ou reinicaliza, um resolvedor existente s para usar a função e derivada fdf e a suposição inicial x.

Function: void gsl_multifit_fsolver_free (gsl_multifit_fsolver * s)
Function: void gsl_multifit_fdfsolver_free (gsl_multifit_fdfsolver * s): Essas funções liberam toda a memória associada ao resolvedor s.

Function: const char * gsl_multifit_fsolver_name (const gsl_multifit_fsolver * s)

Function: const char * gsl_multifit_fdfsolver_name (const gsl_multifit_fdfsolver * s)

Essas funções retornam um apontador para o nome do resolvedor. Por exemplo,

printf ("s é um resolvedor '%s'\n", 
        gsl_multifit_fdfsolver_name (s));

pode imprimir alguma coisa como s é um resolvedor 'lmder'.

38.3 Fornecendo a Função a ser Minimizada

Você deve fornecer n funções de p variáveis para os algoritmos de minimização trabalhar sobre elas. Com o objetivo de permitir parâmetros arbitrários as funções são definidas pelos seguintes tipos de dado:

Data Type: gsl_multifit_function

Esse tipo de dado define um sistema geral de funções com parâmetros arbitrários.

int (* f) (const gsl_vector * x, void * params, gsl_vector * f): essa função deve armazenar o vetor resultado f(x,params) em f para argumento x e parâmetros arbitrários params, retornando um código de erro apropriado se a função não puder ser calculada.
size_t n: o número de funções, i.e. o número de componentes do vetor f.
size_t p: o número de variáveis independentes, i.e. o número de componenetes do vetor x.
void * params: um apontador para os parâmetros arbitrários da função.

Data Type: gsl_multifit_function_fdf

Esse tipo de dado define um sistema geral de funções com parâmetros arbitrários e a correspondente matriz de Jacobi de derivadas,

int (* f) (const gsl_vector * x, void * params, gsl_vector * f): essa função deve armazenar o vetor resultado f(x,params) em f para o argumento x e parâmetros arbitrários params, retornando uma código de erro apropriado se a função não puder ser calculada.
int (* df) (const gsl_vector * x, void * params, gsl_matrix * J): essa função deve armazenar a matriz resultado n-por-p J_ij = d f_i(x,params) / d x_j em J para argumento x e parâmetros arbitrários params, retornando um código de erro apropriado se a função não puder ser calculada. Se um Jacobiano analítico não estiver disponível, ou for muito dispendioso fazer o sálculo desse jacobiano analítico, esse apontador de função pode ser sjuatado para NULL, nesse caso o Jacobiano irá ser calculad internamente usando aproximação por diferenças finitas da função f.
int (* fdf) (const gsl_vector * x, void * params, gsl_vector * f, gsl_matrix * J): Essa função deve ajustar os valores de f e J como acima, para argumentos x e parâmetros arbitrários params. Essa função fornece uma otimização de funções separadas para f(x) e J(x)—é sempre mais rápido calcular a função e sua derivada ao mesmo tempo. If an analytic Jacobian is unavailable, or too expensive to compute, this function pointer may be set to NULL, in which case the Jacobian will be internally computed using finite difference approximations of the function f.
size_t n: o número de funções, i.e. o número de componenetes do vetor f.
size_t p: o número de varáveis independentes, i.e. o número de componentes do vetor x.
void * params: um apontador para os parâmetros arbitrários da função.

Note que quando ajustando um modelo não linear contra dados experimentais, os dados são informados para as funções acima usando o argumento params e os melhores parâmetros de teste através do argumento x.

38.4 Diferenças Finitas Jacobianas

Para os algorítmos que requerem uma matriz de Jacobi de derivadas das funções de ajuste, existem ocasiões onde um analítico de Jacobi encontra-se indisponível ou pode ser muito dispendioso calcular. Apesar disso a GSL suporta aproximações do Jacobiano numericamente usando diferenças finitas das funções de ajuste. Essa aproximação é tipicamente feita ajustando os apontadores de função relevantes do tipo gsl_multifit_function_fdf para NULL, todavia as seguintes funções permitem ao usuário acessar a aproximação do Jacobiano diretamente se precisar.

Function: int gsl_multifit_fdfsolver_dif_df (const gsl_vector * x, gsl_multifit_function_fdf * fdf, const gsl_vector * f, gsl_matrix * J): Essa função toma como entrada a posição atual x com com os valores de função calculados na posição atual f, de acordo com fdf que especifica a função de ajuste e os parâmetros e aproxima o Jacobiano J de ordem n-por-p usando diferenças finitas adiante: J_ij = d f_i(x,params) / d x_j = (f_i(x^*,params) - f_i(x,params)) / d x_j. onde x^* tem o j-ésimo elemento perturbado por \Delta x_j e \Delta x_j = \epsilon |x_j|, onde \epsilon é a raíz quadrada da precisão de máquina GSL_DBL_EPSILON.

Function: int gsl_multifit_fdfsolver_dif_fdf (const gsl_vector * x, gsl_multifit_function_fdf * fdf, gsl_vector * f, gsl_matrix * J): Essa função calcula o vetor de valores de função f e o Jacobiano aproximado J no vetor posição x usando o sistema descrito em fdf. Veja gsl_multifit_fdfsolver_dif_df para uma descrição de como o Jacobiano é calculado.

38.5 Iteração

As seguintes funções norteiam a iteração de cada algoritmo. Cada função executa uma iteração para atualizar o estado de qualquer resolvedor do tipo correspondente. A mesma função trabalha para todos os resolvedores de forma que diferentes métodos podem ser substituídos durante a execução sem modificações no código.

Function: int gsl_multifit_fsolver_iterate (gsl_multifit_fsolver * s)
Function: int gsl_multifit_fdfsolver_iterate (gsl_multifit_fdfsolver * s): Essas funções executam uma iteração simples do resolvedor s. Se a iteração encontrar um problema inesperado então um código de erro irá ser retornado. O resolvedor mantém uma estimativa atual dos parâmetros de melhor ajuste em todas as vezes.

A estrutura do resolvedor s contém as seguintes entradas, que podem ser usadas para registrar o progresso das soluções:

gsl_vector * x: A posição atual.
gsl_vector * f: O valor de função na posição atual.
gsl_vector * dx: A diferença entre a posição atual e a posição anterior, i.e. o último passo, tomado como um vetor.
gsl_matrix * J: A matriz de Jacobi na posição atual (para a estrutura gsl_multifit_fdfsolver somente)

A informação de melhor ajuste também pode ser acessada com as seguintes funções auxiliares,

Function: gsl_vector * gsl_multifit_fsolver_position (const gsl_multifit_fsolver * s)
Function: gsl_vector * gsl_multifit_fdfsolver_position (const gsl_multifit_fdfsolver * s): Essas funções retornam a atual posição (i.e. parâmetros de melhor ajuste) s->x do resolvedor s.

38.6 Busca por Parâmetros de Parada

Um procedimento de minimização deve parar quando uma das seguintes condições for verdadeira:

Um mínimo foi encontrado dentro da precisão especificada pelo usuário.
Um número máximo de iterações foi alcançado.
Um erro ocorreu.

O manipulação dessas condições está sob o controle do usuário. As funções abaixo permitem ao usuário testar a atual estimativa de parâmetros de melhor ajuste de muitas formas padronizadas.

Function: int gsl_multifit_test_delta (const gsl_vector * dx, const gsl_vector * x, double epsabs, double epsrel)

Essa função testa para convergência da sequência comparando o último passo dx com o erro absoluto epsabs e erro relativo epsrel na atual posição x. O teste retorna GSL_SUCCESS se a seguinte condição for alcançada,

|dx_i| < epsabs + epsrel |x_i|

para cada componente de x e retorna GSL_CONTINUE de outra forma.

Function: int gsl_multifit_test_gradient (const gsl_vector * g, double epsabs)

Essa função testa o coeficiente angular residual g contra o limite de erro absoluto epsabs. Matematicamente, o coeficiente angular deve ser exatamente zero no mínimo. O teste retorna GSL_SUCCESS se a seguinte condição for alcançada,

∑
i

|g_i| < epsabs

e retorna GSL_CONTINUE de outra forma. Esse critério é adequado para situações onde a localização precisa do mínimo, x, é secundária uma vez que um valor pode ser encontrado onde o coeficiente angular é pequeno o suficiente.

Function: int gsl_multifit_gradient (const gsl_matrix * J, const gsl_vector * f, gsl_vector * g): Essa função calcula o coeficiente angular g de \Phi(x) = (1/2) ||F(x)||^2 a partir da matriz de Jacobi J e os valores da função f, usando a fórmula g = J^T f.

38.7 High Level Driver

Essas rotinas fornecem um invólucro de alto nível que combina iteração e teste de convergência para facilitar o uso em situações onde ambos sejam necessários.

Function: int gsl_multifit_fsolver_driver (gsl_multifit_fsolver * s, const size_t maxiter, const double epsabs, const double epsrel)
Function: int gsl_multifit_fdfsolver_driver (gsl_multifit_fdfsolver * s, const size_t maxiter, const double epsabs, const double epsrel): Essas funções fazem a iteração do resolvedor s para o máximo de maxiter iterações. Após cada iteração, o sistema é testado para converfência usando gsl_multifit_test_delta com tolerâncias de erro epsabs e epsrel.

38.8 Algoritmos de Minimização usando Derivada

Os algoritmos de minimização descritos nessa seção fazem uso de ambas a função e sua derivada. Os algoritmos requerem uma suposição incial para a localização do mínimo. Não existe garantias absolutas de convergência—a função deve ser adequada a essa técnica e a suposição inicial deve estar suficientemente perto do mínimo para que esse algoritmo funcione.

Derivative Solver: gsl_multifit_fdfsolver_lmsder

Essa é uma versão robusta e eficiente do algoritmo de Levenberg-Marquardt como implementado na rotina escalonada LMDER em MINPACK. Minpack foi escrito por Jorge J. Moré, Burton S. Garbow e Kenneth E. Hillstrom.

O algoritmo usa uma região de confiabilidade generalizada para manter cada passo sob controle. Com o objetivo de ser aceita uma nova posição proposta x' deve satisfazer a condição |D (x' - x)| < \delta, onde D é uma matriz escalonada diagonal e \delta é o tamanho da região de confiabilidade. As componentes de D são calculadas internamente, usando os módulos de coluna do determinate de Jacobi para estimar a sensibilidade do resíduo para cada componente de x. Isso melhora o comportamento do algoritmo para função péssimamente escalonadas.

A cada iteração o algoritmo tenta minimizar o sistema linear |F + J p| com relação à restrição |D p| < \Delta. A solução para esse sistema linear restrito é encontrada usando o método de Levenberg-Marquardt.

O passo proposto é agora testado avaliando a função no ponto resultante, x'. Se o passo reduzir o módulo da função suficientemente, e seguir o comportamento previsto da função dentro da região de confiabilidade, então é aceito e o tamanho da região de confiabilidade é aumentado. Se o passo proposto falha em melhorar a solução, ou difere significativamente do comportamento esperado dentro da região de confiabilidade, então o tamanho da região de confiabilidade é reduzido e outro passo de teste é calculado.

O algoritmo também monitora o progresso da solução e retorna um erro se as modificações na solução forem menores que a precisão da máquina. Os possíveis códigos de erro são,

GSL_ETOLF: a região de decrescimento na função cai abaixo da precisão da máquina
GSL_ETOLX: a modificação no vetor posição cai abaixo da precisão da máquina
GSL_ETOLG: o módulo do coeficiente angular, relativo ao módulo da função, cai abaixo da precisão da máquina
GSL_ENOPROG: a rotina fez 10 ou mais tentativas de encontrar um adequado passo de teste sem sucesso (mas subsequêntes chamadas podem ser fetas para continuar a busca).(75)

Esses códigos de erro indicam iterações adicionais terão pouca probabilidade de mudar a solução a partir de seu atual valor.

Derivative Solver: gsl_multifit_fdfsolver_lmder: Essa é uma versão não escalonada do algoritmo de LMDER. Os elementos da matriz escalonada diagonal D são ajustados para 1. Esse algoritmo pode ser útil em circunstâncias onde a versão escalonada de LMDER converge muito lentamente, ou a função já foi escalonada apropriadamente.

38.9 Algoritmos de Minimização sem Derivadas

Não existem algoritmos implementados nessa seção no presente momento.

38.10 Calculando a matriz de covariância de parâmetros de melhor ajuste

Function: int gsl_multifit_covar (const gsl_matrix * J, double epsrel, gsl_matrix * covar)

Essa função usa a matrix de Jacobi J para calcular a matrix de covariância dos parâmetros de melhor ajuste, covar. O parâmetro epsrel é usado para remover colunas linearmente dependentes quando J for posto deficiente.

A matriz de covariância é dada por,

C = (J^T J)⁻¹

e é calculada por decomposição QR de J com pivotamento por colunas. Quaisquer colunas de R que satisfizer

|R_kk| ≤ epsrel |R₁₁|

são consideradas linearmene dependentes e são excluídas da matriz de covariância (as correspondentes linhas e colunas da matriz de covariância são ajustadas para zero).

Se a redução ao mínimo usa a função de mínimos quadrados ponderados f_i = (Y(x, t_i) - y_i) / \sigma_i então a matrix de covariância acima fornece o erro estatístico sobre os parâmetros de melhor ajuste resultando de erros de Gauss \sigma_i sobre os dados básicos y_i. Isso pode ser verificado a partir da relação \delta f = J \delta c e o fato de que as flutuações em f a partir dos dados y_i são normalizadas por \sigma_i e então satisfazem <\delta f \delta f^T> = I.

Para uma função de mínimos quadrados não ponderada f_i = (Y(x, t_i) - y_i) a matriz de covariância acima deve ser multiplicada pela variância dos resíduos sobre o melhor ajuste \sigma^2 = \sum (y_i - Y(x,t_i))^2 / (n-p) para fornecer a matriz de variância-covariância \sigma^2 C. Isso estima o erro estatístico sobre os parâmetros de melhor ajuste da dispersão dos dados básicos.

Para mais informações sobre matrizes de covariância veja Visão Geral.

38.11 Exemplos

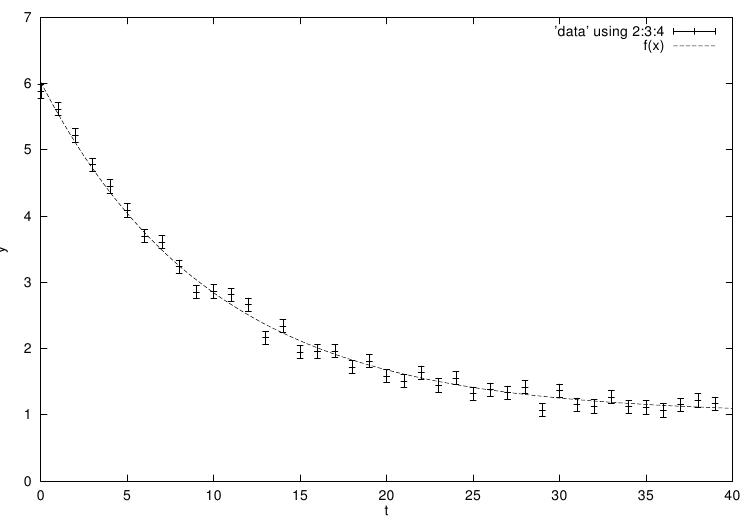
O seguinte programa exemplo ajusta um modelo exponencial ponderado como pano de fundo para dados experimentais, Y = A \exp(-\lambda t) + b. A primeira parte do programa ajusta as funções expb_f e expb_df para calcular o modelo e seu determinante de Jacobi. A apropriada função a ser ajustada é dada por,

f_i = ((A exp(−λt_i) + b) − y_i)/σ_i

onde escolhemos t_i = i. A matriz de Jacobi J é a derivada dessas funções com relação a três parâmetros (A, \lambda, b). é dada por,

J_ij =

∂f_i

∂x_j

onde x_0 = A, x_1 = \lambda e x_2 = b.

/* expfit.c -- model functions for exponential + background */

struct data {
  size_t n;
  double * y;
  double * sigma;
};

int
expb_f (const gsl_vector * x, void *data, 
        gsl_vector * f)
{
  size_t n = ((struct data *)data)->n;
  double *y = ((struct data *)data)->y;
  double *sigma = ((struct data *) data)->sigma;

  double A = gsl_vector_get (x, 0);
  double lambda = gsl_vector_get (x, 1);
  double b = gsl_vector_get (x, 2);

  size_t i;

  for (i = 0; i < n; i++)
    {
      /* Model Yi = A * exp(-lambda * i) + b */
      double t = i;
      double Yi = A * exp (-lambda * t) + b;
      gsl_vector_set (f, i, (Yi - y[i])/sigma[i]);
    }

  return GSL_SUCCESS;
}

int
expb_df (const gsl_vector * x, void *data, 
         gsl_matrix * J)
{
  size_t n = ((struct data *)data)->n;
  double *sigma = ((struct data *) data)->sigma;

  double A = gsl_vector_get (x, 0);
  double lambda = gsl_vector_get (x, 1);

  size_t i;

  for (i = 0; i < n; i++)
    {
      /* Jacobian matrix J(i,j) = dfi / dxj, */
      /* where fi = (Yi - yi)/sigma[i],      */
      /*       Yi = A * exp(-lambda * i) + b  */
      /* and the xj are the parameters (A,lambda,b) */
      double t = i;
      double s = sigma[i];
      double e = exp(-lambda * t);
      gsl_matrix_set (J, i, 0, e/s); 
      gsl_matrix_set (J, i, 1, -t * A * e/s);
      gsl_matrix_set (J, i, 2, 1/s);
    }
  return GSL_SUCCESS;
}

int
expb_fdf (const gsl_vector * x, void *data,
          gsl_vector * f, gsl_matrix * J)
{
  expb_f (x, data, f);
  expb_df (x, data, J);

  return GSL_SUCCESS;
}

A parte principal do programa ajusta um resolvedor Levenberg-Marquardt e alguns dados aleatórios simulados. Os dados usam os conhecidos parâmetros (1.0,5.0,0.1) combinados com ruídos de Gauss (desvio padrão = 0.1) sobre um intervalo de 40 intervalos de tempo. A suposição inicial para os parâmetros é escolhida como (0.0, 1.0, 0.0).

#include <stdlib.h>
#include <stdio.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_blas.h>
#include <gsl/gsl_multifit_nlin.h>

#include "expfit.c"

#define N 40

void print_state (size_t iter, gsl_multifit_fdfsolver * s);

int
main (void)
{
  const gsl_multifit_fdfsolver_type *T;
  gsl_multifit_fdfsolver *s;
  int status;
  unsigned int i, iter = 0;
  const size_t n = N;
  const size_t p = 3;

  gsl_matrix *covar = gsl_matrix_alloc (p, p);
  double y[N], sigma[N];
  struct data d = { n, y, sigma};
  gsl_multifit_function_fdf f;
  double x_init[3] = { 1.0, 0.0, 0.0 };
  gsl_vector_view x = gsl_vector_view_array (x_init, p);
  const gsl_rng_type * type;
  gsl_rng * r;

  gsl_rng_env_setup();

  type = gsl_rng_default;
  r = gsl_rng_alloc (type);

  f.f = &expb_f;
  f.df = &expb_df;
  f.fdf = &expb_fdf;
  f.n = n;
  f.p = p;
  f.params = &d;

  /* This is the data to be fitted */

  for (i = 0; i < n; i++)
    {
      double t = i;
      y[i] = 1.0 + 5 * exp (-0.1 * t) 
                 + gsl_ran_gaussian (r, 0.1);
      sigma[i] = 0.1;
      printf ("data: %u %g %g\n", i, y[i], sigma[i]);
    };

  T = gsl_multifit_fdfsolver_lmsder;
  s = gsl_multifit_fdfsolver_alloc (T, n, p);
  gsl_multifit_fdfsolver_set (s, &f, &x.vector);

  print_state (iter, s);

  do
    {
      iter++;
      status = gsl_multifit_fdfsolver_iterate (s);

      printf ("status = %s\n", gsl_strerror (status));

      print_state (iter, s);

      if (status)
        break;

      status = gsl_multifit_test_delta (s->dx, s->x,
                                        1e-4, 1e-4);
    }
  while (status == GSL_CONTINUE && iter < 500);

  gsl_multifit_covar (s->J, 0.0, covar);

#define FIT(i) gsl_vector_get(s->x, i)
#define ERR(i) sqrt(gsl_matrix_get(covar,i,i))

  { 
    double chi = gsl_blas_dnrm2(s->f);
    double dof = n - p;
    double c = GSL_MAX_DBL(1, chi / sqrt(dof)); 

    printf("chisq/dof = %g\n",  pow(chi, 2.0) / dof);

    printf ("A      = %.5f +/- %.5f\n", FIT(0), c*ERR(0));
    printf ("lambda = %.5f +/- %.5f\n", FIT(1), c*ERR(1));
    printf ("b      = %.5f +/- %.5f\n", FIT(2), c*ERR(2));
  }

  printf ("status = %s\n", gsl_strerror (status));

  gsl_multifit_fdfsolver_free (s);
  gsl_matrix_free (covar);
  gsl_rng_free (r);
  return 0;
}

void
print_state (size_t iter, gsl_multifit_fdfsolver * s)
{
  printf ("iter: %3u x = % 15.8f % 15.8f % 15.8f "
          "|f(x)| = %g\n",
          iter,
          gsl_vector_get (s->x, 0), 
          gsl_vector_get (s->x, 1),
          gsl_vector_get (s->x, 2), 
          gsl_blas_dnrm2 (s->f));
}

A iteração termina quando a modificação em x for menor que 0.0001, para ambas uma modificação absoluta e uma modificação relativa. Aqui está os resultados do programa executando:

iter: 0 x=1.00000000 0.00000000 0.00000000 |f(x)|=117.349
status=success
iter: 1 x=1.64659312 0.01814772 0.64659312 |f(x)|=76.4578
status=success
iter: 2 x=2.85876037 0.08092095 1.44796363 |f(x)|=37.6838
status=success
iter: 3 x=4.94899512 0.11942928 1.09457665 |f(x)|=9.58079
status=success
iter: 4 x=5.02175572 0.10287787 1.03388354 |f(x)|=5.63049
status=success
iter: 5 x=5.04520433 0.10405523 1.01941607 |f(x)|=5.44398
status=success
iter: 6 x=5.04535782 0.10404906 1.01924871 |f(x)|=5.44397
chisq/dof = 0.800996
A      = 5.04536 +/- 0.06028
lambda = 0.10405 +/- 0.00316
b      = 1.01925 +/- 0.03782
status = success

Os valores aproximados dos parâmetros são executados corretamente, e o valor do chi-quadrado indica um bom ajuste (o chi-quadrado por grau de liberdade é aproximadamente 1). Nesse caso os erros sobre os parâmetros podem ser estimados a partir das raízes quadradas dos elementos da diagonal da matriz de covariância.

Se o valor chi-quadrado mostra um ajuste pobre (i.e. chi^2/dof >> 1) então as estimativas de erro obtidas a partir da matriz de covariância irão ser muito pequenas. No programa exemplo as estimativas de erro são multiplicadas por \sqrt{\chi^2/dof} nesse caso, uma maneira comum de aumentar os erros para um ajuste pobre. Note que um ajuste pobre irá resultar do uso de um modelo inapropriado, e o erro proporcional estimado pode então sair fora do intervalo de validade para erros de Gauss.

38.12 Referências e Leituras Adicionais

O algoritmo MINPACK está descrito no seguinte artigo,

J.J. Moré, The Levenberg-Marquardt Algorithm: Implementation and Theory, Lecture Notes in Mathematics, v630 (1978), ed G. Watson.

O seguinte artigo é também relevante para os algoritmos descritos nessa seção,

J.J. Moré, B.S. Garbow, K.E. Hillstrom, “Testing Unconstrained Optimization Software”, ACM Transactions on Mathematical Software, Vol 7, No 1 (1981), p 17–41.

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.