37 Ajuste por Mínimos Quadrados

Esse capítulo descreve rotinas para executar ajustes por mínimos quadrados sobre dados experimentais usando combinações lineares de funções. Os dados podem ser ponderados ou não ponderados, i.e., com erros conhecidos ou desconhecidos. Para dados ponderados as funções calculam os melhores parâmetros de ajuste e sua matriz associada de covariância. Para dados não ponderados a matriz de covariância é estimada a partir da dispersão dos pontos, dando uma matriz de variância-covariância.

As funções são divididas em versões separadas para simples regressões de um ou dois parâmetros e ajustes de múltiplos parâmetros. As funções são declaradas no arquivo de cabeçalho ‘gsl_fit.h’.

37.1 Visão Geral

Ajustes de mínimos quadrados são encontrados minimizando \chi^2 (chi-quadrado), a soma ponderada dos resíduos quadrados sobre n pontos de dados experimentais (x_i, y_i) para o modelo Y(c,x),

As rotinas de ajuste retornam os parâmetros de melhor ajuste c e sua matriz de covariância p \times p. A matriz de covariância mede os erros estatísticos sobre os parâmetros de melhor ajuste contra os erros resultantes a partir dos erros sobre os dados, \sigma_i, e está definida como C_{ab} = <\delta c_a \delta c_b> onde < > denota uma média sobre as distribuições de erro de Gauss dos pontos de dados respectivos.

A matriz de covariância é calculada pela da propagação de erro a partir dos erros dos dados \sigma_i. A modificação em um parâmetro ajustado \delta c_a causada por uma pequena variação nos dados \delta y_i é dada por

O desvio padrão dos parâmetros de melhor ajuste são dados pela raíz quadrada dos correspondentes elementos da diagonal da matriz de covariância, \sigma_{c_a} = \sqrt{C_{aa}}. O coeficiente de correlação dos parâmetros de ajuste c_a e c_b é dado por \rho_{ab} = C_{ab} / \sqrt{C_{aa} C_{bb}}.

37.2 Regressão Linear

As funções descritas nessa seção podem ser usados para executar ajustes de mínimos quadrados para um modelo de linha reta, Y(c,x) = c_0 + c_1 x.

Function: int gsl_fit_linear (const double * x, const size_t xstride, const double * y, const size_t ystride, size_t n, double * c0, double * c1, double * cov00, double * cov01, double * cov11, double * sumsq)

Essa função calcula os coeficientes de regressão linear de melhor ajuste (c0,c1) do modelo Y = c_0 + c_1 X para o conjunto de dados (x, y), dois vetores de comprimento n com saltos xstride e ystride. Os erros sobre y são assumidos desconhecidos de forma que a matriz de variância-covariância para os parâmetros (c0, c1) é estimada a partir da dispersão dos pontos em torno da linha de melhor ajuste e retornado por meio de parâmetros (cov00, cov01, cov11). O somatório dos quadrados dos resíduos da linha de melhor ajuste é retornado em sumsq. Nota: o coeficiente de correlação dos dados pode ser calculado usando gsl_stats_correlation (veja seção Correlação), e não depende do ajuste.

Function: int gsl_fit_wlinear (const double * x, const size_t xstride, const double * w, const size_t wstride, const double * y, const size_t ystride, size_t n, double * c0, double * c1, double * cov00, double * cov01, double * cov11, double * chisq)

Essa função calcula os coeficientes de regressão linear do melhor ajuste (c0,c1) do modelo Y = c_0 + c_1 X para o conjunto de dados ponderados (x, y), dois vetores de comprimento n com saltos xstride e ystride. O vetor w, de comprimento n e salto wstride, especifica o peso da cada ponto de dados. O peso é o recíproco da variância para cada ponto de dados em y.

A matriz de covariância para os parâmetros (c0, c1) é calculada usando os pesos e retornada via parâmetros (cov00, cov01, cov11). A soma ponderada de quadrados dos resíduos da linha de melhor ajuste, \chi^2, é retornado em chisq.

Function: int gsl_fit_linear_est (double x, double c0, double c1, double cov00, double cov01, double cov11, double * y, double * y_err)

Essa função usa os coefcientes de regressão linear de melhor ajuste c0, c1 e suas covariância cov00, cov01, cov11 para calcular a função ajustada y e seu desvio padrão y_err para o modelo Y = c_0 + c_1 X no ponto x.

37.3 Ajuste linear sem um termo constante

As funções descritas nessa seção podem ser usadas para executar ajustes de mínimos quadrados para um modelo de linha reta sem um termo constante, Y = c_1 X.

Function: int gsl_fit_mul (const double * x, const size_t xstride, const double * y, const size_t ystride, size_t n, double * c1, double * cov11, double * sumsq)

Essa função calcula o coeficiente de regressão linear de melhor ajuste c1 do modelo Y = c_1 X para o conjunto de dados (x, y), dois vetores de comprimento n com saltos xstride e ystride. Os erros sobre y são assumidos desconhecidos de forma que a variância do parâmetro c1 é estimado a partir da dispersão dos pontos em torno da linha de melhor ajuste e retornado por meio do parâmetros cov11. A soma de quadrados dos resíduos da linha de melhor ajuste é retornado em sumsq.

Function: int gsl_fit_wmul (const double * x, const size_t xstride, const double * w, const size_t wstride, const double * y, const size_t ystride, size_t n, double * c1, double * cov11, double * sumsq)

Essa função calcula o coeficiente de regressão linear de melhor ajuste c1 do modelo Y = c_1 X para o conjunto de dados ponderados (x, y), dois vetores de comprimento n com saltos xstride e ystride. O vetor w, de comprimento n e salto wstride, especifica o peso de cada ponto de dados. O peso é o recíproco da variância para cada ponto de dado em y.

A variância do parâmetro c1 é calculada usando os pesos e retornado via parâmetro cov11. A soma ponderada de quadrados dos resíduos da linha de melhor ajuste, \chi^2, é retornado em chisq.

Function: int gsl_fit_mul_est (double x, double c1, double cov11, double * y, double * y_err)

Essa função usa o coeficiente de regressão linear de melhor ajuste c1 e sua covariância cov11 para calcular a função ajustada y e seu desvio padrão y_err para o modelo Y = c_1 X no ponto x.

37.4 Ajuste de Parâmetros Multidimensionais

As funções descritas nessas seções executam ajustes de mínimos quadrados para um modelo linear geral, y = X c onde y é um vetor de n observações, X é uma matriz de n por p de variáveis do previsor, e os elementos do vetor c são os p parâmetros desconhecidos de melhor ajuste que são para serem estimados. O valor do chi-quadrado é dado por \chi^2 = \sum_i w_i (y_i - \sum_j X_{ij} c_j)^2.

Essa formulação pode ser usada para ajustes em qualquer número de funções e/ou variáveis preparando a matriz X de ordem n-por-p apropriadamente. Por exemplo, para ajustar um polinômio de p-ésima ordem em x, use a seguinte matriz,

Para ajustar um conjutno de p funções sinusoidais com frequências fixadas \omega_1, \omega_2, …, \omega_p, use,

As funções descritas nessa seção são declaradas no arquivo de cabeçalho ‘gsl_multifit.h’.

A solução do sistema de mínimos quadrados linear geral requer um espaço de trabalho adicional para resultados intermediários, tal como a decomposição de valor singular da matriz X.

Function: gsl_multifit_linear_workspace * gsl_multifit_linear_alloc (size_t n, size_t p)

Essa função aloca um espaço de trabalho para ajustar um modelo para n observações usando p parâmetros.

Function: void gsl_multifit_linear_free (gsl_multifit_linear_workspace * work)

Essa função libera a memória associada ao espaço de trabalho w.

Function: int gsl_multifit_linear (const gsl_matrix * X, const gsl_vector * y, gsl_vector * c, gsl_matrix * cov, double * chisq, gsl_multifit_linear_workspace * work)

Essa função calcula os parâmetros de melhor ajuste c do modelo y = X c para as observações y e a matriz das variáveis do previsor X, usando o espaço de trabalho pré-alocado fornecido em work. A matriz de variância-covariância de ordem p-por-p dos parâmetros do modelo cov é akiustado para \sigma^2 (X^T X)^{-1}, onde \sigma é o desvio padrão dos ajustes residuais. A soma de quadrados dos residuias a partir do melhor ajuste, \chi^2, é retornado em chisq. Se o coeficiente de determinação é desejado, pode ser calculado a partir da expressão R^2 = 1 - \chi^2 / TSS, onde o somatório total dos quadrados (TSS) das observações y pode ser calculado a partir de gsl_stats_tss.

O melhor ajuste é encontrado por uma decomposição de valor singular da matriz X usando o algoritmo SVD de Golub-Reinsch odificado, com ajuste proporcioanl de coluna para melhorar a precisão dos valores singulares. Quaisquer componentes que possuem valor singular zero (para precisão de máquina) são descartados a partir do ajuste.

Function: int gsl_multifit_wlinear (const gsl_matrix * X, const gsl_vector * w, const gsl_vector * y, gsl_vector * c, gsl_matrix * cov, double * chisq, gsl_multifit_linear_workspace * work)

Essa função calcula os parâmetros de melhor ajuste c do modelo ponderado y = X c para as observações y com pesos w e a matriz de variáveis do previsor X, usando o espaço de trabalho pré-alocado fornecido em work. A matriz p-por-p de covariância dos parâmetros do modelo cov é calculada como (X^T W X)^{-1}. A soma ponderada de quadrados dos resíduos do melhor ajuste, \chi^2, é retornado em chisq. Se o coeficiente de determinação for desejado, pode ser calculado a partir da expressão R^2 = 1 - \chi^2 / WTSS, onde a soma total de quadrados ponderados (WTSS) das observações y podem ser calculadas a partir de gsl_stats_wtss.

Function: int gsl_multifit_linear_svd (const gsl_matrix * X, const gsl_vector * y, double tol, size_t * rank, gsl_vector * c, gsl_matrix * cov, double * chisq, gsl_multifit_linear_workspace * work)

Function: int gsl_multifit_wlinear_svd (const gsl_matrix * X, const gsl_vector * w, const gsl_vector * y, double tol, size_t * rank, gsl_vector * c, gsl_matrix * cov, double * chisq, gsl_multifit_linear_workspace * work)

Nesses componentes de função do ajuste são descartados se a razão de valores singulares s_i/s_0 cai abaixo da tolerância especificada pelo usuário tol, e o posto efetivo é retornado em rank.

Function: int gsl_multifit_linear_usvd (const gsl_matrix * X, const gsl_vector * y, double tol, size_t * rank, gsl_vector * c, gsl_matrix * cov, double * chisq, gsl_multifit_linear_workspace * work)

Function: int gsl_multifit_wlinear_usvd (const gsl_matrix * X, const gsl_vector * w, const gsl_vector * y, double tol, size_t * rank, gsl_vector * c, gsl_matrix * cov, double * chisq, gsl_multifit_linear_workspace * work)

Essas funções calculam o ajuste usando SVD (74)sem escalonamento de colunas.

Function: int gsl_multifit_linear_est (const gsl_vector * x, const gsl_vector * c, const gsl_matrix * cov, double * y, double * y_err)

Essa função usa os coeficientes de regressão multilinear de melhor ajuste c e sua matriz de covariância cov para calcular o valor da função ajustada y e seu desvio padrão y_err para o modelo y = x.c no ponto x.

Function: int gsl_multifit_linear_residuals (const gsl_matrix * X, const gsl_vector * y, const gsl_vector * c, gsl_vector * r)

Essa função calcula o vetor de resíduos r = y - X c para as observações y, coeficientes c e matriz de variáveis do previsor X.

37.5 Regressão linear robusta

Modelos de mínimos quadrados comuns (OLS) são muitas vezes grandemente influenciados pela presença de outliers. Outliers são pontos de dados que não seguem a tendência geral de outras observações, embora não exista definição precisa de um outlier. Regressão linear robusta refere-se a algorítimos de regressão que são resistentes a outliers. O tipo mais comum de regressão robusta é a estimação-M. O M-estimador geral minimiza a função objetivo onde e_i = y_i - Y(c, x_i) é o resíduo do i-ésimo ponto de dados, e \rho(e_i) é uma função que deve ter as seguintes propriedades:

• \rho(e) \ge 0
• \rho(0) = 0
• \rho(-e) = \rho(e)
• \rho(e_1) > \rho(e_2) for |e_1| > |e_2|

O caso especial de mínimos quadrados comuns é dado por \rho(e_i) = e_i^2. Façamos \psi = \rho' ser a derivada de \rho, diferenciando a função objetivo em relação aos coeficientes c e ajustando as derivadas parciais para zero produzimos o sistema de equações onde X_i é um vetor contendo i linhas da matriz de design X. Adiante, definimos uma função peso w(e) = \psi(e)/e, e tomemos w_i = w(e_i): O sistema de equações é equivalenete a resolver um problema de mínimos quadrados comuns ponderado, minimizando \chi^2 = \sum_i w_i e_i^2. Os pesos todavia, dependem dos resíduos e_i, os quais dependem dos coeficientes c, que por sua vez dependem dos pesos. Portanto, uma solução iterativa é usada, chamada Mínimos Quadrados Iterativamente Reponderados (Iteratively Reweighted Least Squares - IRLS).

1. Calcula estimativas iniciais dos coeficientes c^{(0)} usando mínimos quadrados comuns
2. Para a iteração k, forma-se os resíduos e_i^{(k)} = (y_i - X_i c^{(k-1)})/(t \sigma^{(k)} \sqrt{1 - h_i}), onde t é uma constante de ajuste dependente da escolha de \psi, e h_i são os maximizadores estatísticos (elementos da diagonal da matriz X (X^T X)^{-1} X^T). Incluindo t e h_i no cálculo do residual melhora a convergência do método. O desvio padrão do resíduo é é aproximado como \sigma^{(k)} = MAD / 0.6745, onde MAD é o desvio médio absoludo (Median-Absolute-Deviation) dos n-p maiores resíduos a partir da iteração anterior.
3. Calcula novos pesos w_i^{(k)} = \psi(e_i^{(k)})/e_i^{(k)}.
4. Calcula novos coeficientes c^{(k)} resolvendo o problema de mínimos quadrados ponderados com pesos w_i^{(k)}.
5. Passos 2 a 4 são iterados até que os coeficientes sejam convergentes para algum limite máximo de iteração alcançado. Coeficientes são testados para convergência usando o critério: para todo 0 \le i < p onde \epsilon é um pequeno fator de tolerância.

A chave para esse método encontra-se na seleção da função \psi(e_i) para atribuir pequenos pesos a grandes resíduos, e grandes pesos a pequenos resíduos. Com a continuidade da iteração, outliers recebem pesos cada vez menores, eventualmente tendo muito pequeno ou nenhum efeito no modelo ajustado.

Function: gsl_multifit_robust_workspace * gsl_multifit_robust_alloc (const gsl_multifit_robust_type * T, const size_t n, const size_t p)

Essa função aloca um espaço de trabalho para o ajuste de um modelo para n observaçõe usando p parâmetros. O tipo T especifica a função \psi e pode ser selecionado a partir das seguintes escolhas.

Robust type: gsl_multifit_robust_default

Especifica o tipo gsl_multifit_robust_bisquare (veja abaixo) e é uma boa escolha de propósito geral para regressão robusta.

Robust type: gsl_multifit_robust_bisquare

Essa é a função duplo-peso de Tukey (biquadrada) e é uma boa escolha de propósito geral para regressão robusta. A função peso é dada por e a constante de ajuste padrão é t = 4.685.

Robust type: gsl_multifit_robust_cauchy

É a função de Cauchy, também conhecida como a função Lorentziana. Essa função não garate uma solução única, significando que diferentes escolhas do vetor c dos coeficientes podem vir a minimizar a função objetivo. Portanto essa opção deve ser usada com cuidado. A fução peso é dada por e a constante de ajuste padrão é t = 2.385.

Robust type: gsl_multifit_robust_fair

É a função \rho adequada, que garante uma solução única e tem derivadas contínuas para três ordens. A função peso é dada por e a constane de ajsute padrão é t = 1.400.

Robust type: gsl_multifit_robust_huber

Especifica a função \rho de Huber, que é uma parábola próxima do zero e cresce linearmente para um dado limiar |e| > t. Essa função é também considerada um excelente estimador de propósito geral para a regressão linear robusta, todavia, dificuldades ocasionais podem ser encontradas devido a descontinuidades na primeira derivada da função \psi. A função peso é dada por e a constante de ajuste padrão é t = 1.345.

Robust type: gsl_multifit_robust_ols

Especifica a solução por mínimos quadrados comum, que pode ser útil para rapidamente verificar a diferença entre as soluções pelo método robusto e pelo método por mínimos quadrados (OLS). A função peso é dada por e a constante de ajuste padrão é t = 1.

Robust type: gsl_multifit_robust_welsch

Especifica a função de Welsch que pode executar bem nos casos onde os resíduos possuem uma distribuição exponencial. A função peso é dada por e a constante de ajuste padrão é t = 2.985.

Function: void gsl_multifit_robust_free (gsl_multifit_robust_workspace * w)

Essa função libera e memória associada ao espaço de trabalho w.

Function: const char * gsl_multifit_robust_name (const gsl_multifit_robust_workspace * w)

Essa função retorna o nome do tipo robusto T especificado para gsl_multifit_robust_alloc.

Function: int gsl_multifit_robust_tune (const double tune, gsl_multifit_robust_workspace * w)

Essa função ajusta a constante de ajuste t usada para ajustar o resíduo a cada iteração para tune. Decrescendo a constante de ajuste aumenta-se o peso baixo atribuído a grandes resíduos, enquanto aumentando a constante de ajuste diminui-se o baixo peso atribuído a grandes resíduos.

Function: int gsl_multifit_robust (const gsl_matrix * X, const gsl_vector * y, gsl_vector * c, gsl_matrix * cov, gsl_multifit_robust_workspace * w)

Essa função calcula os parametros de melhor ajuste c do modelo y = X c para as observações y e a matriz das variáveis do preditor X, tentando reduir a influência dos outliers usando o algorítmo outlinado acima. A matriz de variância-covariância de ordem p-por-p dos parâmetros do modelo cov é estimada como \sigma^2 (X^T X)^{-1}, onde \sigma é uma aproximação do desvio padrão do resíduo usando a teoria da regressão robusta. Cuidado especial deve ser tomado ao se estimar \sigma e outras estatísticas tais como R^2, e então \sigma e essas outras estatísticas são calculados internamente e estão dispoíveis chamando a função gsl_multifit_robust_statistics.

Function: int gsl_multifit_robust_est (const gsl_vector * x, const gsl_vector * c, const gsl_matrix * cov, double * y, double * y_err)

Essa função utiliza os coeficientes de melhor ajuste da regressão robusta c e sua matriz de covariância cov para calcular o valor de função ajustado y e seu desvio padrão y_err para o modelo y = x.c no ponto x.

Function: gsl_multifit_robust_stats gsl_multifit_robust_statistics (const gsl_multifit_robust_workspace * w)

Esssa função retorna uma estrutura contendo estatísticas relevantes a partir de uma regressão robusta. A função gsl_multifit_robust deve ser chamada primeiramente para executar a regressão e calcular essas estatísticas. A estrutura retornada gsl_multifit_robust_stats contém os seguintes campos.

• double sigma_ols Contém o desvio padrão dos resíduos como calculado a partir do mínimos quadrados comuns (OLS).
• double sigma_mad Contém uma estimativa do desvio padrão dos resíduos finais usando a estatística do Desvio Absoluto Mediano.
• double sigma_rob Contém uma estimativa do desvio padrão dos resíduos finais a partir da teoria da regressão robustan (veja Street et al, 1988).
• double sigma Contém uma estimativa do desvio padrão dos resíduos finais por tentativa de reconciliação entre sigma_rob e sigma_ols de uma forma razoável.
• double Rsq Contém o coeficiente R^2 de estatística de determinação usando a estimativa sigma.
• double adj_Rsq Contém o coeficiente R^2 ajustado de estatística de determinação usando o sigma estimado.
• double rmse Contém o erro quadrático médio dos resíduos finais.
• double sse Contém a soma de quadrados residual feita a partir da matrix de covariancia robusta.
• size_t dof Contém o número de graus de liberdade n - p.
• size_t numit Objetivando uma convergência eficiente, contém o número de iterações executado.
• gsl_vector * weights Contém o vetor de peso final de comprimento n
• gsl_vector * r Contém o vetor de resíduo final de comprimento n, r = y - X c

37.6 Evitando de problemas

Durante o uso de modelos baseados em polinômios, cuidado deve ser tomado ao se construir a matriz design X. Se os valores x forem grandes, então a matriz X pode ser ill-condicionada uma vez que suas colunas são potências de x, conduzindo a soluções por mínimos quadrados instáveis. Nesse caso pode muitas vezes ajudar a centralizar e ajustar proporcionalmente os valores de x usando a média e o desvio padrão: e então construir a matriz X usando os valores transformados x'.

37.7 Exemplos

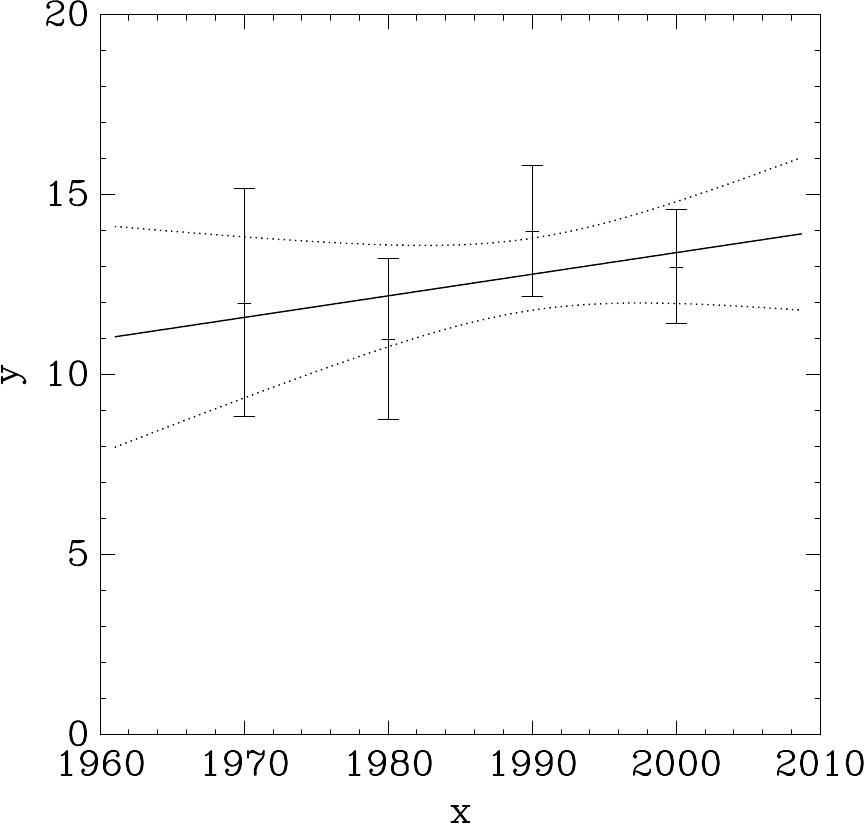
O seguinte programa calcula um ajuste de linha reta de mínimos quadrados para um conjunto de dados simples, e saídas a linha de melhor ajuste e sua barras de erro de desvio padrão associadas.

#include <stdio.h>
#include <gsl/gsl_fit.h>

int
main (void)
{
  int i, n = 4;
  double x[4] = { 1970, 1980, 1990, 2000 };
  double y[4] = {   12,   11,   14,   13 };
  double w[4] = {  0.1,  0.2,  0.3,  0.4 };

  double c0, c1, cov00, cov01, cov11, chisq;

  gsl_fit_wlinear (x, 1, w, 1, y, 1, n, 
                   &c0, &c1, &cov00, &cov01, &cov11, 
                   &chisq);

  printf ("# best fit: Y = %g + %g X\n", c0, c1);
  printf ("# covariance matrix:\n");
  printf ("# [ %g, %g\n#   %g, %g]\n", 
          cov00, cov01, cov01, cov11);
  printf ("# chisq = %g\n", chisq);

  for (i = 0; i < n; i++)
    printf ("data: %g %g %g\n", 
                   x[i], y[i], 1/sqrt(w[i]));

  printf ("\n");

  for (i = -30; i < 130; i++)
    {
      double xf = x[0] + (i/100.0) * (x[n-1] - x[0]);
      double yf, yf_err;

      gsl_fit_linear_est (xf, 
                          c0, c1, 
                          cov00, cov01, cov11, 
                          &yf, &yf_err);

      printf ("fit: %g %g\n", xf, yf);
      printf ("hi : %g %g\n", xf, yf + yf_err);
      printf ("lo : %g %g\n", xf, yf - yf_err);
    }
  return 0;
}

Os seguintes comandos extraem os dados a partir de uma saída do programa e mostra isso usando o utilitário graph do pacote GNU plotutils,

$ ./demo > tmp
$ more tmp
# best fit: Y = -106.6 + 0.06 X
# covariance matrix:
# [ 39602, -19.9
#   -19.9, 0.01]
# chisq = 0.8

$ for n in data fit hi lo ; 
   do 
     grep "^$n" tmp | cut -d: -f2 > $n ; 
   done
$ graph -T X -X x -Y y -y 0 20 -m 0 -S 2 -Ie data 
     -S 0 -I a -m 1 fit -m 2 hi -m 2 lo

O seguinte programa executa um ajuste quadrático y = c_0 + c_1 x + c_2 x^2 para um conjunto de dados ponderados usando a função de ajuste linear ponderado generalizado gsl_multifit_wlinear. A matriz modelo X para um ajuste quadrático é dado por,

O programa lê n linhas de dados no formato (x, y, err) onde err é o erro (desvio padrão) no valor y.

#include <stdio.h>
#include <gsl/gsl_multifit.h>

int
main (int argc, char **argv)
{
  int i, n;
  double xi, yi, ei, chisq;
  gsl_matrix *X, *cov;
  gsl_vector *y, *w, *c;

  if (argc != 2)
    {
      fprintf (stderr,"usage: fit n < data\n");
      exit (-1);
    }

  n = atoi (argv[1]);

  X = gsl_matrix_alloc (n, 3);
  y = gsl_vector_alloc (n);
  w = gsl_vector_alloc (n);

  c = gsl_vector_alloc (3);
  cov = gsl_matrix_alloc (3, 3);

  for (i = 0; i < n; i++)
    {
      int count = fscanf (stdin, "%lg %lg %lg",
                          &xi, &yi, &ei);

      if (count != 3)
        {
          fprintf (stderr, "error reading file\n");
          exit (-1);
        }

      printf ("%g %g +/- %g\n", xi, yi, ei);
      
      gsl_matrix_set (X, i, 0, 1.0);
      gsl_matrix_set (X, i, 1, xi);
      gsl_matrix_set (X, i, 2, xi*xi);
      
      gsl_vector_set (y, i, yi);
      gsl_vector_set (w, i, 1.0/(ei*ei));
    }

  {
    gsl_multifit_linear_workspace * work 
      = gsl_multifit_linear_alloc (n, 3);
    gsl_multifit_wlinear (X, w, y, c, cov,
                          &chisq, work);
    gsl_multifit_linear_free (work);
  }

#define C(i) (gsl_vector_get(c,(i)))
#define COV(i,j) (gsl_matrix_get(cov,(i),(j)))

  {
    printf ("# best fit: Y = %g + %g X + %g X^2\n", 
            C(0), C(1), C(2));

    printf ("# covariance matrix:\n");
    printf ("[ %+.5e, %+.5e, %+.5e  \n",
               COV(0,0), COV(0,1), COV(0,2));
    printf ("  %+.5e, %+.5e, %+.5e  \n", 
               COV(1,0), COV(1,1), COV(1,2));
    printf ("  %+.5e, %+.5e, %+.5e ]\n", 
               COV(2,0), COV(2,1), COV(2,2));
    printf ("# chisq = %g\n", chisq);
  }

  gsl_matrix_free (X);
  gsl_vector_free (y);
  gsl_vector_free (w);
  gsl_vector_free (c);
  gsl_matrix_free (cov);

  return 0;
}

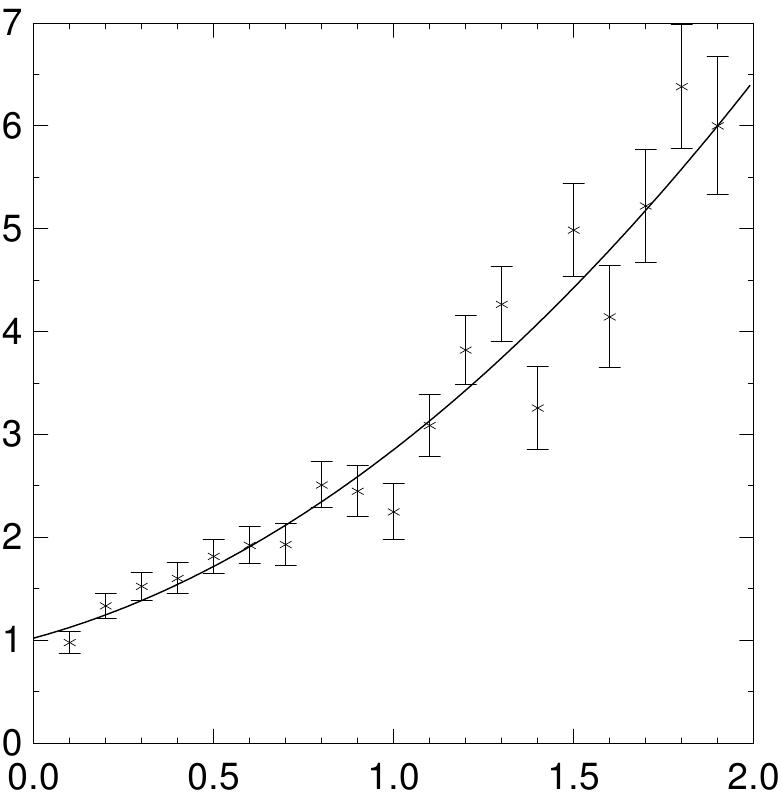
Um adequado conjunto de dados para ajustes pode ser gerado usando o seguinte programa. A saída é um conjunto de pontos com erros de Gauss da curva y = e^x na região 0 < x < 2.

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_randist.h>

int
main (void)
{
  double x;
  const gsl_rng_type * T;
  gsl_rng * r;
  
  gsl_rng_env_setup ();
  
  T = gsl_rng_default;
  r = gsl_rng_alloc (T);

  for (x = 0.1; x < 2; x+= 0.1)
    {
      double y0 = exp (x);
      double sigma = 0.1 * y0;
      double dy = gsl_ran_gaussian (r, sigma);

      printf ("%g %g %g\n", x, y0 + dy, sigma);
    }

  gsl_rng_free(r);

  return 0;
}

Os dados podem ser preparados rodando o programa executável,

$ GSL_RNG_TYPE=mt19937_1999 ./generate > exp.dat
$ more exp.dat
0.1 0.97935 0.110517
0.2 1.3359 0.12214
0.3 1.52573 0.134986
0.4 1.60318 0.149182
0.5 1.81731 0.164872
0.6 1.92475 0.182212
....

Para ajustar os dados use o programa anterior, como número de pontos de dados fornecido como o primeiro argumento. Nesse caso existem 19 pontos de dados.

$ ./fit 19 < exp.dat
0.1 0.97935 +/- 0.110517
0.2 1.3359 +/- 0.12214
...
# best fit: Y = 1.02318 + 0.956201 X + 0.876796 X^2
# covariance matrix:
[ +1.25612e-02, -3.64387e-02, +1.94389e-02  
  -3.64387e-02, +1.42339e-01, -8.48761e-02  
  +1.94389e-02, -8.48761e-02, +5.60243e-02 ]
# chisq = 23.0987

Os parâmetros do ajuste quadrático coincidem com os coeficientes da expansão de e^x, tomados na contabilidade dos erros sobre os parâmetros e a diferença O(x^3) entre as funções exponencial e quadráticas para o maior valor de x. O erros sobre os parâmetros são dados pela raíz quadrada dos correspondentes elementos da diagonal da matriz de covariância. O chi-quadrado por grau de liberdade é 1.4, indicando um ajuste razoável para os dados.

37.8 Referências e Leituras Adicionais

Um sumário de fórmulas e técnicas para ajuste por mínimos quadrados pode ser encontrado no capítulo “Statisticals” do “Annual Review of Particle Physics” preparado pelo “Particle Data Group”,

• Review of Particle Properties, R.M. Barnett et al., Physical Review D54, 1 (1996) http://pdg.lbl.gov/

O “Review of Particle Physics” está disponível online no sítio dado abaixo.

Os testes usados para preparar essas rotinas são baseados no NIST Statistical Reference Datasets. Os conjuntos de dados e sua documentação estão disponíveis no NIST no seguinte sítio,

http://www.nist.gov/itl/div898/strd/index.html.

A implementação da GSL da regressão linear robusta segue de perto as publicações

• DuMouchel, W. and F. O’Brien (1989), "Integrating a robust option into a multiple regression computing environment," Computer Science and Statistics: Proceedings of the 21st Symposium on the Interface, American Statistical Association
• Street, J.O., R.J. Carroll, and D. Ruppert (1988), "A note on computing robust regression estimates via iteratively reweighted least squares," The American Statistician, v. 42, pp. 152-154.

Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.