| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse capítulo descreve rotinas para procurar mínimos locais de funções multidimensionais arbitrárias. A biblioteca fornece componentes de baixo nível para uma variedade de minimizadores iterativos e testes de convergência. Esses minimizadores e testes podem ser combinados pelo usuário para encontrar a solução desejada, enquanto fornece acessos total aos passos intermediários dos algoritmos. Cada classe de métodos usa a mesma estrutura, de forma que você pod alternar entre os minimizadores nanhora da execução sem ter que recompilar seu programa. Cada instância de um minimizador mantém registros de seu próprio estado, permitindo que os minimizadores sejam usados em programas com suporte a múltiplas linhas de execução. Os algoritmos de minimização possam ser usados para maximizar uma função invertendo seu signal.
O arquivo de cabeçalho ‘gsl_multimin.h’ contém protótipos para funções de minimização e delarações relacionadas.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
O problema de minimização multidimensional requer encontrar um ponto
x tal que a função escalar,
|
Algoritmos fazendo uso do coeficiente angular da função executam uma redução ao mínimo unidimensional sobre a linha da função ao longo da direção do coeficiente angular até que o menor ponto seja encontrado para uma adequada tolerância. A direção de busca é então atualizada com informação local a partir da função e suas derivadas, e o processo todo é repetido até que o verdadeiro mínimo local n-dimensional seja encontrado.
Algoritmos que não requerem o coeficiente angular da função usam diferentes estratégias. Por exemplo, o algoritmos Simples de Nelder-Mead mantém n+1 vetores de parâmetros de teste como os vértices de um simplex (71)n-dimensional. A cada iteração os algoritmo tenta melhorar o pior vértice do simplex por transformações geométricas. As iterações são continuadas até que o tamanho geral do simplex tenha descrescendo suficientemente.
Ambos os tipos de algoritmos usam uma estrutura padronizada. O usuário fornece um norteador de alto nível para os algoritmos, e a biblioteca fornece as funções individuais necessárias a cada um dos passos. Existem três principais fases da iteração. Os passos são,
Cada passo de iteração consiste ou de uma melhora na
redução ao mínimo na linha da função na direção atual ou uma atualização na direção de
busca propriamente dita. O estado dos minimizadores é mantido em uma
estrutura gsl_multimin_fdfminimizer ou em uma
estrutura gsl_multimin_fminimizer.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Note que os algoritmos de minimização podem somente buscar um mínimo local a cada vez. Quando houverem muitos mínimos locais na área de busca, o primeiro mínimo a ser encontrado ierá ser retornado; todavia é difícil predizer qual dos mínimos ele irá ser. Na maioria dos casos, nenhum erro irá ser informado se você tentar encontrar um mínimo local em uma área onde existe mais de um.
É também importante notar que o algoritmo de minimização encontra mínimos locais; não existe caminho para determinar se um mínimo é um mínimo global da função em questão.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
A seguinte função inicializa um minimizador multidimensional. O minimizador propriamente dito depende somente da dimensão do problema e do algoritmo e pode ser reaproveitado por diferentes problemas.
Essa função rtorna um apontador para uma recentemente alocada intância de uma
minimizador do tipo T para uma função n-dimensional. Se não houver
memória suficiente para criar o minimizador então a função retorna
um apontador nulo e o manipulador de erro é chamado com um código de erro de
GSL_ENOMEM.
A função gsl_multimin_fdfminimizer_set inicializa o minimizador s para minimizar a função
fdf iniciando a partir do ponto inicial x. O tamanho do
primeiro passo de teste é fornecido por step_size. A precisão da minimização
sobre a linha da função é especificada por tol. O significado preciso desse
parâmetro depende do método usado. Tipicamente a minimização de linha
é considerada com sucesso se o coeficiente angular da função g é
ortogonal à atual direção de busca p para uma precisão
relativa de tol, onde dot(p,g) < tol |p| |g|. Um valor tol de 0.1 é
adequado para a maioria dos propósitos, uma vez que minimização de linha somente precisa de
ser realizada de forma aproximada. Note que ajustando tol para zero irá
forçar o uso de buscas de linha “exatas”, que são extremamente dispendiosas.
A função gsl_multimin_fminimizer_set inicializa o minimizador s para minimizar a função
f, iniciando a partir do ponto inicial
x. O tamanho dos passos de teste iniciais é fornecido em um vetor
step_size. O preciso significado desse parâmetro depende do
método usado.
Essa função libera toda a memória associada ao minimizador s.
Essa função retorna um apntador para o nome do minimizador. Por exemplo,
printf ("s é um minimizador '%s'\n",
gsl_multimin_fdfminimizer_name (s));
pode imprimir alguma coisa como s é um minimizador 'conjugate_pr'.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Você deve fornecer uma função paramétrica de n variáveis para o minimizador trabalhar sobre ela. Você pode tambémprecisar fornecer uma rotina que calcula o da função e uma terceira rotina que calcula ambos o valor de função e o coeficiente angular juntos. Com o objetivo de permitir parâmetros gerais as funções são definidas pelos seguintes tipos de dado:
Esses tipos de dados definem uma função geral de n variáveis com parâmetros e o correspondente vetor de coeficientes angulare de derivadas,
double (* f) (const gsl_vector * x, void * params)essa função deve retornar o resultado
f(x,params) para o argumento x e parâmetros params.
Se a função não puder ser calculada, um valor de erro de GSL_NAN
deve ser retornado.
void (* df) (const gsl_vector * x, void * params, gsl_vector * g)essa função deve armazenar o coeficiente angular n-dimensional g_i = d f(x,params) / d x_i in the vector g for argument x e parâmetros params, retornando um código de erro apropriando se a função não puder ser calculado.
void (* fdf) (const gsl_vector * x, void * params, double * f, gsl_vector * g)Essa função de ajustar os valores de f e g como mostrado acima, para arugmentos x e parâmetros params. Essa função fornece uma otimização de funções separadas para f(x) e g(x)—é sempre mais rápido calcular a função e sua derivada ao mesmo tempo.
size_t na dimensão do sistema, i.e. o número de componentes dos vetores x.
void * paramsum apontador para os parâmetros da função.
Esses tipos de dados definem uma função geral de n variáveis com parâmetros,
double (* f) (const gsl_vector * x, void * params)essa função deve retornar o resultado
f(x,params) para argumento x e parâmetros params.
Se a função não puder ser calculada, um valor de erro de GSL_NAN
deve ser retornado.
size_t na dimensão do sistema, i.e. o número de componentes dos vetores x.
void * paramsum apontador para os parâmetros da função.
A seguinte função exemplo define um parabolóide simples bidimensional com cinco parâmetros,
/* Paraboloid centered on (p[0],p[1]), with
scale factors (p[2],p[3]) and minimum p[4] */
double
my_f (const gsl_vector *v, void *params)
{
double x, y;
double *p = (double *)params;
x = gsl_vector_get(v, 0);
y = gsl_vector_get(v, 1);
return p[2] * (x - p[0]) * (x - p[0]) +
p[3] * (y - p[1]) * (y - p[1]) + p[4];
}
/* The gradient of f, df = (df/dx, df/dy). */
void
my_df (const gsl_vector *v, void *params,
gsl_vector *df)
{
double x, y;
double *p = (double *)params;
x = gsl_vector_get(v, 0);
y = gsl_vector_get(v, 1);
gsl_vector_set(df, 0, 2.0 * p[2] * (x - p[0]));
gsl_vector_set(df, 1, 2.0 * p[3] * (y - p[1]));
}
/* Compute both f and df together. */
void
my_fdf (const gsl_vector *x, void *params,
double *f, gsl_vector *df)
{
*f = my_f(x, params);
my_df(x, params, df);
}
A função pode ser inicializadqa usando o seguinte código,
gsl_multimin_function_fdf my_func;
/* Paraboloid center at (1,2), scale factors (10, 20),
minimum value 30 */
double p[5] = { 1.0, 2.0, 10.0, 20.0, 30.0 };
my_func.n = 2; /* number of function components */
my_func.f = &my_f;
my_func.df = &my_df;
my_func.fdf = &my_fdf;
my_func.params = (void *)p;
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
A seguinte função norteia a iteração de cada algoritmo. A função executa uma iteração para atualizar o estado do minimizador. A mesma função trabalha para todos os minimizadores de forma que diferentes métodos podem ser substituídos durante a execução sem modificações no código.
Essas funções executam uma iteração simples do minimizador s.
Se a iteração encontrar um problema inesperado então um código de erro
irá ser retornado. O código de erro GSL_ENOPROG significa que
o minimzador é incapaz de melhorar usando a estimativa atual, ou devido a
dificuldades numéricas ou pelo fato de que um mínimo local genuído tenha sido
alcançado.
O minimizador amnté uma atual melhor estimativa do mínimo em todas as vezes. essa informação pode ser acessada com as seguintes funções auxiliares,
Essas funções retornam a atual melhor estimativa de localização do mínimo, o valor da função naquele ponto, seu coeficiente angular, e tamanho característico específico do minimizador para o minimizador s.
Essa função zera o minimizador s para usar o ponto atual como um novo ponto inicial.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Um procedimento de minimização deve parar quando uma das seguintes condições for verdadeira:
A manipulação dessas condições está sob controle do usuário. As funções abaixo permitem ao usuário testar a precisão do resultado atual.
Essa função testa o módulo do coeficiente angular g contra a
tolerância absoluta epsabs. O coeficiente angular de uma função
função multidimensional vai para zero em ummínimo. O teste retorna GSL_SUCCESS
se a seguinte condição for encontrada,
|
GSL_CONTINUE de outra forma. Uma escolha adequada de
epsabs pode ser feita a partir da precisão desejada na função para
pequenas variações em x. O relacionamento entre essas quantidades
é dado por \delta f = g \delta x.
Essa função testa o tamanho característico específico do minimizador
(se aplicável ao minimizador em uso) contra a tolerância absoluta epsabs.
O teste retorna GSL_SUCCESS se o tamanho for menor que a tolerância,
de foutra forma GSL_CONTINUE é retornado.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Existem muitos métodos de minimização disponíveis. A melhor escolha do algoritmo depende do problema. Os algoritmos descritos nessa seção usam o valor da função e seu coeficiente angular em cada ponto de avaliação.
Esse é o algoritmo de coeficienete angular conjugado de Fletcher-Reeveste. O algoritmo de coeficiene angular conjugado trabalha como uma sucessão de minimizações de linha. A sequência de direções de busca é usada para construir uma aproximação para a curvatura da função nas vizinhanças do mínimo local.
Uma direção de busca inicial p é modificada usando o coeficiente angular, e uma minimização de linha é realizada naquela direção. A precisão da minimização de linha é especificada pelo parâmetro tol. O mínimo ao longo dessa linha ocorre quando o coeficiente angular da função g e a busca de direção p forem ortogonais. A minimização de linha termina quando dot(p,g) < tol |p| |g|. A direção de busca é atualizada usando a fórmula de Fletcher-Reeves p' = g' - \beta g onde \beta=-|g'|^2/|g|^2, e a minimização de linha é então repetida para a nova direção de busca.
Esse é o algoritmo de coeficiente angular conjugado de Polak-Ribiere. É similar ao método de Fletcher-Reeves, diferindo somente na escolha do coeficiente \beta. Ambos os métodos trabalham bem quando o ponto de avaliação é próximo o suficiente do mínimo da função objetiva que é bem aproximada por uma hipersuperfície quadrática.
Esses métodos usam o algoritmo Broyden-Fletcher-Goldfarb-Shanno (BFGS) de vetor. Esse é um método quasi-Newton que constrói uma aproximação para a seguunda derivada da função f usando a diferença entre sucessivos vetores de coeficiente angular. Pela combinação da primeira e da segunda derivadas o algoritmo está apto a tomar passos do tipo usado no método de Newton na direção do mínimo da função, assumindo comportamento quadrático naquela região.
A versão bfgs2 desse minimizador é mais eficiente
versão disponível, e é uma implentação fiel do esquema de
minimização de linha descrito no artigo de Fletcher Practical Methods of
Optimization, Algoritmos 2.6.2 e 2.6.4. Supera a rotina
bfgs original e requer substancialmente poucas avaliações de
função e coeficiente angular. A tolerância fornecida pelo usuário tol
corresponde ao parâmetro \sigma usado por Fletcher. Um valor
de 0.1 é recomendado para uso comum (maiores valores correspondem a
buscas de linha menos precisas).
O algoritmo extremamente íngreme e descendente segue o coeficiente angular morro abaixo da função a cada passo. Quando um passo morro abaixo é dado com sucesso o tamanho de passo é aumentado por um fator de dois. Se o passo morro abaixo conduzir a um muito maior valor de função então o algoritmo volta usando os reistros mantidos internamente e o tamanho de passo é diminuído usando o parâmetro tol. Um valor adequado de tol para a maioria das aplicações é 0.1. O método exageradamente íngreme e descendente é ineficiente e está incluído somente para propósitos de demonstração.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Os algoritmos descritos nessa seção usam somente o valor da função a cada ponto de avaliação.
Esses métodos usam o algoritmo Simplex de Nelder e Mead.
Iniciando a partir do vetor inicial x = p_0, o algoritmo
constrói adicionais n vectores do tipo p_i
usando o vetor de tamanho de passo s = step_size como segue:
|
Após cada iteração, o melhor vértice é retornado. Note, que devido à natureza do algoritmo de não melhorar a cada passo o atual melhor vetor parâmetro. Comumente muitas iterações são requeridas.
A característica de tamanho específica do minimizador é calculada como a
distância média do centro geométrico do simplex a todos os seus
vértices. Esse tamanho pode ser usado como um critério de parada, como o
simplex contrair a sí mesmo próximo do valor mínimo. O tamanho é retornado pela
função gsl_multimin_fminimizer_size.
A versão nmsimplex2 desse redutor ao mínimo é uma nova implementação de
operações O(N) das anteriores operações O(N^2) do redutor ao mínimo
nmsimplex. Usa o mesmo algoritmo básico, mas as atualizações do
simplex são calculadas mais eficientemente para problemas envolvendo dimensões maiores.
Adicionalmente, o tamanho do simplex é calculado como a distância
RMS (73)a
cad vértice a partir do centro ao invés de a distância média,
permitindo uma atualização linear dessa quantidade a cada passo. O uso de memória é
O(N^2) para ambos os algoritmos.
Esse método é uma variante do nmsimplex2 que inicializa o
simplex em torno do ponto de partida x usando um conjunto
aleatóriamente orientado de vetores base ao invés dos eixos coordenados fixos. As
dimensões finais do simplex são ajustadas de forma proporcional ao longo dos eixos coordenados pelo
vetor step_size. A aleatoriedade usa um gerador simples
determinístico de forma que chamadas repetidas a gsl_multimin_fminimizer_set para
um dado objeto resolvedor irá variar a orientação de uma forma bem definida.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse programa exemplo econtra o mínimo da função parabolóide definida anteiormente. A localização do mínimo é a uma certa distância inicial - offset - a partir da orígem em x e y, e o valor da função no mínimo é diferente de zero. O programa principal é dado abaixo, requer a função exemplo dada anteriormente nesse capítulo.
int
main (void)
{
size_t iter = 0;
int status;
const gsl_multimin_fdfminimizer_type *T;
gsl_multimin_fdfminimizer *s;
/* Position of the minimum (1,2), scale factors
10,20, height 30. */
double par[5] = { 1.0, 2.0, 10.0, 20.0, 30.0 };
gsl_vector *x;
gsl_multimin_function_fdf my_func;
my_func.n = 2;
my_func.f = my_f;
my_func.df = my_df;
my_func.fdf = my_fdf;
my_func.params = par;
/* Starting point, x = (5,7) */
x = gsl_vector_alloc (2);
gsl_vector_set (x, 0, 5.0);
gsl_vector_set (x, 1, 7.0);
T = gsl_multimin_fdfminimizer_conjugate_fr;
s = gsl_multimin_fdfminimizer_alloc (T, 2);
gsl_multimin_fdfminimizer_set (s, &my_func, x, 0.01, 1e-4);
do
{
iter++;
status = gsl_multimin_fdfminimizer_iterate (s);
if (status)
break;
status = gsl_multimin_test_gradient (s->gradient, 1e-3);
if (status == GSL_SUCCESS)
printf ("Minimum found at:\n");
printf ("%5d %.5f %.5f %10.5f\n", iter,
gsl_vector_get (s->x, 0),
gsl_vector_get (s->x, 1),
s->f);
}
while (status == GSL_CONTINUE && iter < 100);
gsl_multimin_fdfminimizer_free (s);
gsl_vector_free (x);
return 0;
}
O tamanho de passo inicial é escolhidos como 0.01, uma estimativa conservadora nesse caso, e o parâmetro minimizador de linha é ajustado em 0.0001. O programa termina quando o módulo do coeficiente angular tiver sido reduzido abaixo de 0.001. A saída do programa é mostrada abaixo,
x y f
1 4.99629 6.99072 687.84780
2 4.98886 6.97215 683.55456
3 4.97400 6.93501 675.01278
4 4.94429 6.86073 658.10798
5 4.88487 6.71217 625.01340
6 4.76602 6.41506 561.68440
7 4.52833 5.82083 446.46694
8 4.05295 4.63238 261.79422
9 3.10219 2.25548 75.49762
10 2.85185 1.62963 67.03704
11 2.19088 1.76182 45.31640
12 0.86892 2.02622 30.18555
Minimum found at:
13 1.00000 2.00000 30.00000
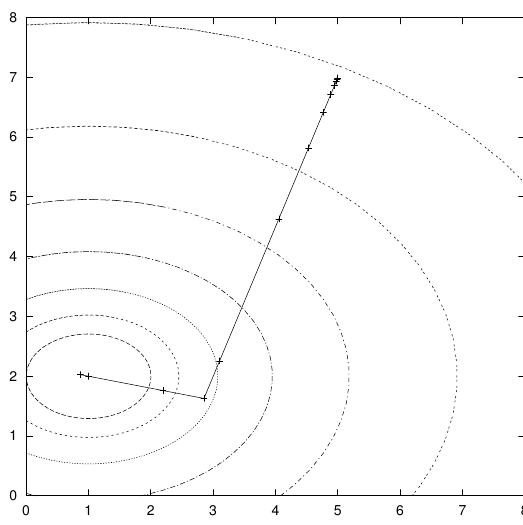
Note que o algoritmo gradualmente aumenta o tamanho do passo da mesma forma que sucessivamente move-o morro abaixo, como pode ser visto colocando em um gráfico os pontos sucessivos.

O algoritmo do coeficiente angular conjugado encontra o mínimo sobre sua segunda direção pelo fato de a fução ser puramente quadrática. Iterações adicionais podem ser necessárias para uma função mais complicada.
Aqui está outro exemplo usando o algoritmo Simplex de Nelder-Mead para minimizar a mesma função objeto exemplo, como acima.
int
main(void)
{
double par[5] = {1.0, 2.0, 10.0, 20.0, 30.0};
const gsl_multimin_fminimizer_type *T =
gsl_multimin_fminimizer_nmsimplex2;
gsl_multimin_fminimizer *s = NULL;
gsl_vector *ss, *x;
gsl_multimin_function minex_func;
size_t iter = 0;
int status;
double size;
/* Starting point */
x = gsl_vector_alloc (2);
gsl_vector_set (x, 0, 5.0);
gsl_vector_set (x, 1, 7.0);
/* Set initial step sizes to 1 */
ss = gsl_vector_alloc (2);
gsl_vector_set_all (ss, 1.0);
/* Initialize method and iterate */
minex_func.n = 2;
minex_func.f = my_f;
minex_func.params = par;
s = gsl_multimin_fminimizer_alloc (T, 2);
gsl_multimin_fminimizer_set (s, &minex_func, x, ss);
do
{
iter++;
status = gsl_multimin_fminimizer_iterate(s);
if (status)
break;
size = gsl_multimin_fminimizer_size (s);
status = gsl_multimin_test_size (size, 1e-2);
if (status == GSL_SUCCESS)
{
printf ("converged to minimum at\n");
}
printf ("%5d %10.3e %10.3e f() = %7.3f size = %.3f\n",
iter,
gsl_vector_get (s->x, 0),
gsl_vector_get (s->x, 1),
s->fval, size);
}
while (status == GSL_CONTINUE && iter < 100);
gsl_vector_free(x);
gsl_vector_free(ss);
gsl_multimin_fminimizer_free (s);
return status;
}
A busca do mínimo pára quando o tamanho do Simplex cai para 0.01. A saída é mostrada abaixo.
1 6.500e+00 5.000e+00 f() = 512.500 size = 1.130
2 5.250e+00 4.000e+00 f() = 290.625 size = 1.409
3 5.250e+00 4.000e+00 f() = 290.625 size = 1.409
4 5.500e+00 1.000e+00 f() = 252.500 size = 1.409
5 2.625e+00 3.500e+00 f() = 101.406 size = 1.847
6 2.625e+00 3.500e+00 f() = 101.406 size = 1.847
7 0.000e+00 3.000e+00 f() = 60.000 size = 1.847
8 2.094e+00 1.875e+00 f() = 42.275 size = 1.321
9 2.578e-01 1.906e+00 f() = 35.684 size = 1.069
10 5.879e-01 2.445e+00 f() = 35.664 size = 0.841
11 1.258e+00 2.025e+00 f() = 30.680 size = 0.476
12 1.258e+00 2.025e+00 f() = 30.680 size = 0.367
13 1.093e+00 1.849e+00 f() = 30.539 size = 0.300
14 8.830e-01 2.004e+00 f() = 30.137 size = 0.172
15 8.830e-01 2.004e+00 f() = 30.137 size = 0.126
16 9.582e-01 2.060e+00 f() = 30.090 size = 0.106
17 1.022e+00 2.004e+00 f() = 30.005 size = 0.063
18 1.022e+00 2.004e+00 f() = 30.005 size = 0.043
19 1.022e+00 2.004e+00 f() = 30.005 size = 0.043
20 1.022e+00 2.004e+00 f() = 30.005 size = 0.027
21 1.022e+00 2.004e+00 f() = 30.005 size = 0.022
22 9.920e-01 1.997e+00 f() = 30.001 size = 0.016
23 9.920e-01 1.997e+00 f() = 30.001 size = 0.013
converged to minimum at
24 9.920e-01 1.997e+00 f() = 30.001 size = 0.008
O tamanho do simplex primeiro aumenta, enquanto o simples move-se para adiante do mínimo. Após um momento o tamanho do simplex começa a decrescer pelo fato de o simplex se contrair em torno do mínimo.
| [ << ] | [ < ] | [ Acima ] | [ > ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Os métodos do coeficiente angular conjugado e BFGS são descritos em detalhes no seguinte livro,
Uma breve descrição de algoritmos de minimização multidimensional e referências mais recentes podem ser encontradas em,
O algoritmo simples é descrito no seguinte artigo,
| [ << ] | [ >> ] | [Topo] | [Conteúdo] | [Índice] | [ ? ] |
Esse documento foi gerado em 23 de Julho de 2013 usando texi2html 5.0.